- •Министерство образования и науки республики казахстан казахский агротехнический университет им. С. Сейфуллина
- •Учебно-методический комплекс для специальности
- •5В012000 «профессиональное обучение»
- •Предисловие
- •Распределение учебного времени
- •5. Краткое описание курса
- •5.1 Цели изучения курса оенд:
- •5.2 Задачи изучения курса:
- •6. Содержание курса
- •6.1 Перечень лекционных занятий
- •8. Список литературы Основная литература
- •Дополнительная литература
- •9. Политика курса
- •10. Информация об оценке знаний
- •Политика выставления оценок
- •Шкала оценки знаний студентов
- •Тема 1. Элементы кинематики
- •Тема 2. Динамика частиц
- •Тема 3. Работа и энергия
- •Тема 4. Твердое тело в механике
- •Тема 5. Физика колебаний
- •Тема 6. Молекулярно - кинетическая теория идеального газа
- •Тема 7. Основы термодинамики
- •Тема 8. Электростатика
- •Тема 9. Постоянный электрический ток
- •Тема 10. Магнитное поле в вакууме и в веществе
- •Тема 11. Явление электромагнитной индукции
- •Тема 12. Основы теории Максвелла для электромагнитного поля
- •Тема 13. Волновая оптика
- •Тема 14. Квантовая природа излучения
- •Тема 15. Элементы квантовой физики атомов
- •Элементы физики атомного ядра и элементарных частиц
- •Изучение движения тел по наклонной плоскости
- •Порядок работы
- •Контрольные вопросы
- •Изучение собственных колебаний пружинного маятника
- •Натуральный логарифм этого отношения называется логарифмическим декрементом затухания:
- •Порядок работы
- •Контрольные вопросы
- •Определение момента инерции маятника максвелла
- •На маятник действуют две силы: сила тяжести ft, направленная вертикально вниз и сила упругости двух нитей 2т (рис.2).
- •Порядок работы
- •Определение коэффициента вязкости жидкости методом стокса
- •Порядок работы
- •Определение отношения удельных теплоемкостей газа методом адиабатического расширения
- •1.Электроизмерительные приборы и их классификация
- •1.2. Классификация приборов по принципу действия
- •1.3.Характеристики электроизмерительных приборов
- •1.4.Амперметры, вольтметры, гальванометры
- •1.5.Вспомогательные электрические приборы
- •2. Правила работы с электрическими схемами
- •Для соблюдения техники безопасности при работе с электрическими схемами следует:
- •3.Измерения и обработка результатов измерений
- •Контрольные вопросы
- •Определение сопротивления проводников с помощью мостиковой схемы
- •Порядок работы
- •Контрольные вопросы
- •Лабораторная работа № 28 определение горизонтальной составляющей напряженности магнитного поля земли
- •Контрольные вопросы
- •Исследование процесса разряда конденсатора через сопротивление
- •Лабораторная работа № 41 определение длины световой волны с помощью дифракционной решетки
- •Лабораторная работа № 44 изучение поляризации света
- •Снятие вольтамперной характеристики фотоэлемента
- •Зависимость силы тока от прило-
- •Задачи для самостоятельной работы
- •Вопросы экзаменационных тестов Механика
- •Колебания и волны
- •Молекулярная физика и термодинамика
- •Электростатика
- •Постоянный электрический ток
- •Электромагнетизм
- •Оптика и квантовая физика
- •Основная литература
- •Дополнительная литература
- •1. Основные физические постоянные (округленные значения)
- •2. Плотность твердых тел
- •3. Некоторые свойства твердых веществ
- •4. Плотность жидкостей
- •5. Некоторые свойства жидкостей
- •6. Плотность газов (при нормальных условиях)
- •Алия Кенжебековна Мукашева
Тема 7. Основы термодинамики
I закон термодинамики известен со школьного курса физики
Q = U + A - I закон термодинамики или закон сохране -
ния и превращения энергии в термодинамике.
Теплота, сообщаемая системе, расходуется на изменение внутренней энергии и на совершение работы против внешних сил.
В дифференциальной форме:
dQ = dU + dA
В более корректной форме:
Q = dU + A
dU – бесконечно малое изменение внутренней энергии
A – элементарная работа
Q – бесконечно малое количество теплоты
dU является полным дифференциалом, а A и Q – таковыми не являются.
Внутренняя энергия – важная характеристика термодинамической системы – энергия движения и взаимодействия частиц, из которых состоит тело
U = Eк + Ep
Для идеального газа Ер = 0, тогда U = Eк или
![]()
![]()
Работа, совершаемая, газом при изменении объема определяется по формуле
|
δA = pdV
П |
Полная работа определяется площадью, ограниченной осью абсцисс.
В термодинамике для характеристики тепловых свойств тел используется понятие теплоемкости.
Известно, теплота Q, переданная или отданная телом определяется по формуле
![]()
![]() Q
= mcT
где с – удельная теплоемкость
Q
= mcT
где с – удельная теплоемкость
-
- теплота, необходимая для нагревания вещества массой 1 кг на 1 К.
Помимо удельной теплоемкости часто целесообразно использовать молярную теплоемкость
![]()
![]() -
теплота,
необходимая для нагревания
-
теплота,
необходимая для нагревания
1 моля вещества на 1 К.
Удельная теплоемкость связана с молярной теплоемкостью соотношением:
С = с
Различают теплоемкости при V = const и p = const
![]()
![]()
![]() -
уравнение
Майера
-
уравнение
Майера
показывает, что Ср > CV на R.. Это объясняется тем, что при нагревании газа при p = const требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.
При рассмотрении термодинамических процессов важно знать характерное для каждого газа отношение Ср /СV
![]()
где i - число степеней свободы.
Адиабатный процесс – процесс, протекающий без теплообмена с окружающей средой - Q = 0 – все быстропротекающие процессы.
Адиабатные процессы применяются в двигателях внутреннего сгорания (расширение и сжатие горючей смеси в цилиндрах); процесс распространения звука в среде.
 р
Адиабатный процесс описывается
р
Адиабатный процесс описывается
уравнением Пуассона
-адиабата pV = const
-изотерма где - показатель адиабаты.
V
Рассмотренные изохорный, изобарный, изотермический и адиабатный процессы имеют общую особенность – происходят при постоянной теплоемкости.
Процесс, в котором теплоемкость остается постоянной называется политропным.
Уравнение политропы pV n = const
![]()
где - показатель политропы
Очевидно, что при С = 0, n = - уравнение адиабаты
при С = , n = 1 - уравнение изотермы
при С = Ср, n = 0 - уравнение изобары
при С = СV n = , - уравнение изохоры
Таким образом, все рассмотренные процессы являются частными случаями политропного процесса.
Рассмотрим применение I закона термодинамики к различным процессам:
1. Т = const – изотермический процесс dU = 0; Q = A
В![]() ся
теплота, сообщаемая газу, расходуется
на совершение им работы против внешних
сил
ся
теплота, сообщаемая газу, расходуется
на совершение им работы против внешних
сил
2. p = const – изобарный процесс Q = dU + A


![]()
![]()
![]()
![]()
Тогда - работа газа при изобарном процессе
Отсюда физический смысл газовой постоянной R: Т2 –Т1 = 1К, то для 1 моля газа R = A, т.е. R численно равно работе изобарного расширения 1 моля идеального газа при нагревании его на 1К.
В![]()
![]() изобарном процессе при сообщении газу
массой m
количества теплоты его внутренняя
энергия возрастает на величину
изобарном процессе при сообщении газу
массой m
количества теплоты его внутренняя
энергия возрастает на величину
При этом газ совершает работу
3. V = const - изохорный процесс
Г![]() аз
не совершает работы над внешними силами
аз
не совершает работы над внешними силами
![]()
4. Q = 0 – адиабатный процесс

Тогда A = - dU т.е. внешняя работа совершается за счет изменения внутренней энергии.
Круговой процесс – процесс, при котором система, пройдя через ряд состоя-ний, возвращается в исходное состояние.
 p
p
1 1 – a – 2 – расширение газа
b
а 2 – b – 1 – сжатие газа
2
V
V 1 V2
Работа, совершаемая газом за цикл, определяется площадью охватываемой замкнутой кривой.
Если круговой процесс идет по часовой стрелке, то работа будет положительной - прямой цикл, если же против часовой стрелки, то работа отрицательна – обратный цикл.
Прямой цикл используется в тепловых двигателях – совершающих работу за счет полученной извне теплоты. Обратный цикл используется в холодильных машинах – в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой.
В результате кругового процесса система возвращается в исходное состояние и U = 0. И тогда I закон термодинамики Q = A, т.е. работа, совершаемая за цикл, равна количеству тепла, полученной извне.
Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому Q = Q1 – Q2
где Q1 – тепло полученное системой Q2 - тепло отданное системой.
П![]() оэтому
оэтому
- к.п.д. для кругового процесса.
Процесс, который может самопроизвольно протекать как в прямом, так и в обратном направлениях называется обратимым. Примером обратимого процесса могло бы служить колебание маятника, если бы оно происходило без трения. Все механические процессы, происходящие, без трения были бы обратимые, однако трение не устранимо.
Необратимым называется процесс, который нельзя провести в обратном направлении через те же промежуточные состояния: сжатие и расширение газа, диффузия газов.
Энтропия наряду с энергией является важной характеристикой состояния термодинамической системы. Энтропия является величиной, с помощью которой учитывают потери и рассеяние теплоты, происходящие в реальных процессах, превращение теплоты в другие виды энергии при теплообмене.
Но чаще интересует изменение энтропии так как оно определяет обратимость или необратимость процессов в изолированной системе.
![]()
![]()
Для обратимых процессов изменение энтропии S = 0
Для необратимых процессов S > 0, т.е. энтропия системы возрастает.
Энтропия - определяет только состояние системы и не зависит от пути, каким система пришла в это состояние.
I закон термодинамики устанавливает количественное соотношение при превращении теплоты в механическую работу.
II закон термодинамики определяет направление развития процессов: естественные процессы протекают в сторону увеличения энтропии. Наиболее общее выражение II закона термодинамики: в изолированной системе при всех реальных процессах энтропия возрастает, или невозможен процесс, единственным результатом которого является превращение в работу теплоты, взятой от нагревателя, т.е.
A < Q1 - II закон термодинамики
Таким образом, тепловая машина должна работать по схеме:
-
Нагреватель
Т1
 Q1
Q1
Рабочее тело |
Q2
-
Холодильник
Т2
II закон термодинамики доказывает невозможность создания вечного двигателя.
Основываясь на II закон термодинамики, и анализируя работу тепловых двигателей, французский инженер Карно пришел к выводу, что наивыгоднейшим круговым процессом является обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов, так как он характеризуется наибольшим к.п.д. Такой цикл и получил название цикла Карно. Процесс протекает в идеальной тепловой машине – машине, которая действует без трения, т.е. без необратимых потерь.
|
1 - 2; 3 – 4 – изотермы 2 – 3; 4 – 1 – адиабаты
- к.п.д. идеальной тепловой машины, работающей по циклу Карно |
Таким образом, для цикла Карно к.п.д. определяется только температурами нагревателя и холодильника и не зависит от состава рабочего тела.
Реальный газ – газ, где учитываются объем (размеры) и силы взаимодействия молекул. Учитывая собственный объем молекул и силы межмолекулярного взаимодействия, голландский физик И.Ван-дер-Ваальс введя поправки в уравнение Менделеева-Клайперона, вывел уравнение состояния реального газа.
Уравнение состояния для 1 моля идеального газа имеет вид pV = RT
Согласно
этой формуле объем газа при сжатии может
стать равным нулю. В случае реальных
газов часть объема занята самими
молекулами. Поэтому объем, занимаемый
газом, должен быть уменьшен на величину
b,
где b-
объем занимаемый самими молекулами,
т.е. (V-b).
Таким
образом, b
–постоянная величина, учитывающая
объемы (размеры) молекул.В![]() реальных газах имеются силы взаимного
притяжения молекул, которые действуют
дополнительно к силам внешнего давления
и как бы сжимают газ. Вследствие этого
возникает добавочное внутреннее давление
pi,
т.е.
реальных газах имеются силы взаимного
притяжения молекул, которые действуют
дополнительно к силам внешнего давления
и как бы сжимают газ. Вследствие этого
возникает добавочное внутреннее давление
pi,
т.е.
где (p + pi), а – постоянная величина, учитывающая
силы межмолекулярного притяжения
Т![]() огда,
введя поправки на V
и p,
получим уравнение состояния реального
газа
огда,
введя поправки на V
и p,
получим уравнение состояния реального
газа
- уравнение Ван-дер-Ваальса для 1 моля газа
Величины a и b для различных газов различны и их значение приводятся в справочных таблицах.
Д![]() ля
любой массы газа
ля
любой массы газа
Уравнение Ван-дер-Ваальса не единственное уравнение, описывающее реальные газы. Существуют и другие уравнения, некоторые из них даже точнее описывают реальные газы, но не рассматриваются из-за их сложности.
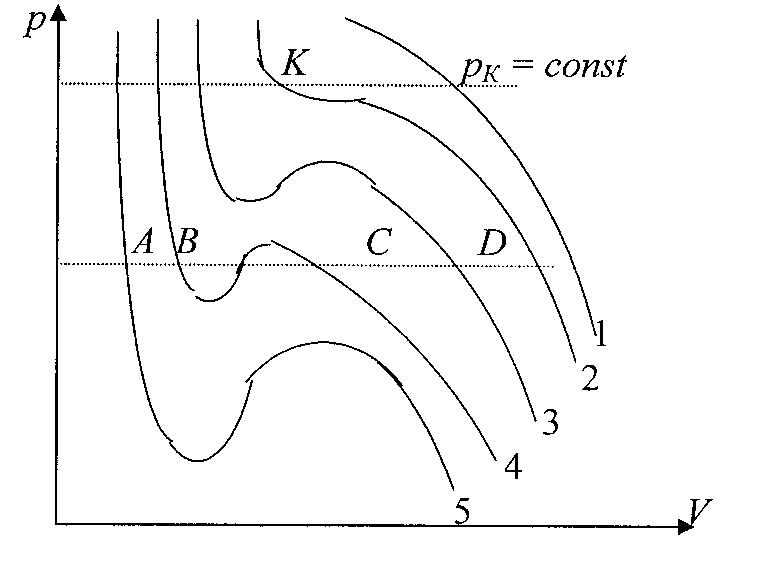
Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса – кривые зависимости давления p от объема V при заданных температурах Т, определяемые уравнение Ван-дер-Ваальса для 1 моля газа.
Эти кривые рассматриваются для четырех различных температур и имеют своеобразный характер.
|
Задавая различные температуры T1 > T2 > T3 > T4 > T5 получим семейство изотерм Ван-дер-Ваальса. При высоких температурах изотерма реального газа отличается от изотермы идеального газа только некоторым искажением формы. Изобара AD пересекает изотерму в одной точке. Это означает, что каждому значению давления и температуры |
соответствует единственное значение объема, т.е. при высоких температурах вещество находится в однофазном – газообразном состоянии. Невысоким температурам соответствуют изотермы 2-, 3-, 4, на которых имеются изгибы.
Изобара AD пересекает изотерму 4 в трех точках А, В, С. Это означает, что вещество одновременно находится в трех фазовых состояниях. Переход от изотермы 5 к изотермам 4,3,2,1, соответствующий повышению температуры, приводит к тому, что изгибы на изотермах сглаживаются. Расстояние между точками А и С уменьшаются и на изотерме 2 сливаются в одну точку К. Здесь рК = const является касательной к изотерме. Эта изотерма называется критической, соответствующая температура Тк – критической , точка К – критической. Соответствующие этой точке VK и рК – называются критическими.
Состояние с критическими параметрами (VK,,рК,,ТК) называются критическим состоянием.
Температурам, выше критическим соответствует только газообразное состояние вещества. Следовательно, критическая температура ТК – это наивысшая температура, при которой газ может еще может быть превращен в жидкость. При критическом состоянии вещества различия в свойствах пара и жидкости отсутствуют. Критические состояния характеризуется непрерывным переходом пара в жидкость и жидкости в пар.
Мы знаем, что U = U1 + U2 = Eк + Eр.
В![]() случае реального газа, помимо кинетической
энергии Ек
нужно
учитывать потенциальную энергию Ер
взаимодействия молекул.
случае реального газа, помимо кинетической
энергии Ек
нужно
учитывать потенциальную энергию Ер
взаимодействия молекул.
В нутренняя энергия для 1 моля идеального газа
Т![]() ак
как , то
ак
как , то
Работа сил молекулярного сцепления равна: dA = pi dV,
![]()
Мы знаем, что
Тогда dU которое произошло за счет совершения работы
![]() или
интегрируя, получим:
или
интегрируя, получим:
![]()
- потенциальная энергия
![]()
Тогда - внутренняя энергия 1 моля реального газа.
Следовательно, внутренняя энергия реального газа зависит как от температуры, так и от его объема.
В термодинамически неравновесных системах возникают особые необратимые процессы – явления переноса – в результате которых происходит пространственный перенос энергии, массы, импульса.
К явлениям переноса относятся:
1. Теплопроводность обусловлена переносом энергии (горячий чай – холодная ложка). Если в одной области Ек молекул больше, чем в другой, то в процессе столкновений молекул с течением времени происходит выравнивание кинетической энергии, т.е. температур.
Перенос
энергии в форме теплоты подчиняется
закону Фурье
![]()
jE – плотность теплового потока – энергия, переносимая в форме теплоты через единицу площади в единицу времени, перпендикулярную оси х.
![]() -
коэффициент теплопроводности
-
коэффициент теплопроводности
![]()
![]() – градиент
температуры
– изменение температуры на единицу
длины. «-» - при теплопроводности энергия
переносится в направлении убывания
температуры.
– градиент
температуры
– изменение температуры на единицу
длины. «-» - при теплопроводности энергия
переносится в направлении убывания
температуры.
2. Диффузия - самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и твердых тел.
Явление диффузии подчиняется закону Фика
![]()
jm – плотность потока массы – масса вещества, диффундирующего в единицу времени через единицу площади, перпендикулярную оси х
D – коэффициент диффузии
![]() -
градиент плотности, «-» показывает,
что перенос массы происходит в направлении
убывания плотности.
-
градиент плотности, «-» показывает,
что перенос массы происходит в направлении
убывания плотности.
Согласно
кинетической теории газов
![]()
3. Внутреннее трение (вязкость). Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, а движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Сила трения между слоями подчиняется закону Ньютона
![]()
Тогда
от одного слоя к другому передается
импульс, по модулю равный действующей
силе
![]()
jp – плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х.
![]() -
градиент скорости, «-» - указывает, что
импульс переносится в направлении
убывания скорости.
-
градиент скорости, «-» - указывает, что
импульс переносится в направлении
убывания скорости.
Динамическая вязкость определяется по формуле
![]()
Коэффициенты переноса связаны между собой соотношениями
![]() и
и
![]()


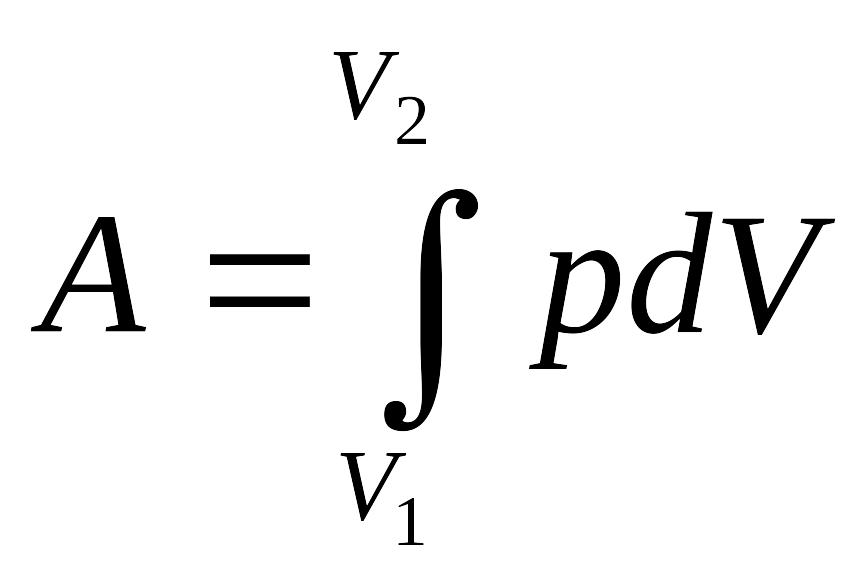 олная
работа, совершаемая газом при изменении
объема от V1
до V2
определим
интегрированием
олная
работа, совершаемая газом при изменении
объема от V1
до V2
определим
интегрированием