Работа 1 Рентгеноструктурный анализ

Работа 2 Определение параметров полупроводников

Цель научиться определять удельное сопротивление полупроводников, диффузную длину пробега основных носителей заряда и время их жизни.

Оборудование: измерительный усилитель У2-6, гальванометр М195/2, миллиамперметр, блок питания, фокусирующая линза, источник света, модулятор, образцы полупроводников, препаратоводитель.

Краткое теоретическое обоснование

Равновесные и неравновесные носители заряда в полупроводниках

Известно, что в полупроводниках непрерывно протекают встречные процессы генерации (возникновения) и рекомбинации (исчезновения) подвижных носителей заряда (электронов и дырок), обусловленные ионизацией атомов основного вещества и примесных центров, а также структурных дефектов (рис. 2.1). Назовем скоростями генерации ( , ) и рекомбинации ( , ) числа электронов или дырок, генерируемых и, соответственно, рекомбинирующих в единице объема полупроводника за единицу времени.

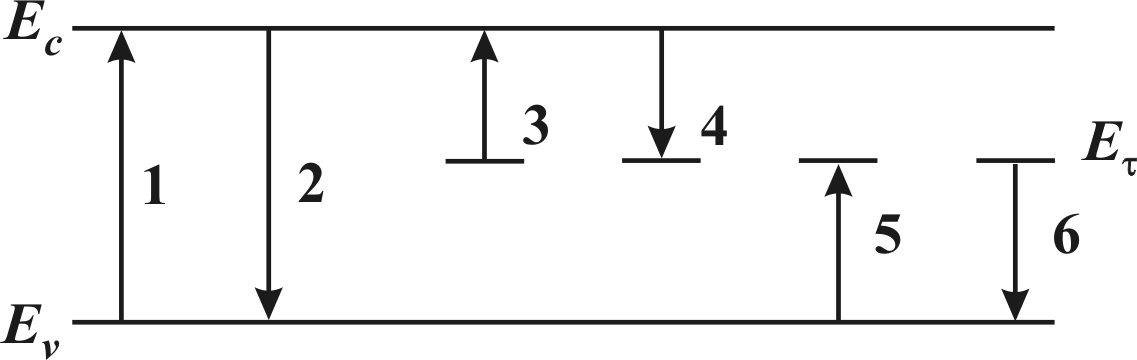
Рис. 2.1. Энергетическая схема генерации и рекомбинации электронов и дырок в полупроводнике: Е_c — дно зоны проводимости; Е_v — верх валентной зоны; Е_τ — энергетический уровень электрона, связанного с центром захвата; 1 — генерация электронно-дырочной пары; 2 — межзонная рекомбинация электрона и дырки; 3 — эмиссия электрона с уровня Е_τ; 4 — захват свободного электрона на уровень Е_τ; 5 — захват связанного электрона (эмиссия дырки); 6 — переход электрона с уровня Е_τ в валентную зону (захват дырки)

В условиях термодинамического равновесия (без внешних энергетических воздействий) подвижные носители заряда создаются (генерируются) только в результате термической ионизации. При этом процессы генерации и рекомбинации уравновешивают друг друга: , (нулевой индекс означает состояние термодинамического равновесия). Обозначим , — равновесные концентрации электронов и дырок; они постоянны во времени и определяются видом полупроводника, составом примесей, температурой и т. д.

Термодинамическое равновесие может быть нарушено таким внешним энергетическим воздействием, которое вызывает дополнительную к тепловой ионизации генерацию электронов и дырок: , . Тогда и концентрация электронов и дырок увеличится и составит

для электронов ,

для дырок

Избыточные (сверх равновесных) концентрации и называют еще концентрациями неравновесных носителей заряда (соответственно электронов и дырок). Увеличение числа подвижных носителей заряда повышает вероятность их рекомбинации, поэтому скорости рекомбинации возрастают в сравнении со скоростями рекомбинации при равновесии: , . Величины и — скорости рекомбинации неравновесных электронов и дырок. Они зависят от избыточных концентраций и и по определению равны нулю при и . Разложив эти зависимости в степенной ряд и сохранив для достаточно малых и только линейные члены, получим

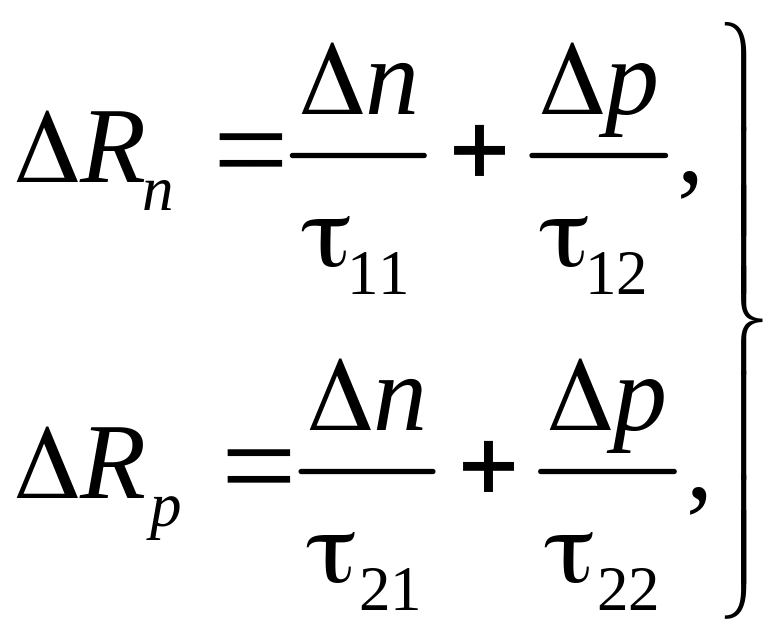(1)

где , , , — постоянные для данного кристалла величины, имеющие размерность времени. Для выполнения (1) обычно достаточно, чтобы концентрация неравновесных пар была малой по сравнению с концентрацией равновесных носителей заряда, т. е.

. (2)

Во многих полупроводниках (в том числе и в германие) рекомбинация носителей заряда происходит исключительно с помощью поочередного захвата электронов и дырок на примесные центры или структурные дефекты. Непосредственная рекомбинация электронов и дырок (переходы типа 2, рис. 2.1) практически отсутствуют. В этом случае скорость рекомбинации носителей одного знака обычно слабо зависит от концентрации носителей другого знака. Поэтому равенство (1) можно записать в виде:

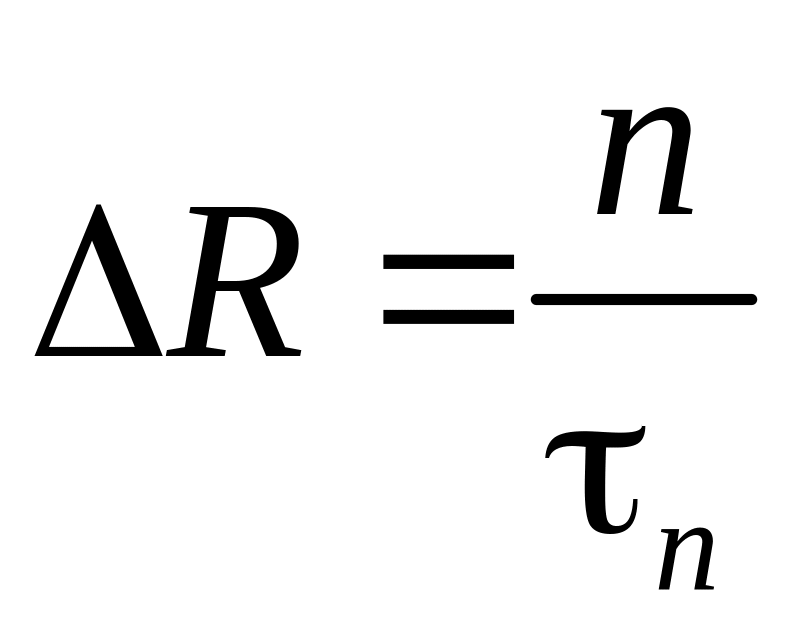, . (3)

Далее будем рассматривать только такие процессы избыточной (по отношению к тепловой) генерации, когда ионизируются только атомы основного вещества полупроводника, а не примесей. При этом возникают одновременно электроны и дырки ( ). На энергетической диаграмме такой процесс изображается как возбуждение электрона с валентной зоной в зону проводимости (рис. 2.1, переход 1). Например, он происходит при поглощении света с энергией квантов, большей, чем ширина запрещенной зоны. Анализ для германия при комнатной температуре показывает, что в условиях одновременной попарной генерации неравновесных электронов и дырок и соблюдения условия (2) состояние ионизации примесей и дефектов обычно остается практически таким же, как и при равновесии. Но если число ионизированных примесных центров в полупроводнике при возбуждении не изменяется, то в условиях сохранения электронной нейтральности концентрации неравновесных электронов и дырок должны быть равны:

. (4)

Следовательно, и скорости рекомбинации неравновесных электронов и дырок одинаковы ( ), иначе бы при одинаковой скорости генерации ( ) равенство (4) невозможно. Отсюда из (3) следует, что

и . (5)

Постоянная величина представляет собой среднестатистическое время существования неравновесных свободных электронов и дырок от момента генерации до рекомбинации (время жизни неравновесных носителей) и является одним из основных параметров, характеризующих рекомбинационные свойства полупроводника. Время жизни в различных полупроводниках и при различных условиях может принимать значения от 10^–10 до 10^–3 с.

Диффузия и дрейф неравновесных носителей заряда

В неоднородном полупроводнике, в котором концентрация электронов и дырок изменяется от точки к точке (является функцией координаты x), должен возникнуть диффузионный ток электронов и дырок. Поток электронов , возникающий в результате диффузии в направлении x, пропорционален градиенту концентрации электронов в этом направлении и определяется уравнением вида

. (6)

Аналогично выражение для диффузионного потока дырок:

, (7)

где и — коэффициенты диффузии, имеющие размерность [см²/с]. Диффузионным потокам носителей соответствуют диффузионные токи электронов и дырок и , возникновение которых приводит к возникновению пространственных зарядов и электростатических полей, препятствующих протеканию диффузионных токов. Поскольку электрическое поле Е создает дрейфовые токи электронов и дырок, то полный электронный и дырочный токи равняются сумме диффузионных и дрейфовых токов:

, (8)

, (9)

где и — подвижности электронов и дырок (размерность [см²/(В·с)]). Таким образом, плотность общего тока ј определяется уравнением

. (10)

Очевидно, что в состоянии термодинамического равновесия .

Если электроны и дырки в полупроводнике описываются статистикой Больцмана (это справедливо для германия с концентрациями n,  см^–3 при комнатной температуре), то коэффициенты диффузии и подвижности связаны между собой соотношением Эйнштейна:

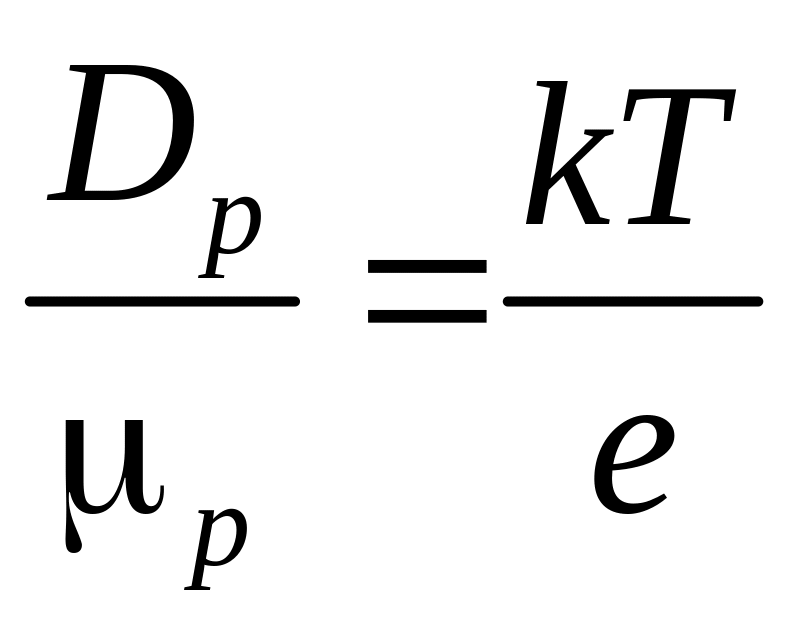, , (11)

где k — постоянная Больцмана.

Рассмотрим особенности диффузии и дрейфа неравновесных носителей заряда в однородных полупроводниках. Пусть в однородном полупроводнике существует неоднородное распределение носителей заряда и , вызванное, например, локальным освещением образца. В этом случае (как и для неоднородного полупроводника) возникнут диффузионные и дрейфовые токи электронов и дырок, которые описываются уравнениями (8), (9), (10). Из этих уравнений видно, что при отсутствии электрического тока электростатическое поле Е, возникшее в результате диффузии, будет меньше, чем больше равновесные концентрации и , так как дрейфовый ток создается и электронами, и дырками. Таким образом, если электропроводность полупроводника достаточно велика и концентрации неравновесных носителей заряда и значительно меньше концентрации равновесных носителей заряда ( , ), то в первом приближении можно считать, что электрическое поле отсутствует и имеет место условие электронейтральности . Это означает, что процесс диффузии электронов и дырок происходит свободно как диффузия неравновесных нейтральных пар электрон — дырка. Если теперь к образцу, в котором созданы неравновесные пары электрон — дырка, приложить внешнее электрическое поле, то они будут дрейфовать в этом поле с постоянной скоростью. Очевидно, что совместная диффузия и дрейф электронов и дырок при условии электронейтральности характеризуется эффективной дрейфовой подвижностью и эффективным коэффициентом диффузии D, одинаковыми для электронов и дырок. Величины и D называют биполярной дрейфовой подвижностью и биполярным коэффициентом диффузии. Эти величины связаны с подвижностями и коэффициентами диффузии электронов и дырок следующими зависимостями:

, . (12)