Подготовка исследуемых образцов

Поликристаллические образцы изготовляются обычно в виде тонких цилиндриков или близких к ним по форме кусочков вещества диаметром 0,2 — 1,0 мм. В том случае, если нет возможности изготовить цилиндрические образцы, применяют плоские образцы. Способы изготовления цилиндрических образцов весьма многообразны. Например, наклеивают порошок исследуемого вещества с помощью коллодия, цапонлака или другой связки на стеклянную нить диаметром 0,01 — 0,1 мм; вытачивают образец из кусочка слитка на станке, используя кусочек тянутой проволоки. Так как в тянутой проволоке часто наблюдается преимущественная ориентация кристаллов (текстура), образец необходимо предварительно обжечь, чтобы перекристаллизовать его и разориентировать кристаллы. Из мягкого кристалла цилиндрические образцы можно изготовить путем обкатки. Исследуют цилиндрические образцы обычно «на просвет». Плоские образцы готовят путем нанесения слоя исследуемого вещества на подложку либо путем подготовки шлифа из кусочка или целого слитка. Плоские образцы исследуют, применяя съемку «на отражение».

Расшифровка рентгенограммы и расчеты

Расшифровку рентгенограммы разбивают на ряд последовательных этапов

Рис. 1.15. Схема рентгенограммы поликристаллического вещества

1. Оценка интенсивности линий. Сначала необходимо пронумеровать все линии рентгенограммы от 1 до 9 (рис. 1.15). Интенсивность линий оценивается по пятибалльной шкале. Самую яркую (черную) оценивают в 5 баллов, а самую слабую — 1 балл. Остальным линиям приписывают некоторые промежуточные значения интенсивности.

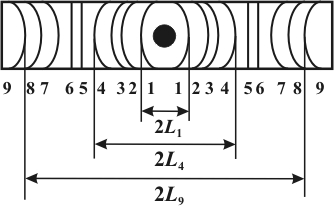
2. Промер рентгенограммы. Расстояние между симметричными относительно черного пятна линиями рентгенограммы измеряются штангенциркулем с точностью до десятых долей миллиметра.

3. Определение углов скольжения. Углы скольжения определяются по формуле (6), которую можно переписать в виде:

, (8)

где — коэффициент камеры.

В данной работе применяется стандартная камера РКД с диаметром  мм. В этом случае и численное значение угла скольжения в градусах будет равно численному значению половины расстояния 2L в миллиметрах, т. е.

 (мм)_. (9)

4. Введение поправки на толщину образца. Формула (9) справедлива, если образец помещен в центре цилиндрической камеры и «не имеет толщины». На самом деле образец не является бесконечно тонким. Рентгеновские лучи рассеиваются и поглощаются всем объемом образца. Но исследуемый образец может поглощать рентгеновские лучи настолько мощно, что в отбитом луче будет использоваться только внешняя поверхность. В этом случае расстояние между линиями на рентгенограмме будет больше, чем при отсутствии поглощения. Поэтому необходимо ввести поправку на поглощение. Если измерять 2L между серединами линий на рентгенограмме, то эта поправка будет равна:

,

где r — радиус образца в миллиметрах.

При измерении расстояния 2L между внешними краями линий поправка на поглощение равна диаметру образца

,

а настоящее значение 2L будет равно

.

Поэтому угол скольжения запишется в виде:

.

5. Определение . Используя микрокалькулятор, определите с точностью до трех знаков после запятой.

6. Определение серий, к которым принадлежат линии рентгенограммы. Так как съемка исследуемой рентгенограммы выполнена без селективного фильтра, то на ней присутствуют как линии -серии, так и линии -серии. Линии -серии на рентгенограмме располагаются ближе к первичному пучку (черному пятну) кроме того они менее интенсивны, чем -серии. Для того чтобы установить, какие линии рентгенограммы относятся к -серии, а какие к -серии, следует использовать отношение

.

Из этого следует: если для двух соседних линий отношение синуса более интенсивной линии к синусу менее интенсивной линии, лежащей ближе к черному пятну, равно приблизительно 1,1, то менее интенсивная линия относится к ‑серии, а более интенсивная к -серии. Определив четыре линии -серии, их необходимо исключить из расчетов. Все результаты измерений и вычислений запишите в таблицу 2.

Таблица 2

№ линий	Интенсивность линий	2L /мм/			*	-серия или -серия
1
2
...
9

7. Получение списка межплоскостных расстояний. Необходимо пронумеровать линии -серии и по формуле (4) Вульфа — Брэгга определить межплоскостные расстояния:

. (10)

Если считать, что все линии рентгенограммы первого порядка отражения, то и тогда

. (11)

Для рентгеновской трубки БСВ-Fe  нм и поэтому межплоскостные расстояния можно вычислить по формуле

. (12)

Результаты измерений запишите в таблицу 3.

Таблица 3

№ линии -серии			d /нм/	Вещество
1
2
3
4
5

Межплоскостные расстояния необходимо определять с точностью до тысячных долей нанометра. Каждое химическое соединение имеет свои определенные расстояния между атомными плоскостями. В природе не встречаются два разных химических соединения, у которых все межплоскостные расстояния и интенсивности линий были бы одинаковые. Можно сказать, что список межплоскостных расстояний любого химического соединения является как бы его паспортом. Поэтому, получив рентгенограмму какого-нибудь вещества и вычислив его межплоскостные расстояния, в соответствующем справочнике мы можем определить, какое это вещество. В таблице 4 приведен список межплоскостных расстояний для шести веществ (для упрощения задачи указаны только пять первых расстояний). Необходимо сравнить их со списком, который получился в результате вычислений, и определить, какое вещество сфотографировано на рентгенограмме. Если отличие между табличными и полученными значениями не превышает  0,002 нм для  нм и  0,001 нм для  нм, то исследуемое вещество можно считать определенным.

Таблица 4

, нм	Mg	Zn	Cu	Co	Ni	Fe
	0,210	0,247	0,209	0,204	0,203	0,201
	0,200	0,231	0,181	0,177	0,176	0,143
	0,190	0,209	0,128	0,125	0,125	0.117
	0,168	0,169	0,109	0,107	0,106	0,101
	0,127	0,134	0,104	0,102	0,102	0,090

8. Определение индексов плоскостей. Как известно, в кубической решетке постоянная а, межплоскостные расстояния d и индексы h, k, l связаны между собой уравнением

.

Отсюда следует, что для определения параметров кубической решетки необходимо знать индексы плоскостей, участвующих в отражении рентгеновских лучей. Для каждого кольца на рентгенограмме, полученного при отражении рентгеновских лучей от атомных плоскостей кристалла, можно записать:

;

………………………. ;

;

………………………..

Или исключив , получим

Но индексы (h, k, l) — числа только целые; а раз так, то в правой части должно получиться отношение целых чисел. Следовательно, необходимо вычислить для всех линий с точностью до тысячных долей. После этого необходимо вычислить следующие отношения синусов с точностью до сотых:

Получается ряд чисел. Если решетка вещества, сфотографированная на рентгенограмме, простая кубическая, то эти числа будут очень близки к целым (с точностью до 0,01). Например: 1,00 2,09 3,05 4,07 4,99 = 1 2 3 4 5.

Если же эти числа нельзя округлить до целых, то решетка не простая кубическая. Предположив, что решетка объемоцентрированная, необходимо умножить каждое число ряда на 2 и снова попробовать округлить до целых. Если же и умноженный на 2 ряд чисел нельзя округлить до целых, то следует предположить, что решетка гранецентрированная и умножить каждое число первого ряда на 3 и снова попробовать округлить полученные числа до целых. После того как тем или иным способом будет получен ряд округленных до целых значений чисел, каждое число из этого ряда необходимо представить в виде суммы трех простых чисел, которые и будут искомыми индексами. Значения h, k, l в зависимости от суммы их квадратов приведены в таблице 5.

Таблица 5

	1	2	3	4	5	6	7	8	9	10	11	12
h, k, l	001	011	111	002	012	112	нет	022	003 122	013	113	222

9. Определение типа решетки. Известно, что в решетках разного типа отражение наблюдается от различного сочетания атомных плоскостей. Существует общее правило для определения типа решетки

А. Если сумма квадратов индексов каждой отдельно взятой плоскости есть число четное, т. е. , то решетка объемоцентрированная.

Б. Если индексы h, k, l каждой отдельно взятой плоскости представляют собой числа с одинаковой четностью (ноль — четное число), то решетка гранецентрированная. Например, (1, 1, 1) (0, 0, 2) (3, 5, 7) и т. д.

В. Неподчинение первым двум правилам указывает на наличие примитивной кубической решетки.

10. Определение параметров решетки. Параметр или постоянную решетки а определяют 5 раз (для каждой линии) по формуле

.

Потом находят среднее арифметическое значение а. Результаты расчетов записывают в таблицу 6.

Таблица 6

№ линии ‑cерии					округл.		Тип решетки	h, k, l	a (нм)	(нм)	z
1
…
5

11. Определение числа частиц в элементарной ячейке. Если постоянная кубической решетки а, то ее объем , масса , где — плотность вещества. Обозначим массу одной частицы , тогда количество частиц в ячейке будет

.

Массу частицы можно определить по формуле

,

где M — молярная масса, — число Авогадро. Поэтому

. (13)