Дифракция рентгеновских лучей

Прохождение рентгеновских лучей через кристаллическое вещество сопровождается отклонением их от первоначального направления. Это явление, получившее название дифракции рентгеновских лучей, объясняется следующим образом. Под воздействием электромагнитного поля рентгеновских лучей электроны атомов, входящих в кристаллическую решетку вещества, начинают колебаться. Частота их вынужденных колебаний будет равна частоте электромагнитного поля первичного пучка рентгеновских лучей. В первом приближении сложную картину колебаний всех электронов, входящих в атом, допустимо заменить понятием «колеблющийся атом». Такой колеблющийся атом становится источником электромагнитных волн, распространяющихся от него во все стороны с частотой, равной частоте первичного пучка. А так как в кристаллической решетке положение атомов относительно друг друга одинаковое, то лучи, рассеянные отдельными атомами, интерферируют между собой. Интенсивность их в одном направлении будет получаться значительно большей, чем в других. Следовательно, кристалл для рентгеновских лучей является трехмерной дифракционной решеткой.

Уравнение Вульфа — Брэгга

а

б

Рис. 1.8. К выводу уравнения Вульфа — Брэгга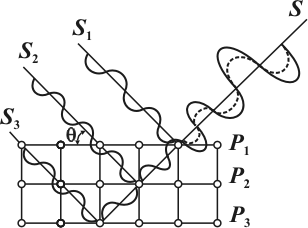

В 1913 году русский кристаллофизик Ю.В. Вульф и почти одновременно с ним английский физик В.Г. Брэгг дали простое и наглядное объяснение явления отклонения рентгеновских лучей при прохождении их через кристаллическое вещество. Они показали, что сложную картину рассеивания рентгеновских лучей атомами можно рассматривать как отражение рентгеновских лучей от параллельных атомных плоскостей кристалла.

Пусть на кристалл падает пучок монохроматических рентгеновских лучей под углом к одному из семейства атомных плоскостей (рис. 1.8, а). Луч , падая на атомную плоскость , отбивается от нее в направлении S. Второй луч , пройдя первую атомную плоскость (на основании свойств рентгеновских лучей проникать через вещество), отразится от плоскости и также выйдет в направлении S и т. д. Отраженные параллельными атомными плоскостями лучи будут интерферировать между собой и в зависимости от их фазового соотношения усиливать или ослаблять друг друга. Отсюда следует, что в направлении S интенсивность рентгеновских лучей будет максимальной, если лучи, отраженные отдельными атомными плоскостями, будут находиться в одной фазе. Или, иначе говоря, если разность их хода будет кратна длине волны.

Из рисунка 1.8, а видно, что фазовые отношения отраженных лучей будут зависеть от длины волны , межплоскостного расстояния d и угла скольжения . Угол скольжения является дополнением до 90° к углу отражения. Выразим эту зависимость математически.

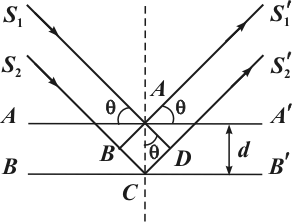
На рисунке 1.8, б показаны две соседние кристаллографические плоскости и . Абсолютный показатель преломления всех сред для рентгеновских лучей близок к единице. Поэтому оптическая разность хода  между двумя лучами и , отбивающихся от плоскостей и , запишется в виде формулы , где d — межплоскостное расстояние, — угол скольжения.

Если длина волны рентгеновских лучей равна , то интерференционные максимумы отраженных лучей и должны удовлетворять условию

. (4)

Таким образом, каждое семейство атомных плоскостей будет давать ряд отражений в зависимости от того, сколько значений может принимать величина m, чтобы оставался меньше единицы.

Соотношение (4), называемое уравнением Вульфа — Брэгга, является основным расчетным уравнением рентгеноструктурного и рентгеноспектрального анализа. При помощи этой формулы, если известны межплоскостные расстояния и измерить каким-либо образом углы скольжения, можно вычислить длины волн отраженных рентгеновских лучей. Зная длину волны монохроматических (характеристических) рентгеновских лучей и углы скольжения, можно определить межплоскостные расстояния.