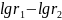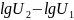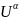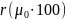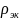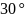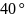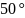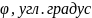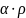- •Математическая основа карт
- •Содержание
- •Теория математической основы карт
- •Задание 1. Определение картографических проекций
- •Задание 2. Вычисление нормальной равноугольной конической проекции (с двумя главными параллелями)
- •Задание 3. Вычисление нормальной равноугольной цилиндрической проекции
- •Цилиндрической проекции с главными параллелями
- •Приложения
- •Список используемой литературы
Задание 2. Вычисление нормальной равноугольной конической проекции (с двумя главными параллелями)
Цель задания. Вычислить и построить нормальную равноугольную коническую проекцию для карты в масштабе 1:25 000 000 (варианты задания в приложении 2).
 Пример
выполнения задания.
Территория ограничена меридианами с
долготой
Пример
выполнения задания.
Территория ограничена меридианами с
долготой
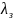 =40°
и
=40°
и
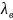 =80°
и параллелями с широтами
=80°
и параллелями с широтами
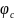 =
=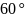 и
и
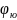 =
=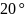 (рис. 6). Долгота среднего меридиана
(рис. 6). Долгота среднего меридиана
 =60°.
Картографическая сетка проведена через
10°, т. е. ∆
=∆
=60°.
Картографическая сетка проведена через
10°, т. е. ∆
=∆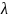 =10°
=10°
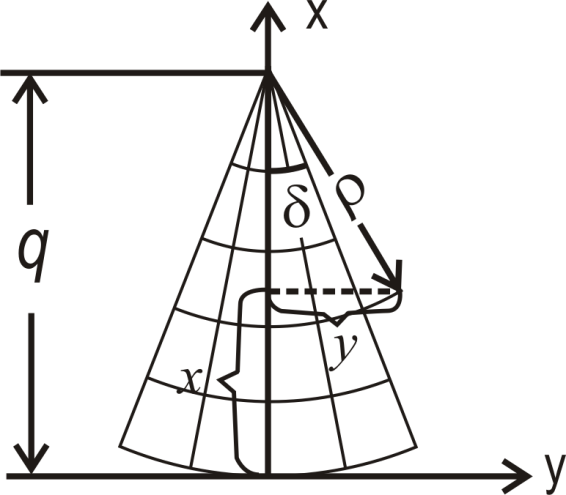
Рис 6. Сетка нормальной конической проекции Рис. 7. Сетка нормальной равноугольной конической проекции с двумя главными параллелями
Параметры
проекции
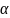 и
и
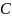 найти с условием, что на двух главных
параллелях с широтами
найти с условием, что на двух главных
параллелях с широтами
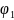 =30°
и
=30°
и
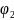 =50°
масштабы равны единице, т. е.
=50°
масштабы равны единице, т. е.
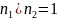
Параметры, используемые для вычисления:
- широта южной параллели территории;
- широта северной параллели территории;
- долгота западного меридиана территории;
- долгота восточного меридиана территории;
Δ - частота картографической сетки по широте;
Δ - частота картографической сетки по долготе;
Земная поверхность принимается за эллипсоид.
Формулы для вычисления проекции:
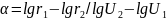 (1)
(1)
где r - радиусы параллелей земного эллипсоида;
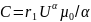 (2)
(2)
где α и - параметры проекции (постоянные величины);
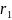 – радиус
главной параллели;
– радиус
главной параллели;
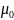 – масштаб
– масштаб
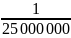 ;
;
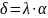 (3)
(3)
где
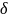 – полярный угол;
– полярный угол;
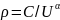 (4)
(4)
где
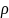 –
радиус параллелей в проекции;
–
радиус параллелей в проекции;
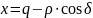 (5)
(5)
где
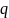 – расстояние между полюсом полярной
системы координат и началом счета
прямоугольных координат на проекции
(const
=
– расстояние между полюсом полярной
системы координат и началом счета
прямоугольных координат на проекции
(const
=
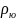 );
);
– экваториальный радиус;
– радиус параллелей на проекции;
– прямоугольная координата;
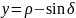 (6)
(6)
где – прямоугольная координата;
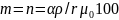 (7)
(7)
где
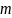 – масштаб по меридиану;
– масштаб по меридиану;
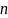 – масштаб
по параллели;
– масштаб
по параллели;
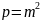 (8)
(8)
где p – масштаб площади;
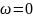
где
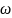 – максимальное искажение углов в
проекции;
– максимальное искажение углов в
проекции;
Значение
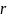 ,
,
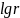 ,
,
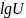 выбирают в зависимости от широты
параллелей из приложение 3.
выбирают в зависимости от широты
параллелей из приложение 3.
Вычисления параметров и высчитывают по формулам (1) и (2), записываются в табл. 8 и табл. 9
Таблица 8
Вычисление параметров
формула |
Вычисленные значения для широт |
|
|
|
|
|
6,7425955 6,6136233 0,2371064 0,4367044
0,1289722 0,1995980 0,6461597 |
|
Таблица 9
Вычисление параметров
Обозначение, формула |
Вычисление значения для широт |
|
φ1 |
φ1 |
|
|
0,2371064 0,4367044 0,6461597 |
|
lgU
|
0,1532086
1,4230121 22,113396 |
0,2821807
1,9150525 16,431732 |
=
|
48,6995 |
48,6995 |
Вычисление
полярного угла
.
Полярный угол
высчитывают по формуле (3), данные
приводят в табл. 10 по разностям долгот
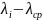 ,
где
,
где
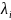 =70,
80,
=60.
=70,
80,
=60.
Таблица 10
Вычисление полярного угла δ
обозначение |
Вычисление значения по разностям долгот |
|
100 |
200 |
|
|
0,6461597 100 |
200 |
|
6,461612 |
12,9232 |
Вычисление радиуса параллелей. Радиус параллелей проекции высчитывают по формуле (4), данные приводят в табл. 11
Таблица 11
Радиусы параллелей проекции
Обозначение, формула |
Вычисленные значения для широт |
||||
|
|
|
|
|
|
|
0,6461597 0,1537787 |
0,2371064 |
0,3294572 |
0,4367044 |
0,5694259 |
, см , см |
0,0993655 |
0,1532086 |
0,2128819 |
0,2821807 |
0,3679400 |
1,257087 |
1,423012 |
1,632608 |
1,915052 |
2,333136 |
|
48,6995 |
|
|
|
|
|
38,7400 |
34,2228 |
29,8293 |
24,4299 |
20,8730 |
|
∆ , см |
4,5172 4,3935 4,3994 4,5569 |
||||
Вычисление прямоугольных координат и высчитывают по формулам (5) и (6), данные приводят в табл. 12; –const, близкое к значению радиуса южной параллели. В примере =40 см.
Таблица 12
Вычисление прямоугольных координат
|
Обозначение, формула |
Вычисленные значения для долгот |
||
=60 |
50 и 70 |
40 и 80 |
||
|
cos sin |
00 1.0 0 |
6.46160 0.99365 0.11254 |
12.92320 0.97465 0.22364 |
, см , см cos , см , см |
1,260 40,000 38,740 38,740 0,0 |
1,506 40,000 38,494
4,360 |
2,241 40,000 37,759
8,664 |
|
|
, см , см cos , см , см |
5,777 40,000 34,223 34,2228 0,0 |
5,995 40,000 34,005
3,851 |
6,644 40,000 33,356
7,654 |
|
, см , см cos , см , см |
10,171 40,000 29,829 29,8293 0,0 |
10,360 40,000 29,640
3,357 |
10,926 40,000 29,074
6,671 |
|
, см , см cos , см , см |
14,570 40,000 25,430 25,4299 0,0 |
14,732 40,000 25,268
2,862 |
15,214 40,000 24,786
5,687 |
|
, см , см cos , см , см |
19,127 40,000 20,873 20,8730 0,0 |
19,260 40,000 20,740
2,349 |
19,656 40,000 20,344
4,668 |
Таблица 13
Значения абсцисс и ординат
|
обозначение |
Прямоугольные координаты (в см) для меридианов с долготами |
||
λср = 600 |
500 и 700 |
400 и 800 |
||
|
|
1,260 0.0 |
1,506 4,360 |
2,241 8,664 |
|
|
5,777 0,0 |
5,995 3,851 |
6,644 7,654 |
|
|
10,171 0,0 |
10,360 3,357 |
10,926 6,671 |
|
|
14,570 0,0 |
14,732 2,862 |
15,214 5,687 |
|
|
19,127 0,0 |
19,260 2,349 |
19,656 4,668 |
На основании табл. 13 на миллиметровой бумаге строят сетку нормальной равноугольной конической проекции с двумя главными параллелями. Начинают строить с правой стороны, затем в зеркальном отражении переносят координаты точек на левую сторону. Меридианы - прямые линии, параллели – дуги концентрической окружности (рис. 7).
Вычисление
значения частных масштабов (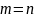 )
и масштаба площади р
высчитывают по формулам (7) и (8), данные
записывают в табл. 14.
)
и масштаба площади р
высчитывают по формулам (7) и (8), данные
записывают в табл. 14.
Таблица 14
Вычисление частных масштабов и масштаба площади
Обозначение, формула |
Вычисленные значения для широт φ |
||||
|
|
|
|
|
|
|
0,64616 25,032 23,984 1,044 1,090 |
22,114 22,114 1,000 1,000 |
19,274 19,571 0,985 0,970 |
16,432 16,432 1,000 1,000 |
13,4857 12,788 1,055 1,113 |
Н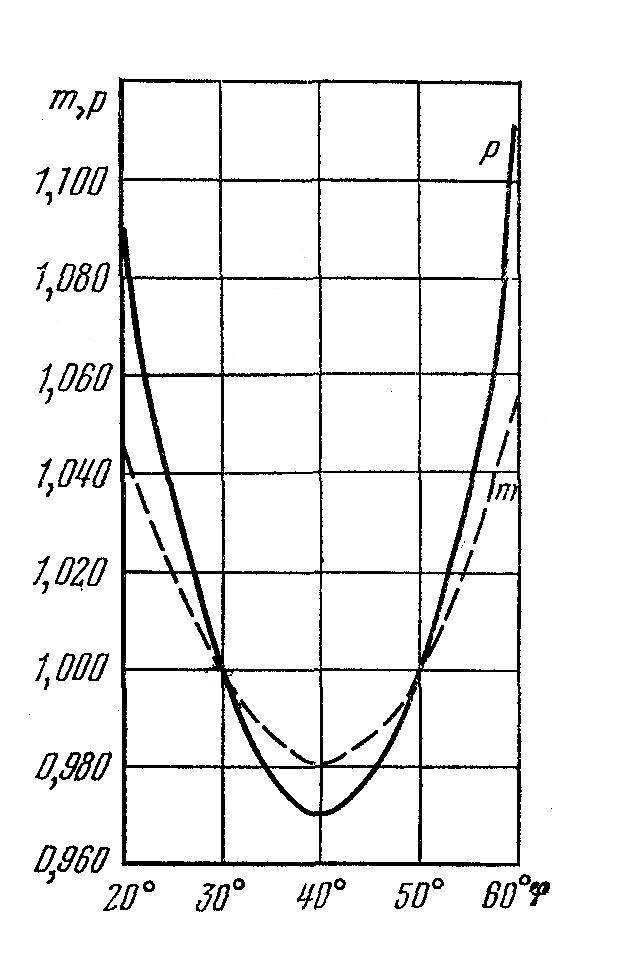 а
основании найденных масштабов длин и
площадей строят график масштабов m и p
(рис.8).
а
основании найденных масштабов длин и
площадей строят график масштабов m и p
(рис.8).
Рис. 8. График масштабов длин и площадей в нормальной равноугольной конической проекции