Завдання для практичної роботи

Розв'язати графічним методом ЗЛП:

Варіант 1 Варіант 2

Варіант 3 Варіант 4

Варіант 5 Варіант 6

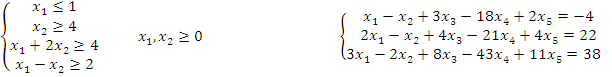
Варіант 7 Варіант 8

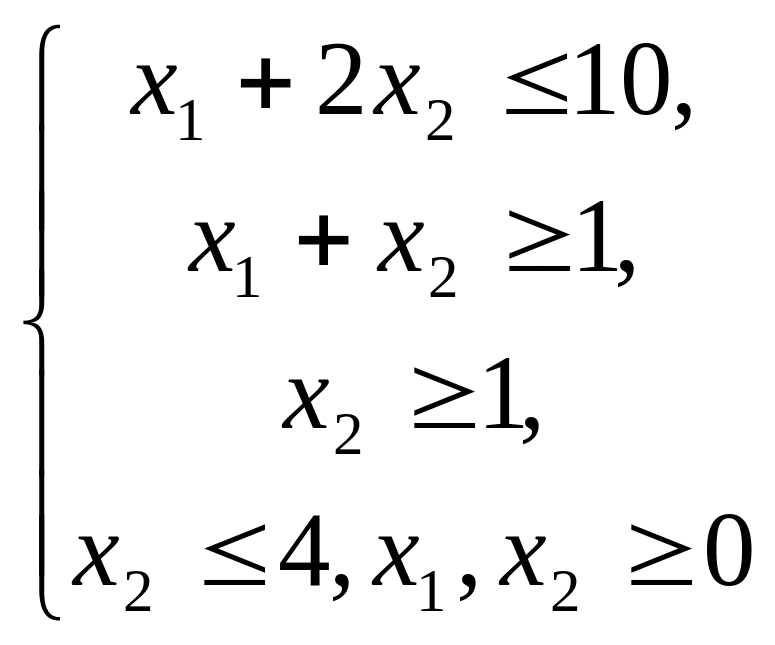
Приклад виконання практичної роботи.

Мета: закріпити та поглибити знання, отримані під час теоретичного заняття; навчитись застосовувати графічний метод до розв’язування практичних задач лінійного програмування; розвинути мислення та вміння аналізувати, робити висновки.

Обладнання: калькулятор, лінійка, олівець, ручка, методичні вказівки.

Хід роботи

1. Розв'язати графічно злп.

Знайти максимум функції Z=10x₁+15x₂ –> max

за умов

Розв'язання: Геометричну інтерпретацію задачі наведено на рис. 2.8.

Область допустимих розв'язків дістаємо так. Обмеження визначає півплощину з граничною прямою . Будуємо її і визначаємо півплощину, яка описується нерівністю .

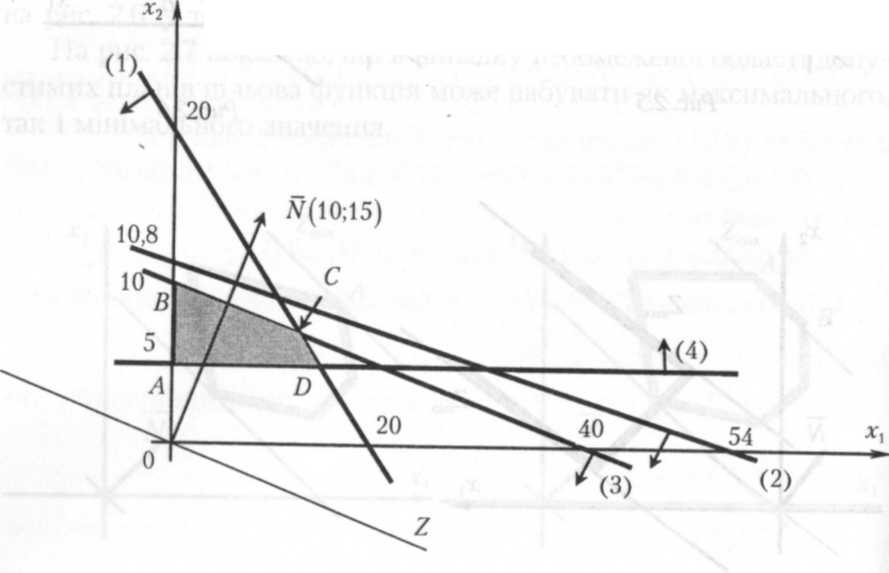Рис. 2.8

З цією метою в нерівність підставляє­мо координати якоїсь характерної точки, скажімо х₁ = х₂ = 0.Переконуємося, що ця точка належить півплощині . Цей факт на рис. 2.8 ілюструємо відповідною напрямленою стрілкою. Аналогічно будуємо півплощини, які відповідають решті нерівностей обмежень ЗЛП. У результаті перетину цих півплощин утворюється область допустимих розв'язків задачі (на рис. 2.8 — многокутник АВСD).

Вектор N(10:15) задає напрям зростання значень цільової функції Z.

Цільова функція Z=10x₁+15x₂ визначає сім'ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z=0, маємо 10x₁+15x₂=0. Ця пряма проходить через початок системи координат.

Переміщуючи пряму 10x₁+15x₂=0 в напрямі вектора N(10; 15), знаходимо крайню точку многокутника розв'язків. Нею є точка С — вершина многокутника розв'язків.

Знаходимо координати точки С, як точки перетину прямих х₁+х₂=20 i

2x₁ +8x₂=80.

Для цього розв'язуємо систему рівнянь

Її розв’язком є значення

Отже,і є розв’язком ЗЛП.

2. Розв'язати графічно ЗЛП. Знайти

за умов Розв'язання.

Застосовуючи метод Жордано-Гаусса здійснимо виключення з системи обмежень задачі базисних змінних. У результаті таких перетворень система обмежень набуде вигляду

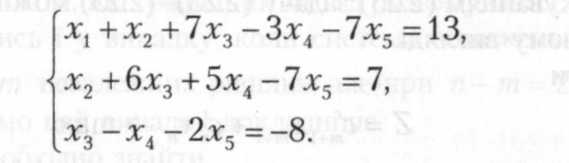
Звідси випливає:

Підставляючи значення базисних змінних у цільову функцію та вилучаючи їх з системи обмежень, початкову задачу можна представити в наступному вигляді.

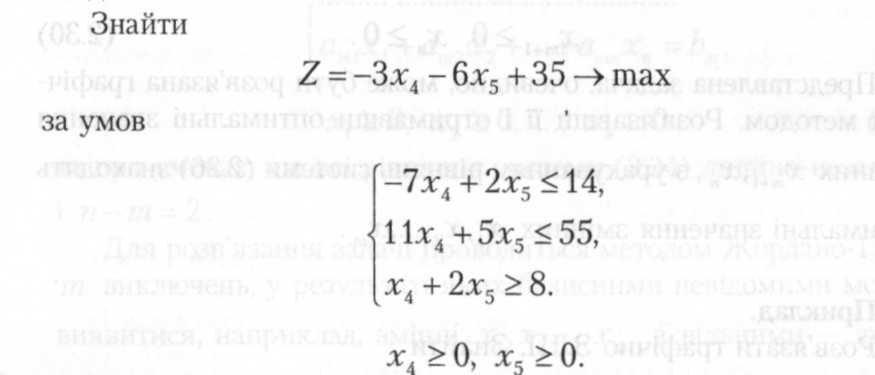
Остання може бути розв'язана графічним методом у системі координат Ox4x5. Многокутник розв'язків і графік лінійної функції, що визначається цільовою функцією, наведені на рис. 2.9.

З рис. 2.9 випливає, що максимального значення цільова фун­кція може набувати в точках A і D, а отже, і в будь-якій точці відрізка АD. Для перевірки цього та визначення оптимального плану необхідно, таким чином, знайти координати цих точок і оцінити значення цільової функції в них. Очевидно, що точка А має координати (0;4). Враховуючи, що точка D є точкою пере­тину прямих (2) і (3), для визначення її координат необхідно розв'язати систему рівнянь:

У результаті розв’язання останньої нескладно отримати, що

Оцінимо тепер значення цільової функції у точках A i D:

Таким чином функція Z набуває однакових значень в точках A i D. Це означає, що вона набуває того ж значення в усіх точках AD. Звідси тоді нескладно отримати, що опти­мальний розв'язок задачі, геометрична інтерпретація якої наведе­на на рис. 2.9, наступний: (-2С + 8;С), де

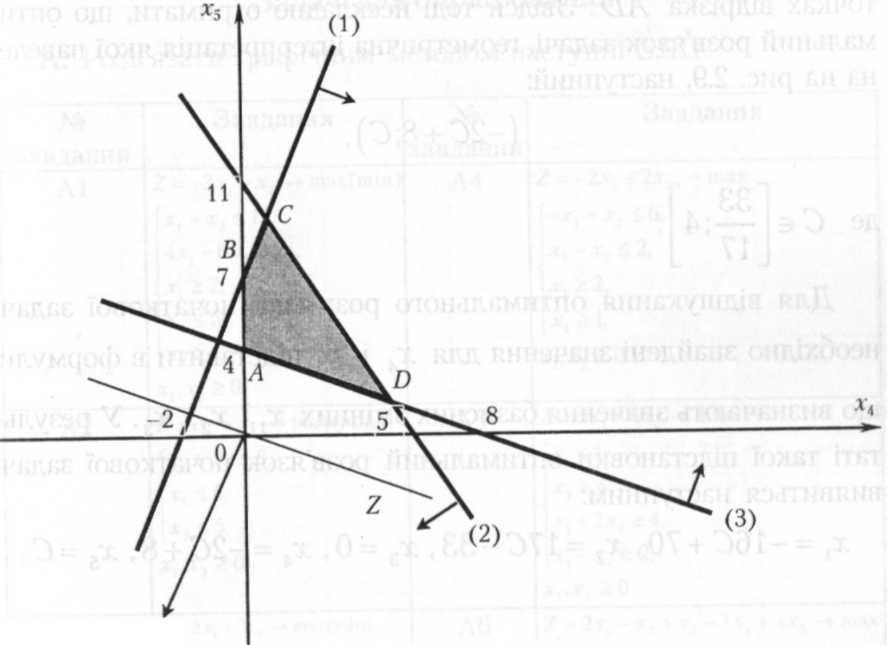рис. 2.9

Для відшукання оптимального розв'язку початкової задачі необхідно знайдені значення для х₄ і х₅ підставити в формули, що визначають значення базисних змінних х₁, х₂, х₃. У резуль­таті такої підстановки оптимальний розв'язок початкової задачі виявиться наступним:

х₁ = -16С + 70, х₂ = 17С-33, х₃ = 0, х_А = -2С + 8, х₅=С.

Висновок:

Отже, ми знайшли оптимальні розв᾽язки задач графічним методом, навчились застосовувати графічний метод до розв’язування практичних задач лінійного програмування.