Геометрична інтерпретація злп

Загальна задача лінійного програмування (1)—(3) геомет­рично інтерпретується так: кожне і -те обмеження, що має вигляд рівняння

у п -вимірному просторі основних змінних х_1,х₂,...,х_п задає гіперплощину. Кожному обмеженню виду (2) і (3) відповідають або гіперплощина, або гіперпівпростір, який лежить по один бік від відповідної гіперплощини. В результаті перетину всіх гіперпівпросторів, що визначаються обмеженнями задачі (2) і (3), утво­рюється опуклий многогранник її допустимих розв'язків. Цільову функцію в п -вимірному просторі основних змінних можна геометрично інтерпретувати як сім'ю паралельних гіперплощин, положення кожної з яких визначається значенням параметра Z. Отже, геометрична інтерпретація ЗЛП являє собою відшукан­ня такої точки многогранника розв'язків, в якій цільова лінійна функція набуває максимального (мінімального) значення.

Приклад.

У випадку розгляду ЗЛП в симетричній формі при п = 2 можна отримати, що системи обмежень (2)-(3) визначають перетин півплощин. Останній являє собою многокутник розв'язків ЗЛП. Він може бути точкою, відрізком, променем, многокутни­ком, необмеженою многокутною областю.

У випадку розгляду ЗЛП в симетричній формі при п = З можна отримати, що системи обмежень (2)-(3) визначають перетин півпросторів. Останній являє собою многогранник роз­в'язків ЗЛП. Він може бути точкою, відрізком, променем, много­кутником, многогранником, многогранною необмеженою областю.

3. Властивості розв'язків задачі лінійного програмування

Теорема.

Множина всіх планів ЗЛП опукла.

Теорема.

Цільова лінійна функція ЗЛП набуває свого максимального (мінімального) значення в кутовій точці многогранника розв'язків.

Якщо цільова лінійна функція ЗЛП набуває свого максималь­ного (мінімального) значення більш ніж в одній кутовій точці, то вона досягає того ж значення в довільній точці, що є опуклою лінійною комбінацією цих точок.

Теорема. Якщо X = (х₁,х₂,...,х_n )— кутова точка многогранника розв'язків, то вектори в розкладі (2), що відповідають додатнім х_j є лінійно незалежними.

З властивостей розв'язків ЗЛП, що представлені в вигляді теорем, випливає, що якщо цільова лінійна функція ЗЛП обмежена на многограннику розв'язків, то:

1) існує така кутова точка многогранника розв'язків, в якій цільова лінійна функція ЗЛП досягає свого оптимуму;

2) кожний опорний план відповідає кутовій точці многогранника розв'язків.

Отже, для розв'язання ЗЛП необхідно дослідити лише кутові точки многогранника розв'язків, тобто лише опорні плани.

4. Графічний метод розв'язування задачі лінійного програмування

Графічний метод розв'язування ЗЛП базується на її геометричній інтерпретації та аналітичних властивостях і застосовується, як правило, при розв'язуванні ЗЛП при n= 2 та в окремих випадках при n = 3, оскільки досить важко побудувати многогранник розв'язків, що утворюється в результаті перетину півпросторів.

ЗЛП при п > 3 зобразити геометрично взагалі неможливо.

Розглянемо ЗЛП принципи п = 2 і розв'яжемо її графічним методом.

Знайти екстремум (максимум, мінімум) функції:

(1.2)

(2.2) (3.2)

Припустимо, що система (2.2) сумісна й мно­гокутник її розв'язків обмежений.

Згідно з геометричною інтерпретацією ЗЛП кожне і-те обмеження-нерівність (2.2) визначає півплощину з граничною прямою

(і = 1,…,т). Системою обмежень (2.2) описується спільна частина, або переріз усіх зазначених півплощин, тобто множина точок, координати яких задовольняють всі обмеження (2.2).

Цільова функція ЗЛП геометрично інтерпретується як сім'я паралельних прямих c₁x₁ +с₂х₂ = const.

З урахуванням властивостей розв'язків ЗЛП розв'язати ЗЛП графічно означає знайти таку вершину многокутника розв'язків, у результаті підставляння координат якої в (1.2) лінійна цільова функція набуде найбільшого (найменшого) значення.

Алгоритм графічного методу розв'язування ЗЛП

1. Будуємо прямі лінії, рівняння яких дістаємо заміною в об­меженнях (2.2) знаків нерівностей на знаки рівностей.

2. Визначаємо півплощини, що відповідають кожному обме­женню задачі.

3. Знаходимо многокутник розв'язків ЗЛП.

4. Будуємо вектор N = (c₁; с₂), що задає напрям зростання зна­чень цільової функції задачі.

5. Будуємо пряму с₁х₁+с₂х₂ = const, перпендикулярну до вектора N = (c₁;c₂).

6. Переміщуючи пряму с₁х₁+с₂х₂ = const в напрямі вектора N = (с₁;с₂) (для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину многокутника роз­в'язків (останню спільну точку графіка цільової функції і ОДР), де цільова функція досягає екстремального значення.

7. Визначаємо координати точки, в якій цільова функція на­буває максимального (мінімального) значення, і обчислюємо ек­стремальне значення цільової функції в цій точці.

При застосуванні графічного методу для розв'язування ЗЛП можливі такі випадки:

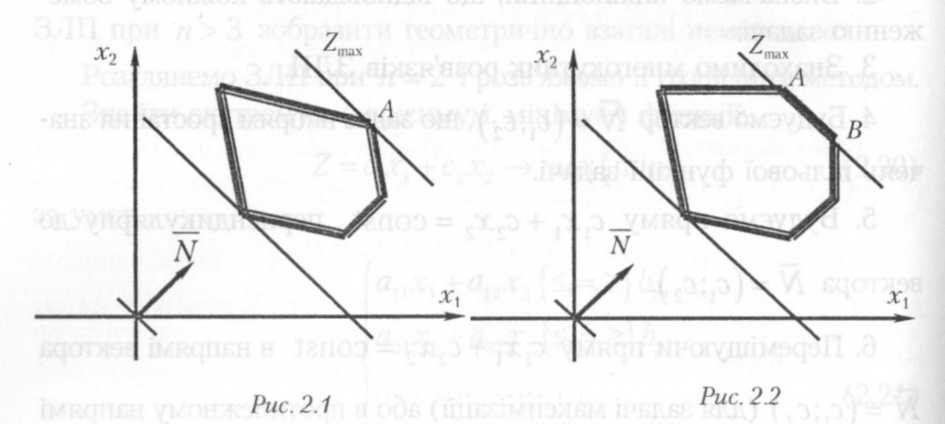
Цільова функція набуває максимального значення в єдиній

вершині А многокутника розв'язків (рис. 2.1).

Максимального значення цільова функція досягає в будь-якій

точці відрізка АВ (рис. 2.2). Тоді ЗЛП має альтернативні опти­мальні плани.

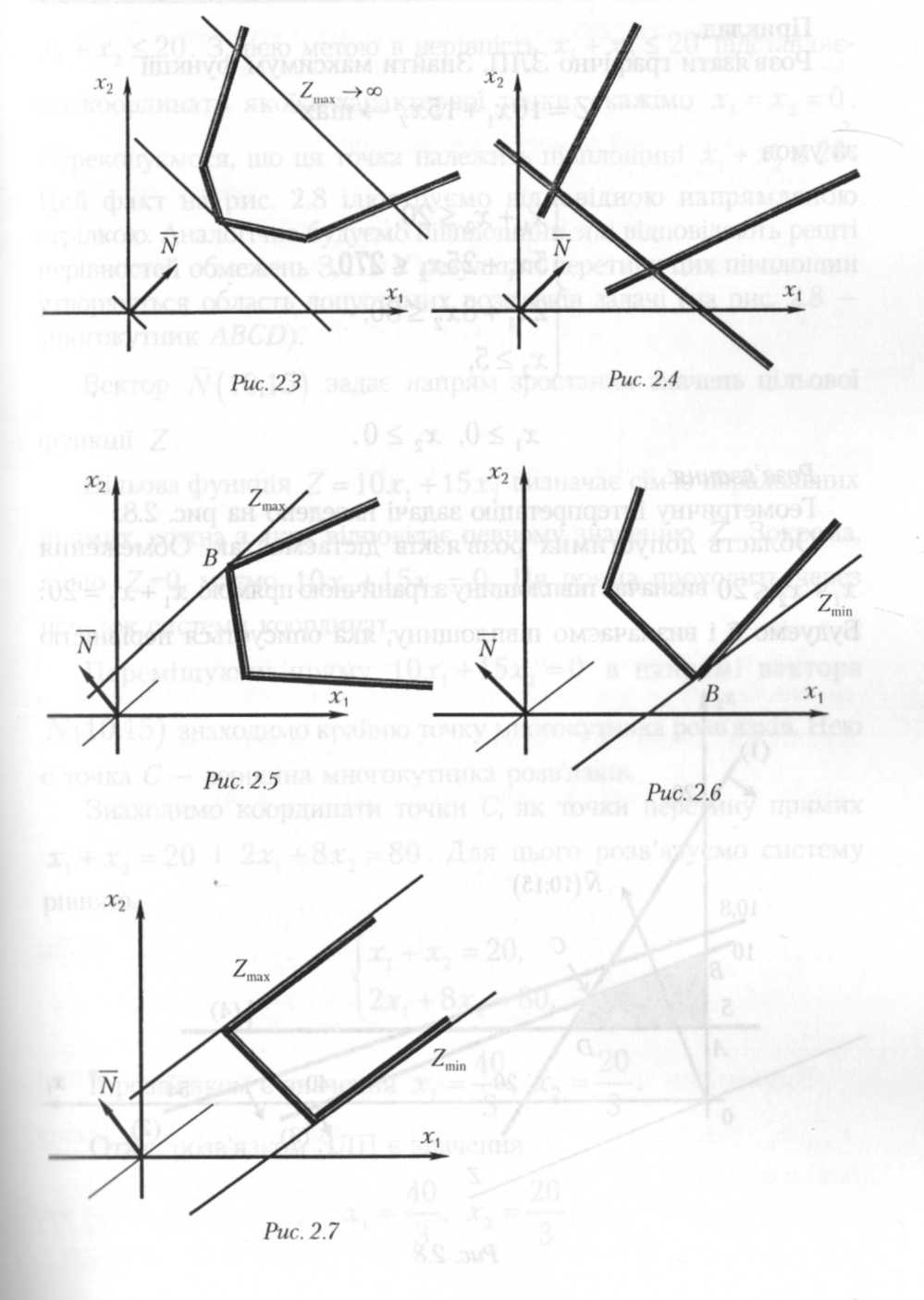
ЗЛП не має оптимальних планів (рис. 2.3 — значення цільової функції рівне нескінченності; рис. 2.4 — система обмежень задачі несумісна).

ЗЛП має оптимальний план за необмеженої області допусти­мих розв'язків (рис. 2.5, 2.6). На рис. 2.5 у точці В — максимум, на рис. 2.6. у точці В — мінімум.

На рис. 2.7 показано, що в випадку необмеженої області допу­стимих планів цільова функція може набувати як максимального, так і мінімального значень.