Завдання для практичної роботи

Розв᾽язати задачу методом потенціалів. Початковий опорний план

скласти методом подвійної переваги.

склади	області					запаси
	8		10	15	7	70
		11	12	9
	13		14	12	9
	7	15			10	60
потреби		30

У таблиці в залежності від варіанту може змінюватись у межах від 1 до 10, наприклад, для 5 варіанту .

Приклад виконання практичної роботи.

Мета: закріпити та поглибити знання, отримані під час теоретичного заняття; навчитись застосовувати розв’язування транспортних задач лінійного програмування для визначення найекономічнішого плану перевезення однорідної продукції від постачальників до споживачів; розвинути мислення та вміння аналізувати, робити висновки.

Обладнання: калькулятор, лінійка, олівець, ручка, методичні вказівки.

Хід роботи

Розв᾽язати методом потенціалів транспортну задачу, умова якої задана наступною таблицею:

Пункт	Споживач				Запас
	6	7	3	5	100
	1	2	5	6	150
	3	10	20	1	50
потреби	75	80	60	85	300

Розв’язання:

Початковий опорний план ТЗ:

Пункт	Споживач				Запас
	75 6	25 7	3	5	100
	1	55 2	60 5	35 6	150
	3	10	20	50 1	50
потреби	75	80	60	85	300

Для визначення потенціалів сформуємо систему лінійних рівнянь:

Поклавши в останній , відшукаємо потенціали початкового опорного плану ТЗ. Вони рівні:

Перепишемо останню таблицю, доповнивши її відповідними потенціалами .

Пункт	Споживач				Запас
	6 75	7 25	3	5	100
	1	2 55	5 60	6 35	150
	3	10	20	1 50	50
потреби	75	80	60	85	300

Перевіримо тепер виконання умови оптимальності для незаповнених клітин таблиці:

З наведених нерівностей випливає, що умова оптимальності не виконується для клітин (1.3) і (1.4). Тому необхідно перейти до нового опорного плану. Для цього слід вибрати клітинку, для якої необхідно здійснити цикл перерахування. Для вибору такої клітинки обчислимо

.

Отже, цикл перерахування слід здійснити для клітинки (1.3). Наступна таблиця перерозподілу продукції:

Пункт	Споживач				Запас
	6 75	- 7 2 5	+ 3	5	100
	1	+ 2 5 5	- 5 60	6 35	150
	3	10	20	1 50	50
потреби	75	80	60	85	300

При цьому в клітинки (1.3) і (2.2) переноситься 25 одиниць продукції, а з клітинок (1.2) і (2.3) така ж кількість продукції вилучається. З урахуванням цього новий опорний план ТЗ матиме вигляд, що наведений в наступній симплексній таблиці.

Пункт	Споживач				Запас
	6 75	7	3 25	5	100
	1	2 80	5 35	6 35	150
	3	10	20	1 50	50
потреби	75	80	60	85	300

Значення потенціалів випливає із системи, якщо покласти :

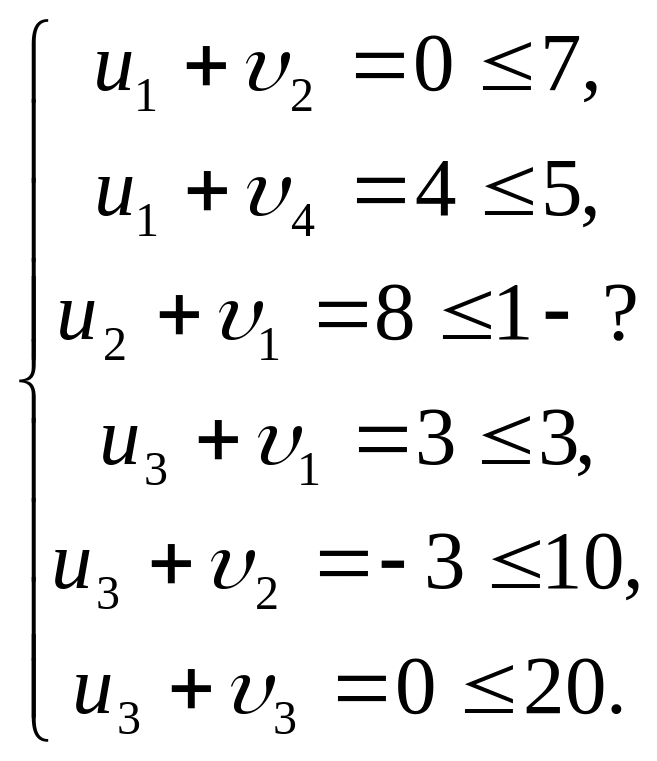
Пункт	Споживач				Запас
	- 6 75	7	+ 3 25	5	100
	+ 1	2 80	- 5 35	6 35	150
	3	10	20	1 50	50
потреби	75	80	60	85	300

При цьому в клітинки (1.3) і (2.1) переноситься 35 одиниць продукції, а з клітинок (1.1) і (2.3) така ж кількість продукції вилучається. З урахуванням цього новий опорний план ТЗ матиме вигляд, що наведений в наступній симплексній таблиці.

Пункт	Споживач				Запас
	6 40	7	3 60	5	100
	1 35	2 80	5	6 35	150
	3	10	20	1 50	50
потреби	75	80	60	85	300

Значення потенціалів випливає із системи, якщо покласти :

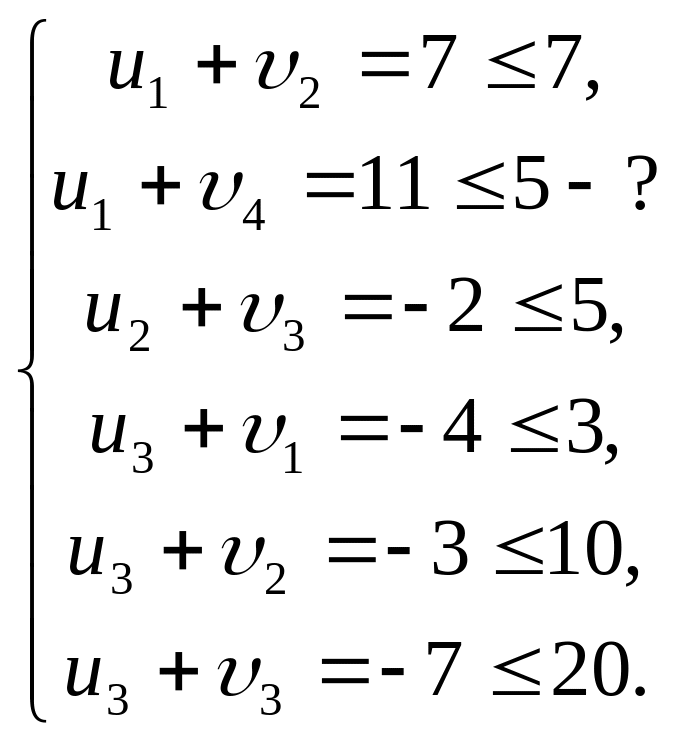
Отже, цикл перерахування слід здійснити для клітинки (1.4). Наступна таблиця перерозподілу продукції:

Пункт	Споживач				Запас
	- 6 40	7	3 60	+ 5	100
	+ 1 35	2 80	5	- 6 35	150
	3	10	20	1 50	50
потреби	75	80	60	85	300

При цьому в клітинки (1.4) і (2.1) переноситься 35 одиниць продукції, а з клітинок (1.1) і (2.4) така ж кількість продукції вилучається. З урахуванням цього новий опорний план ТЗ матиме вигляд:

Пункт	Споживач				Запас
	6 5	7	3 60	5 35	100
	1 70	2 80	5	6	150
	3	10	20	1 50	50
потреби	75	80	60	85	300

Значення потенціалів випливає із системи, якщо покласти :

З наведених нерівностей випливає, що умова оптимальності виконується для всіх перевірених клітин. А, отже, опорний план, що представлений в останній таблиці, є оптимальним.

Таким чином,

При цьому

Висновок: Отже, ми знайшли оптимальний розв᾽язок задачі, навчились розв᾽язувати транспортні задачі лінійного програмування.