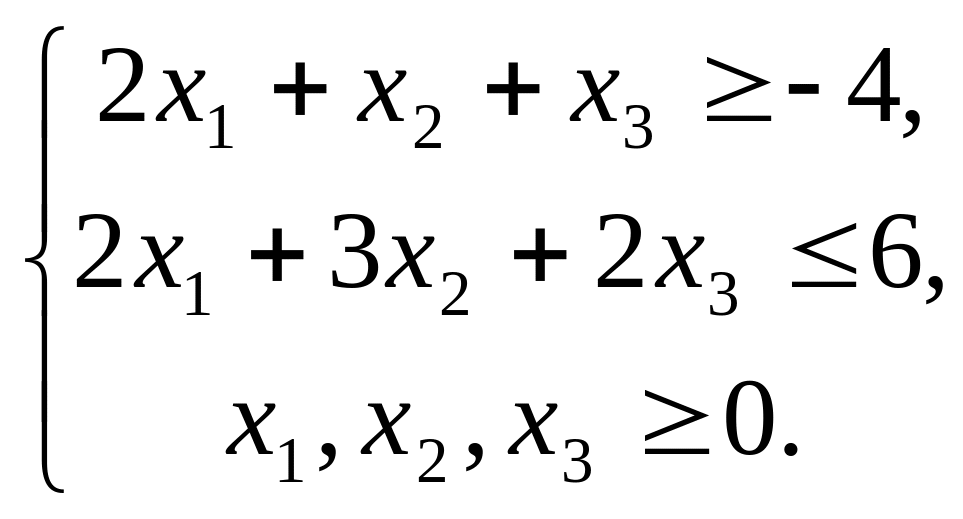- •«Графічний метод розв᾽язування задач лінійного програмування»
- •Теоретичні відомості
- •1. Постановка загальної задачі лінійного програмування
- •2. Геометрична інтерпретація задачі лінійного програмування
- •Геометрична інтерпретація злп
- •3. Властивості розв'язків задачі лінійного програмування
- •4. Графічний метод розв'язування задачі лінійного програмування
- •Завдання для практичної роботи
- •Приклад виконання практичної роботи.
- •Хід роботи
- •1. Розв'язати графічно злп.
- •Література:
- •Інструкція до проведення практичної роботи.
- •«Математичні методи дослідження операцій»
- •Анотація
- •«Симплексний метод розв᾽язування задач лінійного програмування»
- •Теоретичні відомості Симплекс-метод розв'язування злп.
- •Звести систему обмежень до канонічної форми:
- •2. Визначити початковий опорний план злп.
- •3. Побудувати симплексну таблицю.
- •Правило уникнення зациклювання призастосуванні симплекс-методу.
- •Завдання для практичної роботи
- •Хід роботи
- •Література:
- •Інструкція до проведення практичної роботи.
- •«Метод штучного базису розв᾽язування задач лінійного програмування»
- •Тема: Метод штучного базису розв᾽язування задач лінійного програмування
- •Теоретичні відомості Метод штучного базису розв'язування злп.
- •Завдання для практичної роботи
- •Хід роботи
- •Література:
- •Інструкція до проведення практичної роботи.
- •«Правила побудови двоїстих задач до задач лінійного програмування»
- •Тема: Правила побудови двоїстих задач до задач лінійного програмування.
- •Теоретичні відомості Правила побудови двоїстих задач до задач лінійного програмування.
- •Завдання для практичної роботи
- •Хід роботи
- •Література:
- •Інструкція до проведення практичної роботи.
- •«Математичні методи розв´язування транспортної задачі»
- •Тема: Математичні методи розв´язування транспортної задачі.
- •Теоретичні відомості Математичні методи розв´язування транспортної задачі.
- •Завдання для практичної роботи
- •Хід роботи
- •Література:
- •Інструкція до проведення практичної роботи.
Завдання для практичної роботи
Скласти двоїсту задачу до наступної ЗЛП. Розв᾽язати одну з них і знайти оптимальний план іншої ЗЛП.
№ варіанта |
завдання |
№ варіанта |
завдання |
1.
|
|
6. |
|
2. |
|
7. |
|
3. |
|
8. |
|
4. |
|
9. |
|
5. |
|
10. |
|
Приклад виконання практичної роботи.
Мета: закріпити та поглибити знання, отримані під час теоретичного заняття; навчитись застосовувати побудову двоїстих задач до розв’язування практичних задач лінійного програмування; розвинути мислення та вміння аналізувати, робити висновки.
Обладнання: калькулятор, лінійка, олівець, ручка, методичні вказівки.
Хід роботи
 Скласти
двоїсту задачу до наступної ЗЛП. Знайти
оптимальний план двоїстої, попередньо
розв᾽язавши пряму ЗЛП.
Скласти
двоїсту задачу до наступної ЗЛП. Знайти
оптимальний план двоїстої, попередньо
розв᾽язавши пряму ЗЛП.
![]()

Розв’язання:
Канонічна
форма:

Тоді
двоїста задача матиме вигляд:
![]()

Остання симплекс-таблиця прямої ЗЛП має такий вигляд:
i |
Базис |
С базиса |
А0 |
1 |
-1 |
-3 |
0 |
0 |
0 |
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
||||
1 2 3 |
А3 А2 А1 |
-3 -1 1 |
4 11/3 1/3 |
0 0 1 |
0 1 0 |
1 0 0 |
2 -1/3 -2/3 |
1 1/3 -1/3 |
0 2/3 1/3 |
m+1 |
Zj-Cj |
- |
0 |
0 |
0 |
-19/3 |
-11/3 |
-1/3 |
|
) є оптимальним і йому відповідає .
Отже,
залишається лише відшукати оптимальний
план двоїстої задачі. З урахуванням
того,що
![]() (див. стовпець
наведеної
симплекс-таблиці),
а
(див. стовпець
наведеної
симплекс-таблиці),
а
 (див. стовпці
(див. стовпці
![]() наведеної
симплекс-таблиці),
оптимальний
план двоїстої задачі набуде вигляду:
наведеної
симплекс-таблиці),
оптимальний
план двоїстої задачі набуде вигляду:

При
цьому
![]()
 Очевидно,
що
Очевидно,
що
![]() .
.
Висновок: Отже, ми знайшли оптимальний розв᾽язок задачі, навчились будувати двоїсті задачі лінійного програмування.
Література:
1. Барвінський А.Ф. Математичне програмування: Навчальний посібник. Львів: Національний університет «Львівська політехніка», 2004.- 448с.
2. Боровик О.Л., Боровик Л.В. Дослідження операцій в економіці: Навчальний посібник. Київ: Центр учбової літератури, 2007. - 422 с.
3. Бугір М.К., Якімов Ф.П. Посібник по розв᾽язуванню задач з математичного програмування: Навчальний посібник. – Тернопіль, 1997. – 430 с.
4. Вітлінський В.В., Наконечний С.І., Терещенко Т.О. Математичне програмування. – Київ: КНЕУ, 2001. - 248 с.
5. Ульянченко О.В. Дослідження операцій: підручник для студентів вузів. Харк. нац. аграр. Ун-т ім.В.В. Докучаєва. – харків: Гриф, 2002. – 580 с.
6. Цегелик Г.Г. Лінійне програмування. – Львів: Світ, 1995. – 216 с.
Зміст звіту.
1. Титульний аркуш.
2. Тема, мета виконання практичної роботи, обладнання.
3. Хід роботи: короткі теоретичні відомості, основні формули; виконання практичного завдання з посиланням на твердження та формули.
4. Висновок.
5. Література.