Чтение и запись данных

В пакете Maxima имеются стандартные функции для чтения данных из файла, а также записи или добавления данных в файл.

Чтение данных производится с помощью функций

data : read_list("Путь к файлу");

data : read_nested_list("Путь к файлу");

Функция read_list( ) считвает из файла значения, расположенные в одной строке, разделённые пробелом, и помещает их в список data. Функция read_nested_list( ) расценивает содержимое файла как список строк. Каждая строка может содержать несколько данных, разделённых пробелом, которые тоже являются списком. Поэтому переменная data представляет собой список списков, например

(%i1) data : read_nested_list("d:/5555.dat");

(%o1) [[1,1],[2,5],[3,8],[4,3],[5,12],[6,20],[7,9],[8,8],[9,7],[10,5]]

При этом размер списков устанавливается в соответствии с объемом файла. Данные первого столбца файла можно извлечь из перемненной data с помощью команды

(%i2) k : makelist(first(data[i]),i,1,length(data));

(%o2) [1,2,3,4,5,6,7,8,9,10].

Аналогично для второго стобца

(%i3) kw:makelist(second(data[i]),i,1,length(data));

(%o3) [1,5,8,3,12,20,9,8,7,5]

и т.д.

Перед считыванием файл можно найти с помощью команды

file_search("Путь к файлу");

а также вывести на экран

printfile("Путь к файлу");

Для записи данных в файл следует воспользоваться функцией

write_data(Список,"Путь к файлу");

Список выводится в строку. Значения разделяются пробелом.

Для добавления данных к существующему файлу необходимо изменить значение переменной

file_output_append : true;

и использовать для вывода функцию write_data( ).

Чтобы записать в файл значения элементов списка в столбец, можно воспользоваться следующей последовательностью команд

file_output_append:true;

for m:1 thru length(x) do write_data([y[m]],"Путь к файлу");

Здесь с помощью цикла по очереди выводятся в файл значения элементов списка.

Часть III. Лабораторные работы лабораторная работа № 1 функциональный масштаб. Интерполяция

ОБЩИЕ СООТНОШЕНИЯ. Для удобного графического представления функциональной зависимости y=f(х) могут применяться: a) логарифмический масштаб; b) обратный функциональный масштаб; c)прямой функциональный масштаб.

ОБРАТНЫЙ ФУНКЦИОНАЛЬНЫЙ МАСШТАБ . Пусть y=f(х)=f(kx). Преобразуем график в прямую линию у*=kx. Это можно сделать преобразованием . Если исходная функция имеет более общую зависимость , то данное преобразование координаты у дает уравнение в системе координат (x,y*)

Пример: у = 1-ехр(- k(x-с)), х > с. Преобразование у* = —ln(1-у) приводит к уравнению прямой линии у* = k(x-c).

Обратный функциональный масштаб удобно применять к "S" -образным кривым.

ПРЯМОЙ ФУНКЦИОНАЛЬНЫЙ МАСШТАБ . Пусть y=f(x)=kf₁(x)+c. Тогда преобразование х* = f₁(x) приводит график к прямой линии у = kx* + с. Такой функциональный масштаб целесообразно использовать для "U" и "J"-образных кривых.

Пример: . Тогда у = 5х* -2.5. Обратите внимание, что обратный функциональный масштаб в этом примере менее удобен, так как бесконечную кривую он преобразует в конечный отрезок прямой , а это приведет к сгущению точек на концах отрезка.

ВЕРОЯТНОСТНАЯ БУМАГА. Вероятностной бумагой называется функциональный масштаб, в котором функция распределения F(x) случайной величины х преобразуется в прямую линию. Для этого случая необходимо применить обратное функциональное преобразование у* = F^-1 (y) . Если на вероятностной бумаге построить полигон накопленных частот Р_q (х_q ), х_q[a;a+q], где , то:

1. нелинейная зависимость 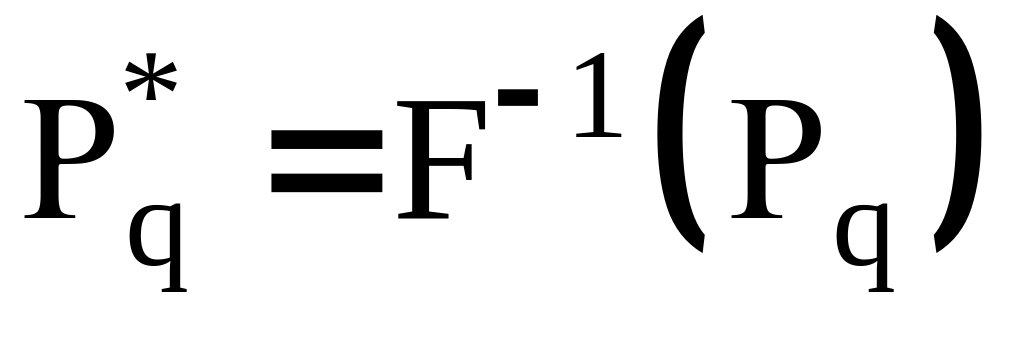от х_q указывает на несоответствие эмпирической и теоретической функций распределения; линейная зависимость, напротив, говорит о соответствии эмпирической и теоретической функций распределения;

2. по линейной зависимости легко найти параметры с и s в функции распределения F(x) случайной величины х.

,