Списки.

В программе Maxima существует понятие списка. Это упорядоченная совокупность объектов (могут быть разных типов: выражения, формулы, числа, списки...). Для задания списка объекты перечисляются через запятую в квадратных скобках, например: sp1:[a,b,c,45,k+m]. Пустые квадратные скобки означают пустой список. Создать список позволяет функция makelist:

makelist(Выражение, переменная, начальное значения, конечное значение),

например,

lst:makelist(i^2,i,1,10)

[1,4,9,16,25,36,49,64,81,100]

получаем список квадратов целых чисел от 1 до 10. Аналогом команды makelist является пункт меню «Алгебра -> Создать список (Make List)».

Массивы.

Массив в Maxima — это совокупность объектов с индексами (похож на индексированный список). Существуют несколько способов работы с массивами. Значения элементов массива произвольного размера задаются или «индивидуально»:

mas[1]:20$

mas[5]:45$

или как функция индексов

mas[i,j]:=i^2+j^2

Массив определенного размера можно определить командой

array(ИмяМассива,Тип,Размер1,Размер2,...).

Здесь Тип — тип элементов массива (float — вещественный, int — целый). Индексы массива принимают значения от 0 до указанного размера.

Например, команда

array(mas,float,5,5)

определяет двумерный массив 6 на 6 с именем mas, состоящий из вещественных элементов. Если тип элементов массива неизвестен его можно не указывать.

Векторы и матрицы.

В Maxima можно использовать прямоугольные матрицы. Для удобства команды работы с матрицами представлены также в меню «Алгебра».

Для создания матрицы служит функция matrix:

matr1:matrix([1,2,3],[4,6,8],[-1,2,4])

или пункт меню «Ввести матрицу».

Доступ к элементам матрицы осуществляется по двум индексам mart[2,1]. Первый индекс означает номер строки, второй — номер столбца. Нумерация начинается с 1.

Функция

genmatrix(ИмяМассива, Разм1, Разм2)

генерирует матрицу на основе двумерного массива. Ей соответствует пункт меню «Создать матрицу».

Функция

zeromatrix(N,M)

возвращает матрицу размерности MxN, состоящую из нулей.

Функция

ident(N)

возвращает единичную матрицу размерности NxN.

Функция

Матрица1:copymatrix(Матрица2)

создаёт копию матрицы.

Maxima позволяет выполнить все допустимые операции с матрицами. Возвести каждый элемент матрицы в степень можно с помощью операции ^. Для возведения матрицы в степень по правилам линейной алгебры используется двойная крышка ^^.

Например, обратную матрицу получаем, указав (–1) степень (или в меню «Обратить матрицу»), а для операции транспонирования используем функцию transpose (или меню «Транспонировать матрицу»). Функция determinant и пункт меню «Определитель» вычисляют определитель. В следующем примере получаем решения квадратного уравнения для нескольких исходных данных:

(%i2) a:matrix([5,3,8]);

(%o2) [5 3 8]

(%i3) b:matrix([3,2,1]);

(%o3) [3 2 1]

(%i4) c:matrix([6,4,0]);

(%o4) [6 4 0]

(%i5) (-b+sqrt(b^2-4*a*c))/(2*a);

(%o6)

(%i6) (-b+sqrt(b^2+4*a*c))/(2*a);

(%o6)

Построение графиков функций.

Функции в Maxima употребляются в двух смыслах: в математическом и «программистском». Для определения функции в математическом смысле достаточно написать, например, y:x^2+2. Maxima понимает, что переменная y есть функция переменной x. Для построения ее графика можно использовать функцию plot2d:

plot2d(y,[x,-5,5]).

Здесь первый аргумент y — функция, график которой строим, второй аргумент — список из трёх элементов: х — переменная, -5 и 5 — границы отрезка построения по оси абсцисс. При необходимости построить несколько графиков вместо первого аргумента функции plot2d нужно указать список функций, например

plot2d([y,z],[x,-5,5]).

Если функция имеет параметр, например, , где a — параметр, то её нужно определять как функцию в программистском смысле, зависящую от основного аргумента х и от параметра а:

y(a,x):=a*x^2.

Здесь для присваивания использован оператор «:=».

При построении нужно указывать конкретные значения параметра, например

plot2d([y(2,x),y(4,x)],[x,-5,5]).

График функции можно строить также по точкам, то есть по заранее вычисленным значениям переменных х и у. Для этого необходимо задать интервал изменения аргумента в виде списка:

x:makelist(k*0.2, k, 0, 100);

Затем нужно определить функцию в «программистском» смысле

f(x):=x*sin(x);

вычислить значения функции для каждого элемента списка, например, так

y:map(f,x),numer;

и построить график по точкам

plot2d([discrete,x,y]);

В результате получим график, изображенный на рис. 3.

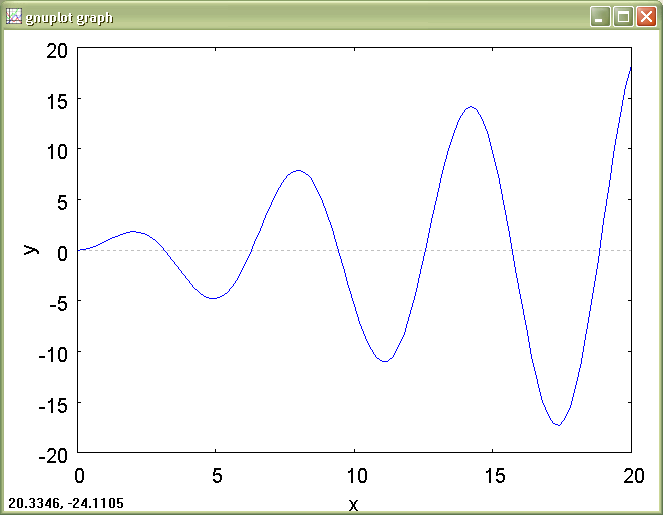
Рис. 3 Пример графика функции

Построение графиков двух переменных рассмотрим на простом примере. Определим фунуцию двух переменных

ff(x,y):=exp((-x^2-y^2)/20);

строим 3d график

plot3d(ff(x,y),[x,-5,5],[y,-5,5]);

получаем график, изображённый на рис. 4

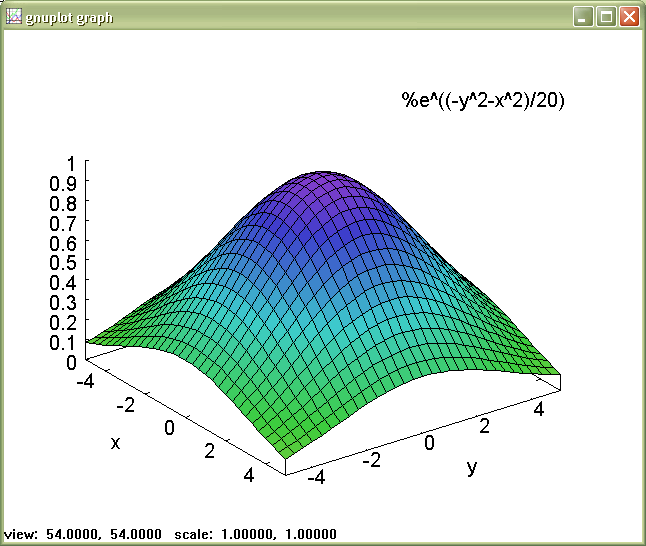
Рис. 3 Трехмерный график