Задание “а” (Моделирование выборки)

1. Обратиться к датчику-генератору случайных величин из библиотеки стандартных функций Matcad или МAXIMA

   1. rnorm(n,,), random_normal(m,s,n);

   2. rexp(n,), random_exp(,m);

   3. rchisq(N, nn), random_chi2(n,m);

   4. rpois(n, ), random_poisson (,n);

5. rbinom(n,k,p), random_binomial(k,p,m);

6. rgamma(n,c), random_gamma(с,1,n);

7. runif(n,a,b);

8. =1, 0.5,2. –датчик релеевской случайной величины.

2. Сформировать выборку объемом п = 10³ . Параметры процедуры задаются пользователем.

3. Вычислить выборочные моменты:

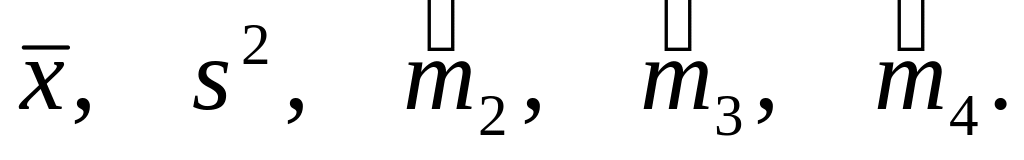
4. Определить выборочные коэффициенты асимметрии и эксцесса .

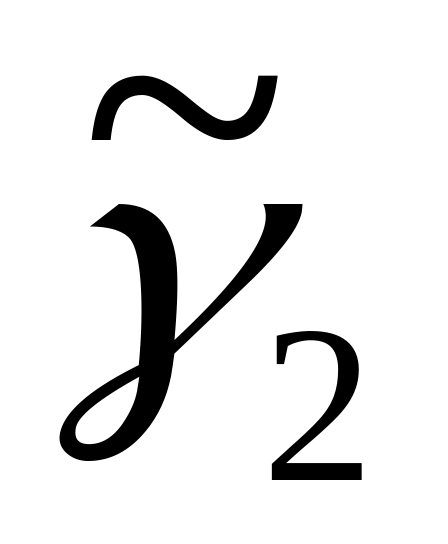5. Вычислить теоретические моменты распределений и сравнить с экспериментальными.

6. Определить доверительные границы оценок параметров для значений доверительных вероятностей Р₀ =0.9; 0.95;

Задание “в” (Выборка из файлов данных)

1. Считать данные из файлов V1.prn ….V12.prn

2. Определить тип случайной величины

3. Вычислить моменты

4. Определить выборочные коэффициенты асимметрии и эксцесса .

2. Выборочные распределения

ОБЩИЕ СООТНОШЕНИЯ. Теоретическими вероятностными характеристиками для непрерывной случайной величины являются: плот- ность вероятности ; функция распределения .

Для дискретной случайной величины :

распределение вероятностей функция распределения

При проведении эксперимента теоретическое распределение F_(x) может быть:

1. либо известно частично, с точностью до некоторых неизвестных параметров;

2. либо полностью неизвестным.

В первом случае экспериментальное определение сводится к оценке параметров распределения, которые находятся из выборочных моментов , рассмотренных в части I работы.

Во втором случае производится непараметрическая оценка распределения на основе 1) эмпирической функции распределения, 2) гистограммы, 3) полигона накопленных частот. Эмпирической функции распределения называется оценка F_(x) по несгруппированной выборке. Гистограммой называется оценка плотности вероятности по сгруппированным данным. Полигоном накопленных частот называется оценка функции распределения по сгруппированным данным.

I.Правило построения эмпирической функции распределения.

1. Берется выборка 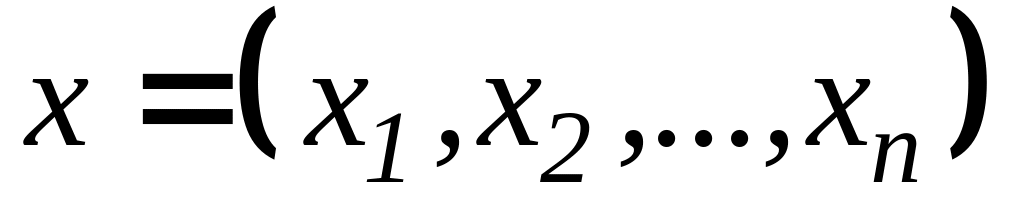объемом n>100, производится ее упорядочивание .

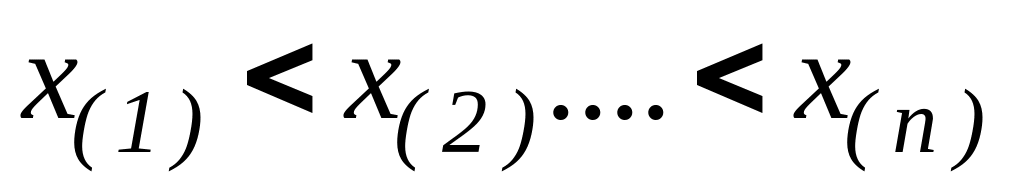2. Строится функция 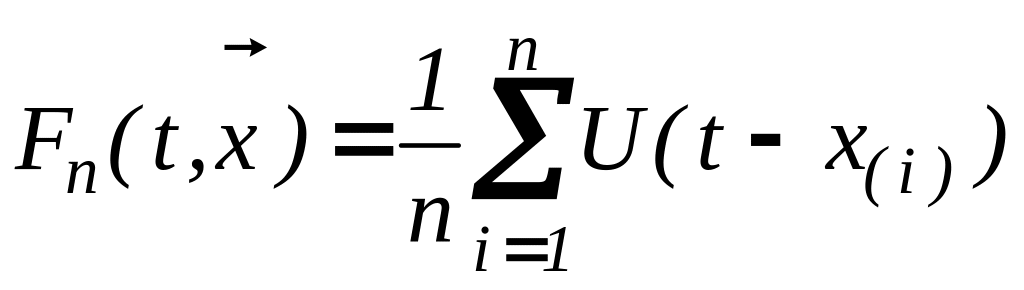, где U(t)- функция Хевисайда

II. Правило построения гистограмм:

1. Берется выборка 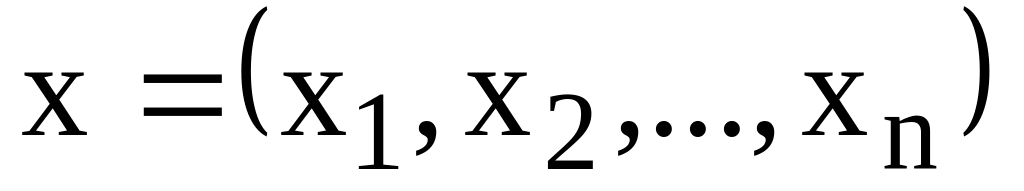объемом n>100, как правило, .

2. Определяется число интервалов группировки r:

a) b) . (8)

Обычно число интервалов группировки 9<r<21 . Если распределение предполагается симметричным, то r желательно брать нечетным.

3. Определяются длина и границы интервалов группировки. Для всех 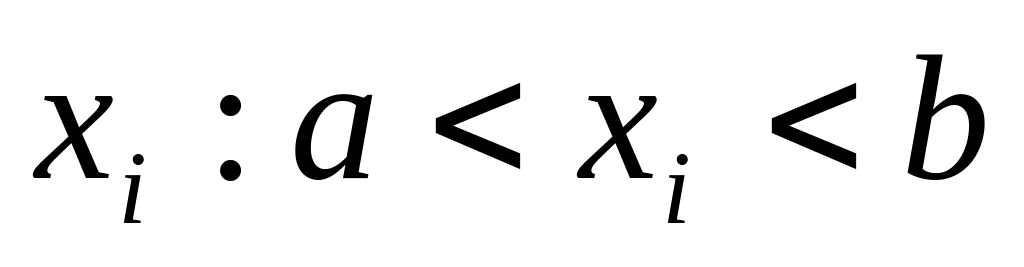, где

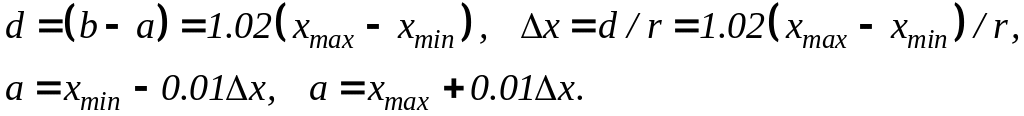
Границы j-ого интервала (9)

Для односторонних распределений (экспоненциального, релеевского, хи-квадрат и др.) а=0.

4. Подсчитывается количество k_j элементов выбор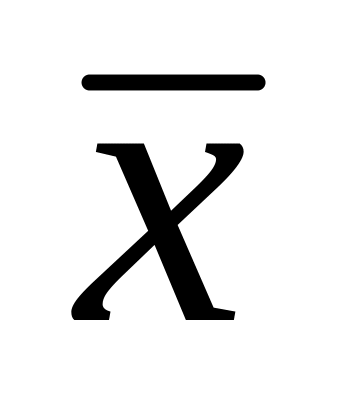ки , попавших в интервал группировки Число .

5. Определяются частоты 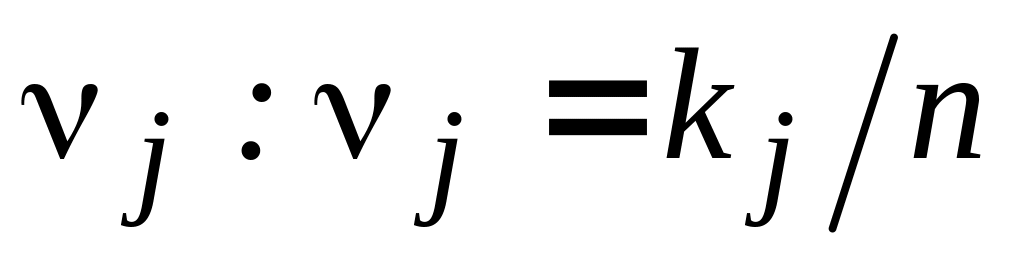(10)

либо относительные частоты и строится диаграмма из столбцов высотой или .

Гистограмма меньше всего отличается от теоретической в центре интервала группировки

III. Правило построения полигона накопленных частот:

Берется выборка и определяется число интервалов группировки так же, как и при построении гистограммы (пункты 1,2,3).

4. Подсчитывается количество К_q элементов выборки , попавших в интервал ,

(11)

4. Определяются выборочные вероятности

(12)

и строится ступенчатая диаграмма, высота которой равна на интервале

Полигон меньше всего отличается от теоретической функции распределения в конце интервала группировки.

IV. Сравнение теоретического и эмпирического распределений

Вероятностная бумага. Вероятностная бумага принадлежит к полукачественному критерию, на основе которого можно судить о соответствии эмпирического распределения и предполагаемого теоретического распределения.

Этапы проверки:

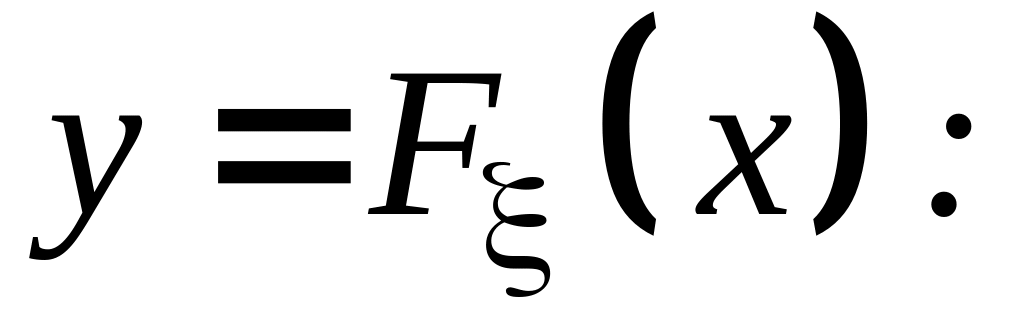
1. Построение обратной функциональной зависимости для функции распределения (13)

2. Построение полигона накопленных частот

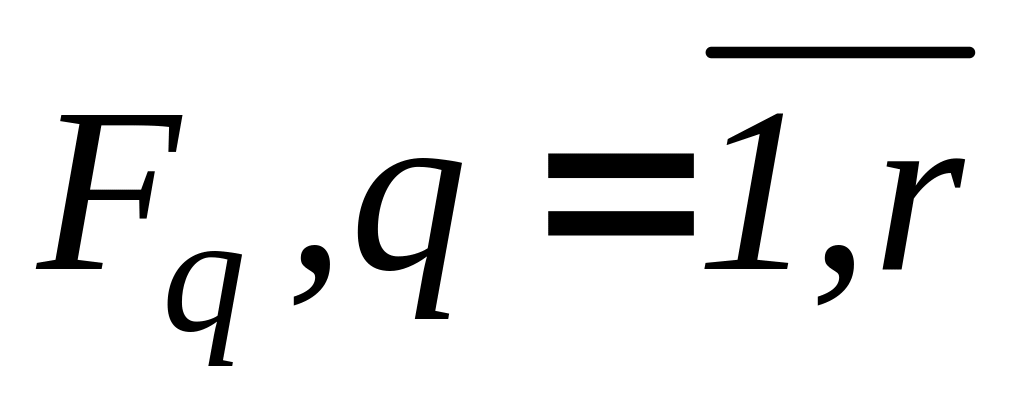
3. Пересчет полигона накопленных частот 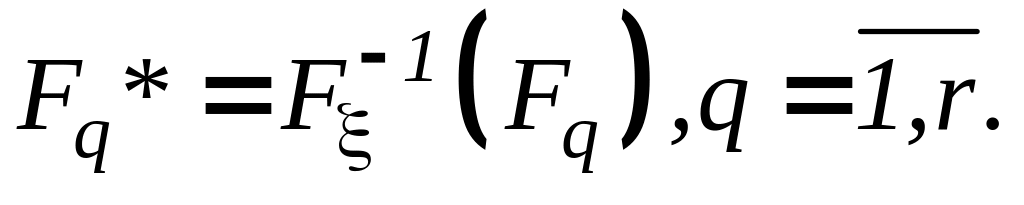(14)

4. Построение в системе координат 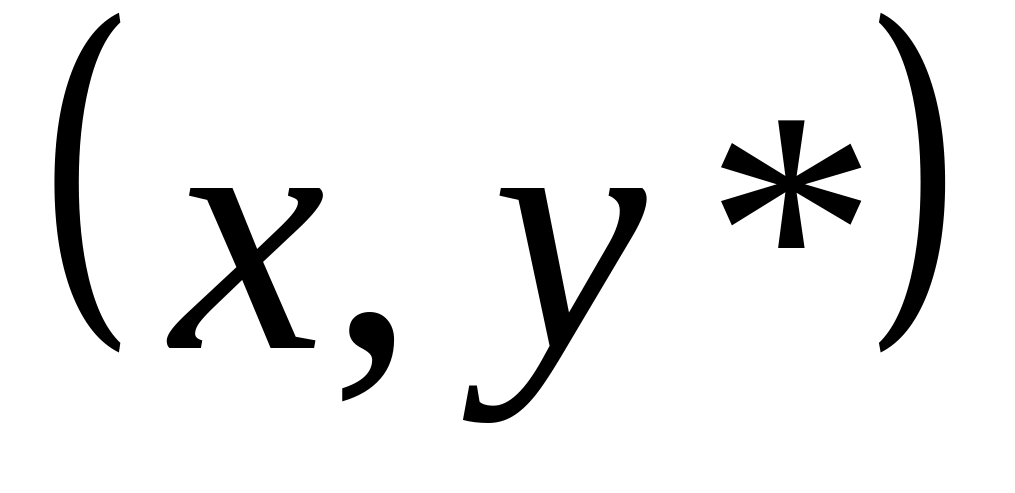графиков по точкам 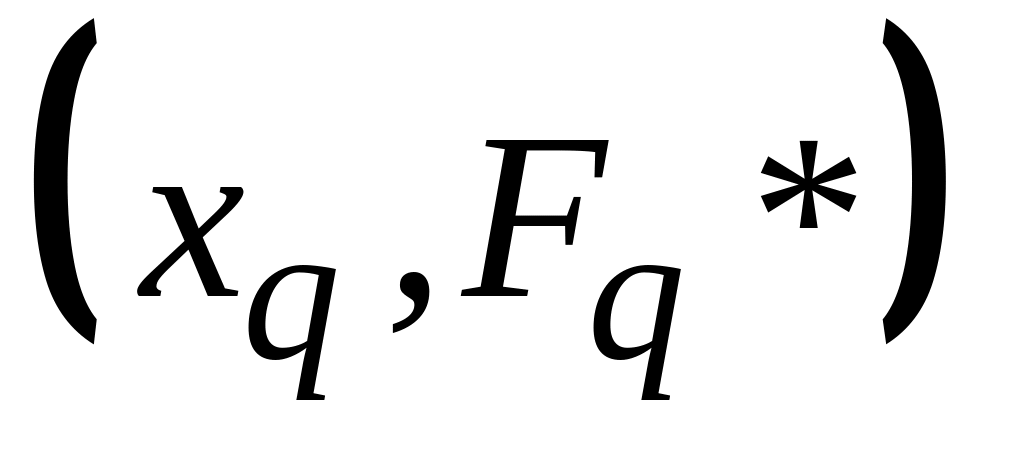, где .

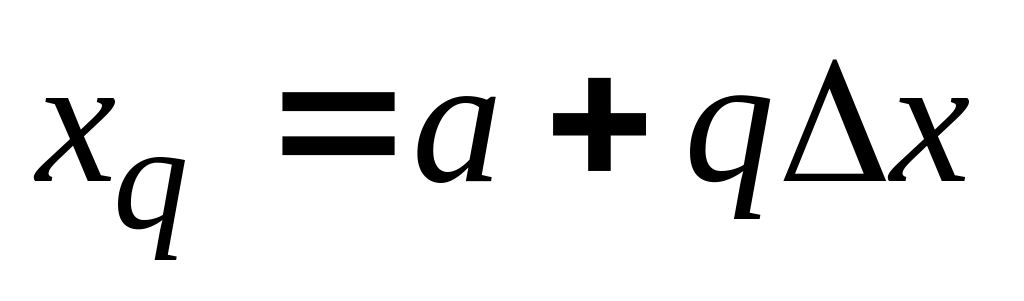5. Если график пересчитанного полигона накопленных частот 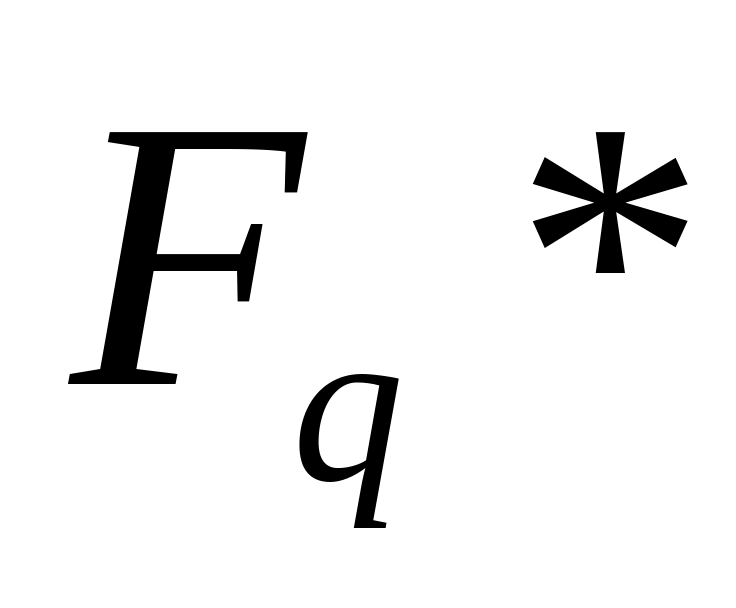- прямая линия, то эмпирическое распределение соответствует , иначе соответствия нет.

Критерий согласия (хи-квадрат) Пирсона. Критерий согласия Пирсона принадлежит к универсальным количественным критериям. С помощью этого критерия можно проверить соответствие теоретического и эмпирического распределений для любого типа случайных величин: непрерывных, дискретных. Он имеет вид:

(15)

Здесь п - объем выборки, r- число интервалов группировки, - частота попадания выборки в интервал - теоретическая вероятность попадания случайной величины в интервал ,

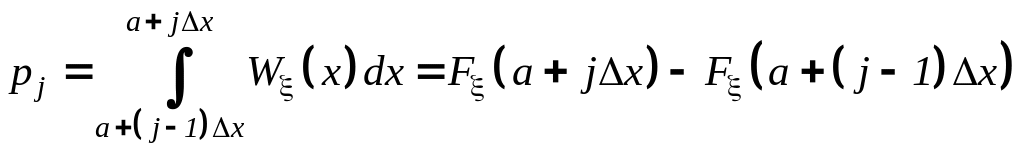
- критическое значение, зависящее от параметров  и l,  - уровень значимости (вероятность отбросить правильную гипотезу о соответствии распределений), - число степеней свободы, где v - количество неизвестных параметров в теоретическом распределении, которые доопределяются по той же выборке .

Например:

1. , где т и  известны (или заданы). Тогда v=0.

2. , где т неизвестно, а  задано. Тогда 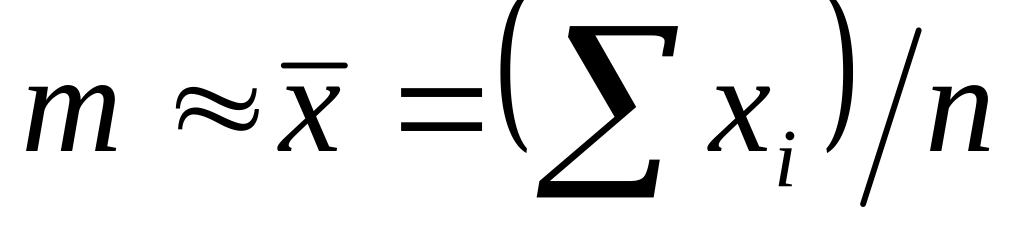и v=1.

3. , где т и  неизвестны. Тогда , 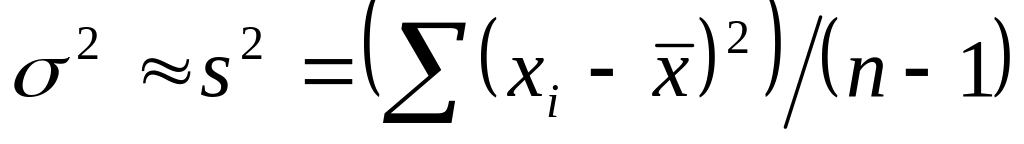и v=2.

Типичные значения уровня значимости =0.1, 0.05, 0.01. Чаще всего =0.1.

Критические значения , являются квантилями вероятностей 1 -  для хи-квадрат распределения с l -степенями свободы - , которые вычисляются при помощи функции Mcad qchisq(1-,l).

Построение гистограмм в системе Mcad

Для построения гистограмм в системе Mcad имеется функция hist(int,X). Здесь Х -выборка из n элементов, int – массив границ интервалов группировки, содержащий r+1 элемент, r - число интервалов группировки. Результатом вычислений этой функции является массив из г элементов k_j,определяющих число элементов выборки из интервала [int_j, int_j+1], j=0..r-1.