
- •Часть I. Mathcad 5
- •Часть II. Maxima. 11
- •Часть III. Лабораторные работы 20
- •Часть I. Mathcad
- •Арифметические вычисления
- •Использование формул в Mathcad
- •Работа с векторами и матрицами
- •Построение графиков в среде Mathcad
- •Чтение и запись данных
- •Знакомство с Mathcad
- •Часть II. Maxima.
- •Интерфейс Maxima.
- •Принципы работы с wxMaxima.
- •Списки.
- •Массивы.
- •Векторы и матрицы.
- •Построение графиков функций.
- •Решение уравнений.
- •Условные выражения и циклы.
- •Чтение и запись данных
- •Часть III. Лабораторные работы лабораторная работа № 1 функциональный масштаб. Интерполяция
- •Интерполяция лагранжа, ньютона.
- •Контрольные задания
- •Примеры выполнения заданий в пакете maxima
- •Лабораторная работа № 2 численное интегрирование
- •Задания.
- •Пример выполнения работы.
- •Лабораторная работа № 3 применение интеграла вероятности для анализа данных
- •Стандартные функции системы mcad
- •Стандартные функции системы Maxima (пакет distrib)
- •Контрольные задания
- •Лабораторная работа № 4 моделирование случайных величин. Метод монте-карло Формирование непрерывных случайных величин
- •Вычисление интегралов методом Монте-Карло
- •Стандартные функции maxima для генерации случайных величин.
- •Задания.
- •Задание “а” (Моделирование выборки)
- •Задание “в” (Выборка из файлов данных)
- •2. Выборочные распределения
- •Задание “a” (Моделирование выборки)
- •Лабораторная работа № 6 метод наименьших квадратов
- •Задания
- •Приложение Некоторые встроенные функции Mathcad
- •Основные законы распределения
- •Литература
- •Составители: Радченко Юрий Степанович
Вычисление интегралов методом Монте-Карло
Метод
1.0  ,
где
,
где
![]()
Здесь n-
число испытаний,
![]() -независимые
стандартные равномерно распределенные
на интервале [0,1] случайные числа.
-независимые
стандартные равномерно распределенные
на интервале [0,1] случайные числа.
Метод
2.0 ![]() ,
,
где k-
количество событий
![]() в n
испытаниях,
имеет плотность вероятности
в n
испытаниях,
имеет плотность вероятности
![]() .
формируется из
путем соответствующего нелинейного
преобразования на основе метода обратных
функций или метода Неймана.
.
формируется из
путем соответствующего нелинейного
преобразования на основе метода обратных
функций или метода Неймана.
Метод
3.0. Пусть
функция f(x)
вписана в прямоугольник: a<x<b,
0<y<M.
Формируем пару равномерно распределенных
чисел
![]() ,
рассматривая их как координаты случайной
точки в прямоугольнике. Затем подсчитываем
количество точек k,
попавших под кривую f(x),
т.е. при выполнении условия
,
рассматривая их как координаты случайной
точки в прямоугольнике. Затем подсчитываем
количество точек k,
попавших под кривую f(x),
т.е. при выполнении условия
![]() в n
испытаниях. Тогда
в n
испытаниях. Тогда
![]()
Стандартные функции maxima для генерации случайных величин.
random(А) — формирует псевдослучайное число, равномерно распределенное между 0 и А. Тип генерируемых значений (целый или вещественный) совпадает с типом аргумента А.
random_normal(m,s) формирует гауссовскую случайную величину с математическим ожиданием m и среднеквадратическим отклонением s;
random_normal(m,s,n) формирует n гауссовских случайных величин с математическим ожиданием m и среднеквадратическим отклонением s.
random_chi2(n,m)
формирует m
случайных величин с законом распределения
![]() с n
степенями свободы.
с n
степенями свободы.
random_exp(,m) формирует m случайных величин с экспоненциальным законом распределения с n степенями свободы.
random_gamma(с,1,n) формирует n случайных величин с гамма распределением, с — параметр формы.
random_poisson (,n) формирует n случайных величин с пуассоновским распределением.
random_binomial(k,p,m) формирует m случайных величин с биномиальным распределением.
Задания.
Сформировать гауссовский случайный процесс из 200 независисмых случайных чисел. Построить график процесса. Найти матожидание и дисперсию процесса.
Сформировать релеевский процесс из 100 независимых случайных чисел согласно алгоритму =
 .
Вычислить первый и второй начальные
моменты и сравнить с теоретическими
значениями.
.
Вычислить первый и второй начальные
моменты и сравнить с теоретическими
значениями.Сформировать процесс с распределением, используя функцию rchisq(NN,n), где NN=100 объем выборки, n – число степеней свободы. Вычислить мат. ожидание и дисперсию процесса, сравнить их с теоретическими значениями.
Сформировать процесс с экспоненциальным распределением, используя функцию rexp(NN, ) (randon_exp(,NN)). NN - объем выборки, - параметр распределения. (=1, 2) . Вычислить мат. ожидание и дисперсию процесса, сравнить их с теоретическими значениями.
Сформировать процесс с n распределением согласно алгоритму
 , kN(0,1).
Вычислить первый и второй начальные
моменты и сравнить с теоретическими
значениями.
, kN(0,1).
Вычислить первый и второй начальные
моменты и сравнить с теоретическими
значениями.Сформировать процесс с гамма-распределением при различных значениях параметра “с”.
Сформировать 100 значений пуассоновской случайной величины с параметром =0.4, 1, 8
Сформировать 100 значений биномиальной случайной величины с параметрами p=0.4, k=4, 20, 100.
Вычисление интегралов методом Монте-Карло.
1.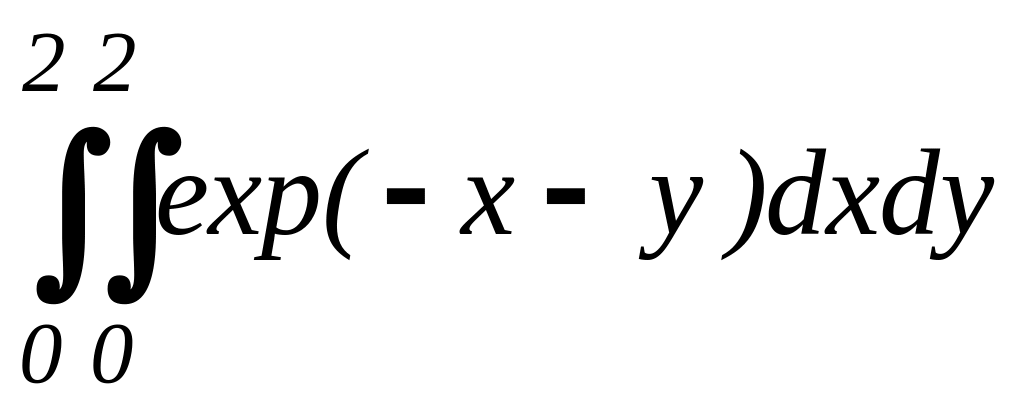 ;
2.
;
2. ;
3.
;
3.![]()
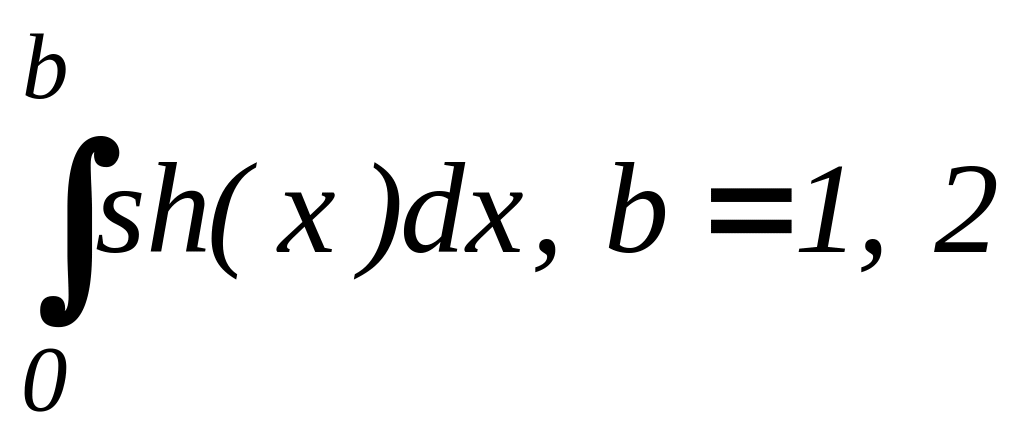 ;
4.
;
4. ;
5.
;
5.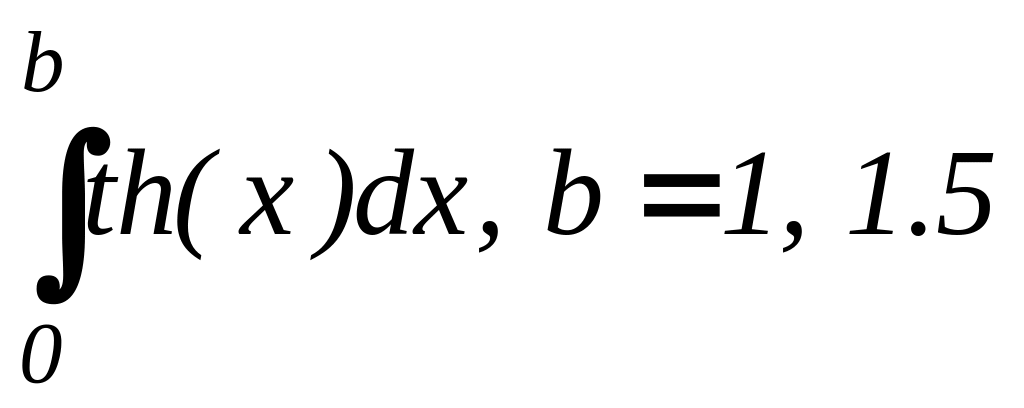 ;
6.
;
6.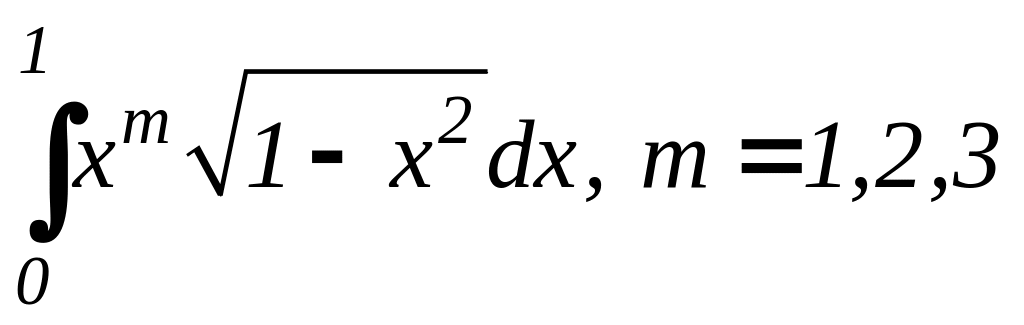 ;
7.
;
7.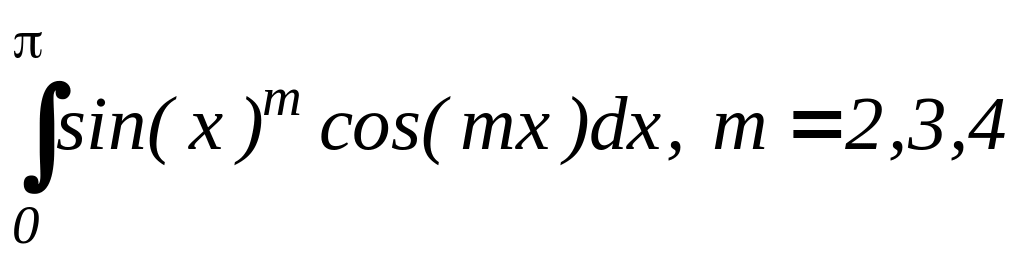 ;
8.
;
8.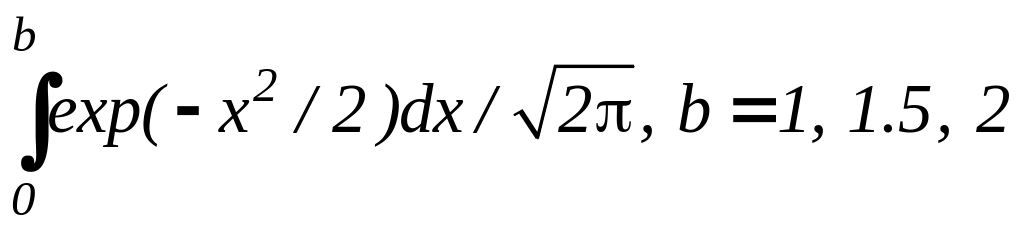 ;
9.
;
9. .
.
Пример выполнения заданий
Сформировать гауссовский случайный процесс из 200 независисмых случайных чисел. Построить график процесса. Найти матожидание и дисперсию процесса
load(distrib);
N:1000;
x:random_normal(0,1,N)$
или
x:makelist(sum(random(1.0),k,1,12)-6,i,1,N)$
t:makelist(i,i,1,N)$
wxplot2d([discrete,t,x]);
m:sum(x[i],i,1,N)/N;
d:sum((x[i])^2,i,1,N)/(N);
ЛАБОРАТОРНАЯ РАБОТА № 5
ПЕРВИЧНАЯ ОБРАБОТКА ДАННЫХ
1. ВЫБОРОЧНЫЕ МОМЕНТЫ. РАСЧЕТ ПОГРЕШНОСТЕЙ
ОБЩИЕ СООТНОШЕНИЯ.
Набор значений
![]() измеряемой
величины
измеряемой
величины
![]() ,
полученный при п
-кратном повторении эксперимента,
называется реализацией выборки. Можно
считать, что все возможные реализации
составляют случайную выборку
,
полученный при п
-кратном повторении эксперимента,
называется реализацией выборки. Можно
считать, что все возможные реализации
составляют случайную выборку
![]() .:
Оценкой
.:
Оценкой
![]() параметра
называется
некоторая статистика (функция выборки)
параметра
называется
некоторая статистика (функция выборки)
![]() ,
приближенно соответствующая ,
и при объеме
выборки
,
приближенно соответствующая ,
и при объеме
выборки
![]() сходящаяся (в вероятностном смысле) к
истинному значению параметра. Случайная
оценка
сходящаяся (в вероятностном смысле) к
истинному значению параметра. Случайная
оценка
![]() может
быть охарактеризована следующими
числовыми значениями:
может
быть охарактеризована следующими
числовыми значениями:
средним значением оценки:

смещением оценки:
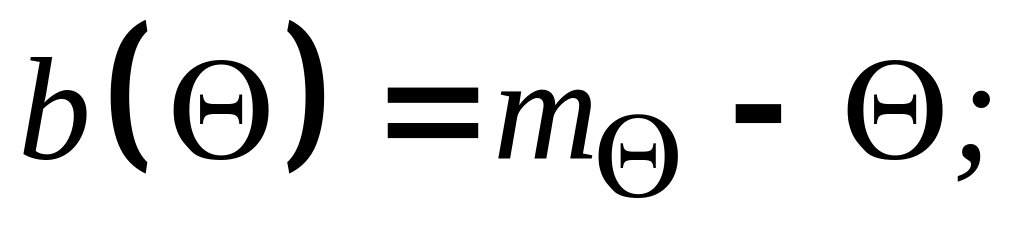
дисперсией оценки:
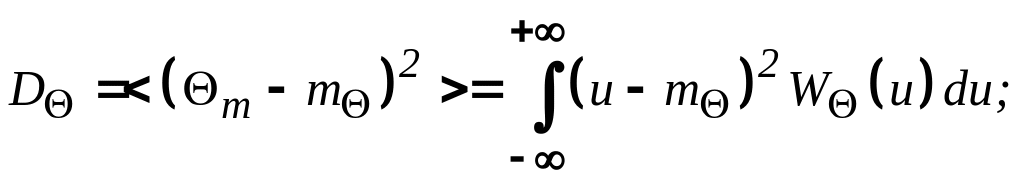
доверительной вероятностью Р0 и доверительным интервалом ,
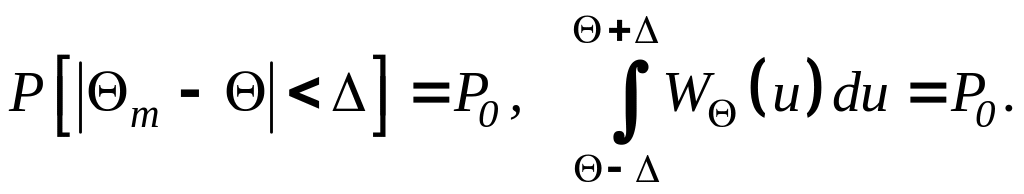 Здесь
Здесь
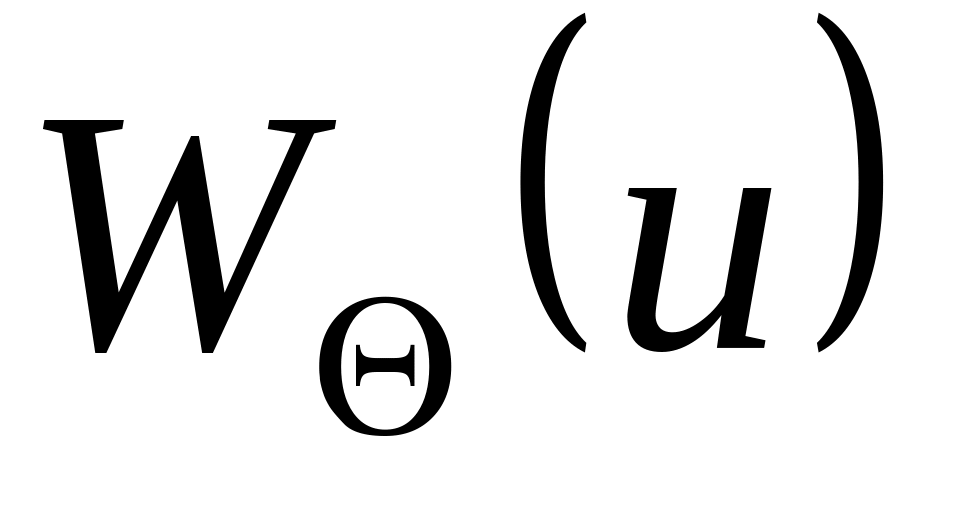 -
плотность вероятности оценки.
-
плотность вероятности оценки.
ОСНОВНЫЕ ПАРАМЕТРЫ И ХАРАКТЕРИСТИКИ ОЦЕНОК
Параметр
 - математическое ожидание:
- математическое ожидание:
Оценка:
 (1)
(1)
смещение
оценки:
![]() дисперсия оценки:
дисперсия оценки:
![]() распределение
оценки – нормальное, т.е.
распределение
оценки – нормальное, т.е.
![]() доверительный интервал:
доверительный интервал:
![]() ,
где
,
где
![]()
Параметр
 -
дисперсия:
-
дисперсия:математическое ожидание известно
Оценка:
 (2)
(2)
смещение:
дисперсия:
![]() распределение:
распределение:
![]() -
хи-квадрат (при n>100
– асимптотически нормальное);
асимптотически доверительный интервал
-
хи-квадрат (при n>100
– асимптотически нормальное);
асимптотически доверительный интервал
![]() где
.
где
.
математическое ожидание неизвестно
Оценка
 (3)
(3)
смещение:
дисперсия:
![]() распределение:
распределение:
![]() (при n>100
– асимптотически нормальное)
(при n>100
– асимптотически нормальное)
Параметр mk - начальный момент k-ого порядка:
Оценка:
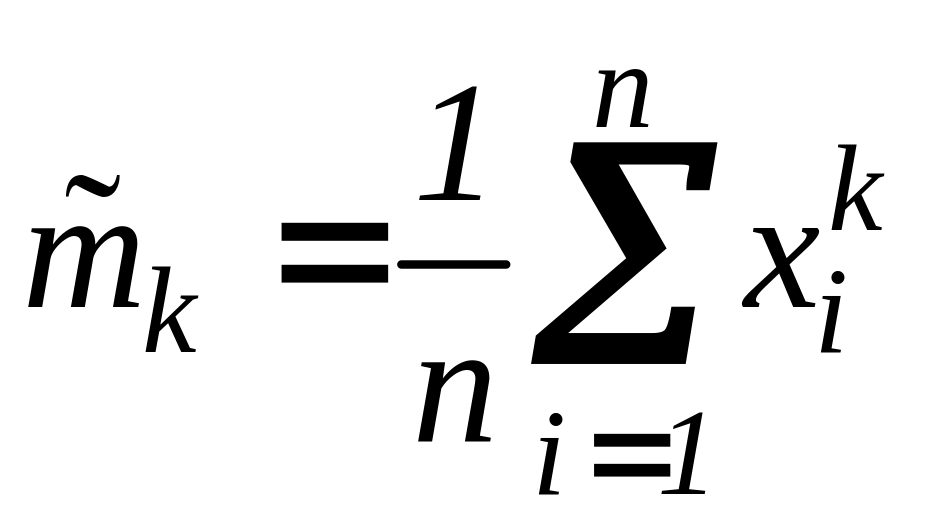 (4)
(4)
смещение:
дисперсия:
![]() .
.
Параметр - выборочный центральный момент k-ого порядка
Оценка:
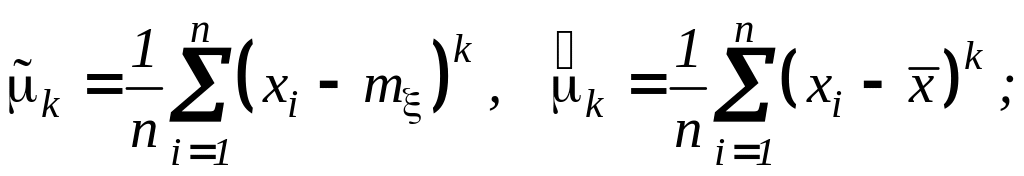 (5)
(5)
смещение:
![]() - несмещенная,
- несмещенная,
![]() -
асимптотически несмещенная.
-
асимптотически несмещенная.
5. Связь
![]() и
при k=2,3,4
и
при k=2,3,4
![]() (6)
(6)
6.Параметр -
выборочные коэффициенты асимметрии
![]() и эксцесса
и эксцесса
![]()
![]() (7)
(7)
