
- •Часть I. Mathcad 5
- •Часть II. Maxima. 11
- •Часть III. Лабораторные работы 20
- •Часть I. Mathcad
- •Арифметические вычисления
- •Использование формул в Mathcad
- •Работа с векторами и матрицами
- •Построение графиков в среде Mathcad
- •Чтение и запись данных
- •Знакомство с Mathcad
- •Часть II. Maxima.
- •Интерфейс Maxima.
- •Принципы работы с wxMaxima.
- •Списки.
- •Массивы.
- •Векторы и матрицы.
- •Построение графиков функций.
- •Решение уравнений.
- •Условные выражения и циклы.
- •Чтение и запись данных
- •Часть III. Лабораторные работы лабораторная работа № 1 функциональный масштаб. Интерполяция
- •Интерполяция лагранжа, ньютона.
- •Контрольные задания
- •Примеры выполнения заданий в пакете maxima
- •Лабораторная работа № 2 численное интегрирование
- •Задания.
- •Пример выполнения работы.
- •Лабораторная работа № 3 применение интеграла вероятности для анализа данных
- •Стандартные функции системы mcad
- •Стандартные функции системы Maxima (пакет distrib)
- •Контрольные задания
- •Лабораторная работа № 4 моделирование случайных величин. Метод монте-карло Формирование непрерывных случайных величин
- •Вычисление интегралов методом Монте-Карло
- •Стандартные функции maxima для генерации случайных величин.
- •Задания.
- •Задание “а” (Моделирование выборки)
- •Задание “в” (Выборка из файлов данных)
- •2. Выборочные распределения
- •Задание “a” (Моделирование выборки)
- •Лабораторная работа № 6 метод наименьших квадратов
- •Задания
- •Приложение Некоторые встроенные функции Mathcad
- •Основные законы распределения
- •Литература
- •Составители: Радченко Юрий Степанович
Стандартные функции системы mcad
cnorm(x)
– вычисляет интеграл вероятностей
![]()
pnorm(x,,)
вычисляет функцию распределения
![]()
erf(x) вычисляет
функцию
ошибок
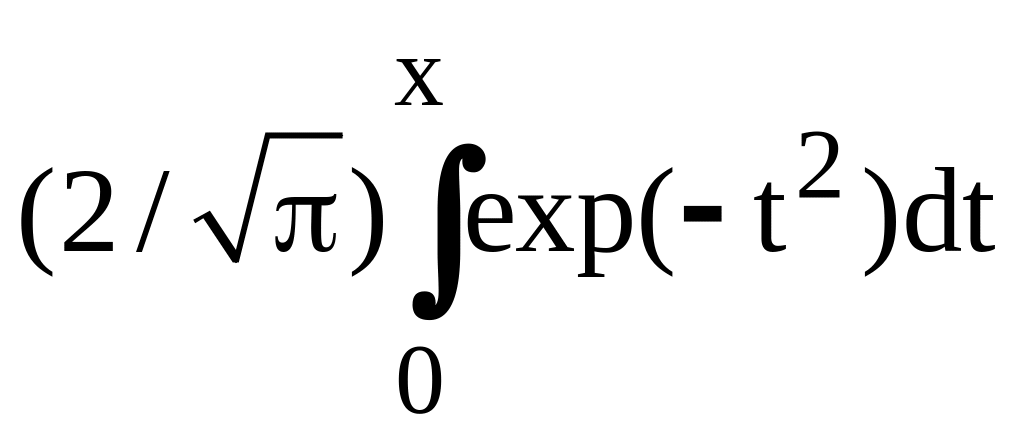
dnorm(x,,)
– вычисляет
![]()
qnorm(p,,)-вычисляет
квантиль нормального закона с параметрами
(,)
для вероятности р . Квантиль распределения
порядка р является решением уравнения
F(xq)=((xq-)/)=p.
Вычисляет обратную функцию к
![]()
Стандартные функции системы Maxima (пакет distrib)
load(distrib) — загружает пакет distrib;
cdf_normal(x,
,)
– вычисляет
функцию распределения
![]() .
.
erf(x) – вычисляет функцию ошибок
pdf_normal (x,,) – вычисляет
quantile_normal(p,,) – вычисляет квантиль нормального закона с параметрами (,) для вероятности р . Квантиль распределения порядка р является решением уравнения F(xq)=((xq-)/)=p. Вычисляет обратную функцию к .
Контрольные задания
Запрограммировать вычисление по формуле (6), (7).
Запрограммировать вычисление по формуле (8).
Сравнить вычисление интеграла вероятности при помощи функции cnorm(x), аппроксимации (6) и асимптотической формулы (8). Построить графики различных представлений 1-(х) в диапазоне 1<x<8 в логарифмическом масштабе.
Сформировать реализацию из 100 гауссовских чисел, используя функцию rnorm(n,,), построить график этой реализации.
Задачи
Для стандартной гауссовской случайной величины
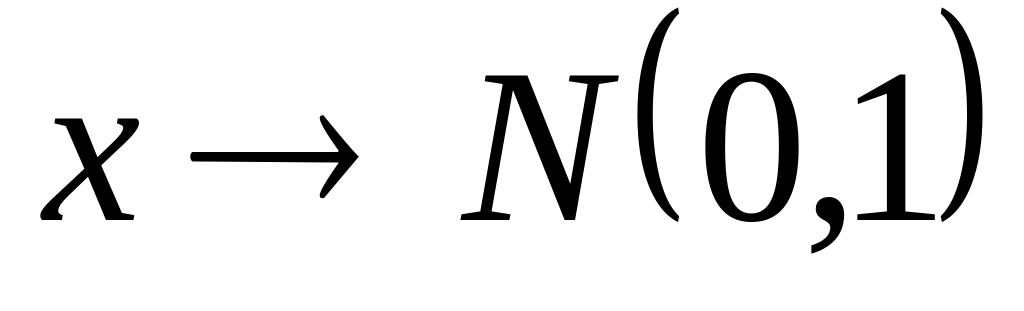 вероятность какого из неравенств больше
вероятность какого из неравенств больше
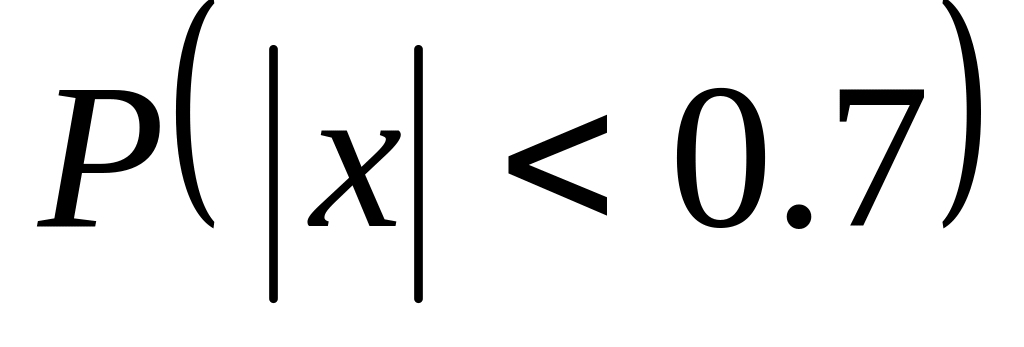 или
или
 .
.Генератор шума вырабатывает гауссовский случайный процесс с параметрами m=0 и
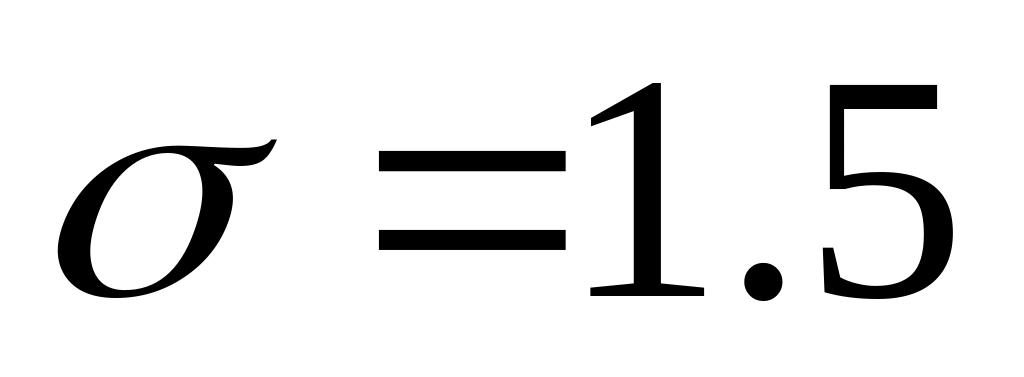 вольта. Чему равна вероятность того,
что мгновенные значения шума находятся
в интервале [-1.5 в; +1.5 в], [-3 в; +3 в], [-4.5 в;
+4.5 в].
вольта. Чему равна вероятность того,
что мгновенные значения шума находятся
в интервале [-1.5 в; +1.5 в], [-3 в; +3 в], [-4.5 в;
+4.5 в].На пороговое устройство с напряжением срабатывания h вольт подается гауссовский шум с параметрами т=0.2 в и
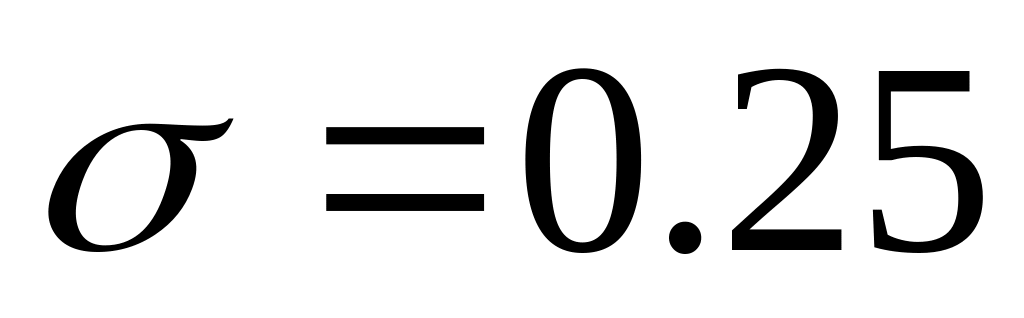 в. Рассчитать вероятность превышения
мгновенными отсчетами шума порогового
уровня 0.2<h<2.5
v.
в. Рассчитать вероятность превышения
мгновенными отсчетами шума порогового
уровня 0.2<h<2.5
v.Рассчитать вероятность пропуска (А) импульса с амплитудой А, лежащей в диапазоне, 0.4<А<=1.5 v, который поступает вместе с шумом с параметрами т=0 и
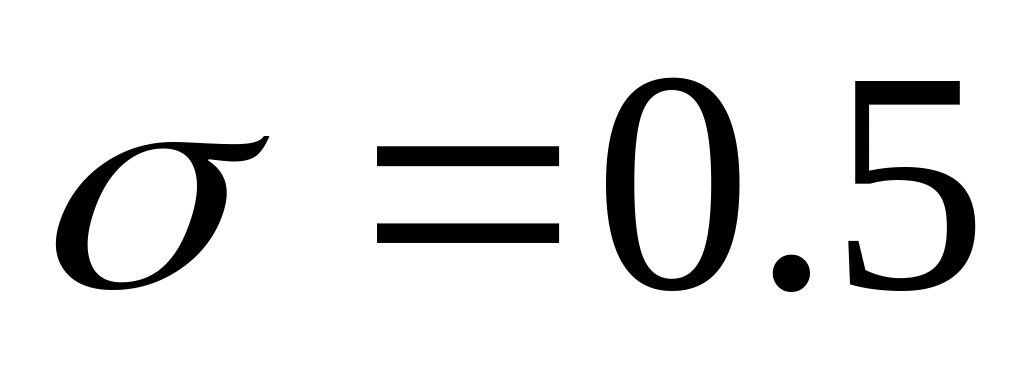 в на пороговое устройство с уровнем
срабатывания 0.6 в. Построить зависимость
(А),
проследить динамику этой ошибки при
различных .
в на пороговое устройство с уровнем
срабатывания 0.6 в. Построить зависимость
(А),
проследить динамику этой ошибки при
различных .Вероятность ложной тревоги при обнаружении на интервале, содержащем «m» элементов разрешения, определяется выражением
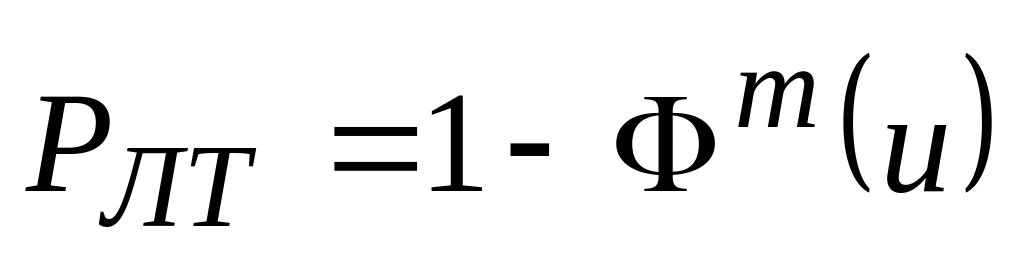 .
Рассчитайте вероятность ложной тревоги
для
.
Рассчитайте вероятность ложной тревоги
для
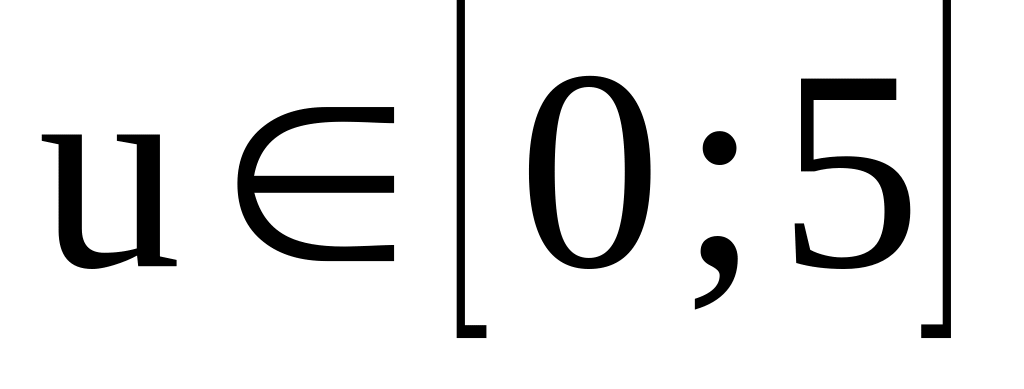 при значениях m=1,
10, 20.
при значениях m=1,
10, 20.Вероятность ошибки различения неортогональных видеосигналов определяется формулой
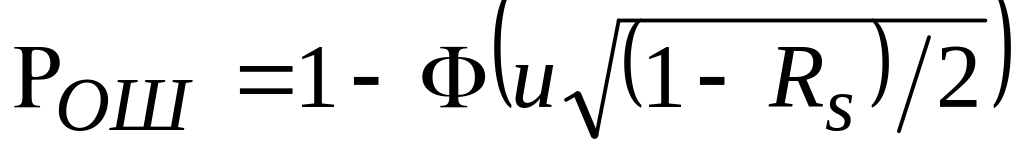 .
Рассчитайте зависимость
.
Рассчитайте зависимость
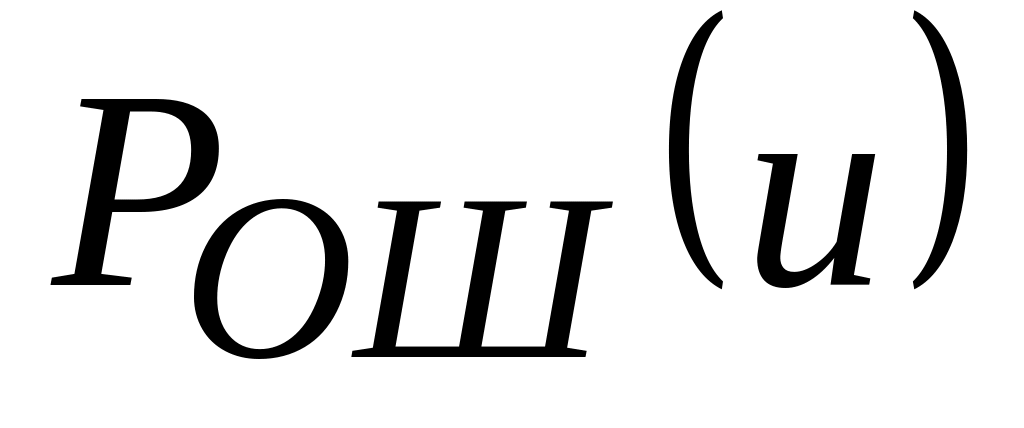 для
для
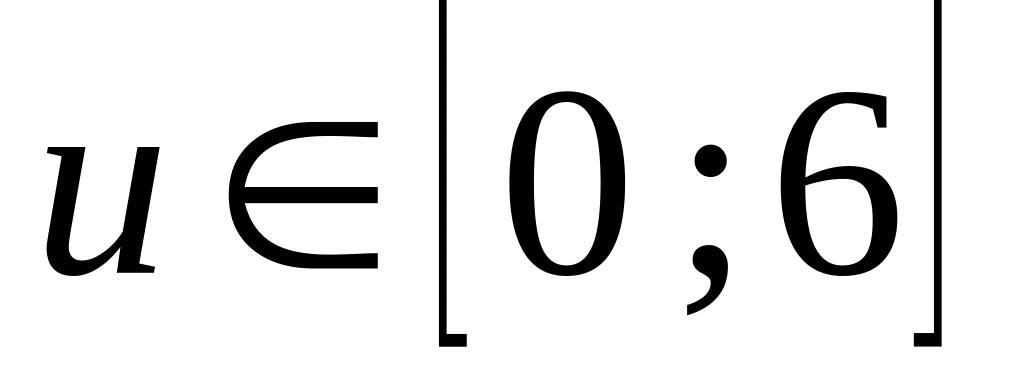 при значениях RS
=0.2, 0.5, 0.8.
при значениях RS
=0.2, 0.5, 0.8.Ошибка различения M сигналов с системе связи определяется формулой
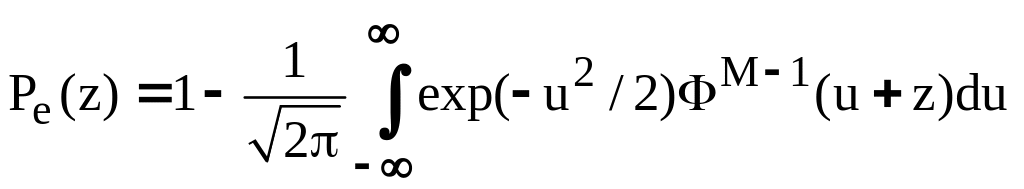 .
Заменяя
.
Заменяя
 числовым значением 5, исследуйте Pe(z)
в диапазоне 0< z<6
при разных M
( М=2,3,5,10)
числовым значением 5, исследуйте Pe(z)
в диапазоне 0< z<6
при разных M
( М=2,3,5,10)Найти квантиль гауссовского распределения, соответствующий вероятности
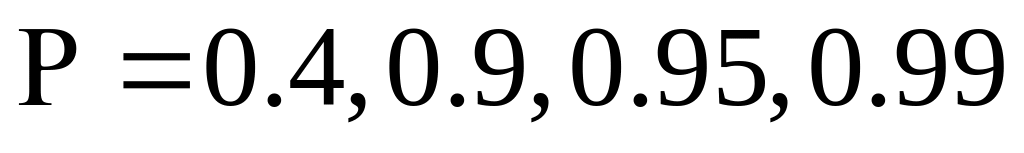 при m=1,
=1,
1.5
при m=1,
=1,
1.5Построить и проанализировать двумерную гауссовскую плотность вероятности
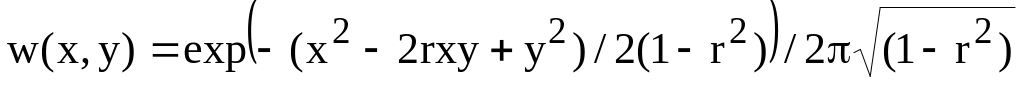 в
диапазоне
в
диапазоне
{–2<x,y<2}
Лабораторная работа № 4 моделирование случайных величин. Метод монте-карло Формирование непрерывных случайных величин
Имеется несколько методов формирования непрерывных случайных величин из равномерных и гауссовских чисел.
Метод обратных функций. Если необходимо сформировать случайную величину с функцией распределения F(x), то используется преобразование базового равномерно распределенного числа [0,1] вида
![]() ,
,
где
![]() -функция,
обратная к функции распределения.
-функция,
обратная к функции распределения.
Пример: Сформировать
релеевскую случайную величину
с плотностью вероятности 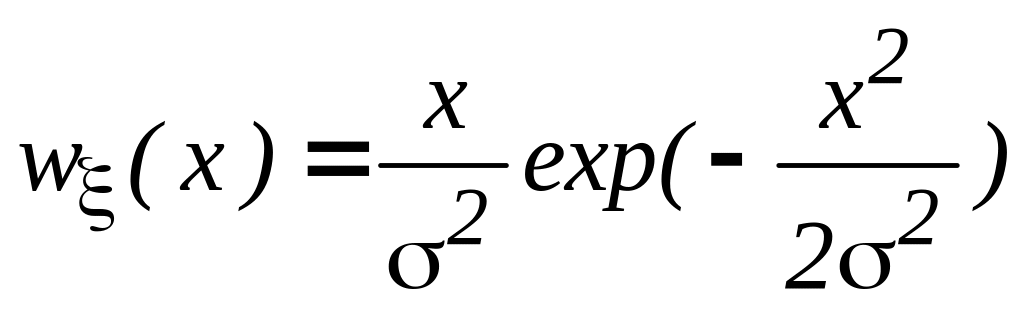 .
.
Решение:
![]() .
Уравнение для нахождения
имеет вид
.
Уравнение для нахождения
имеет вид
![]() .
Его решение
.
Его решение
![]() .
Здесь учтена статистическая эквивалентность
величин
и 1-.
.
Здесь учтена статистическая эквивалентность
величин
и 1-.
Метод Неймана (метод исключения). Пусть
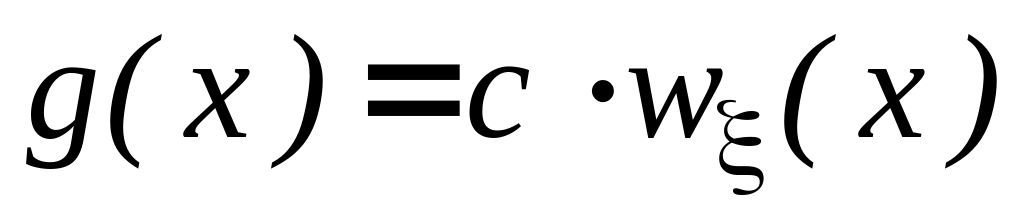 ,
где С- некоторая константа, a<x<b,
g(x)<M.
Кривая g(x)
вписана, таким образом, в прямоугольник.
Формируем два равномерно распределенных
числа
,
где С- некоторая константа, a<x<b,
g(x)<M.
Кривая g(x)
вписана, таким образом, в прямоугольник.
Формируем два равномерно распределенных
числа
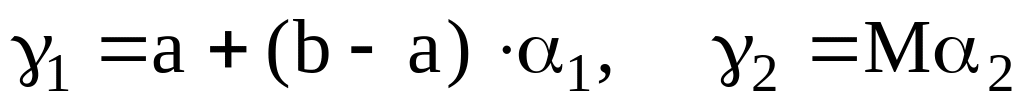 ,
которые рассматриваются как координаты
случайной точки в этом прямоугольнике.
Если
,
которые рассматриваются как координаты
случайной точки в этом прямоугольнике.
Если
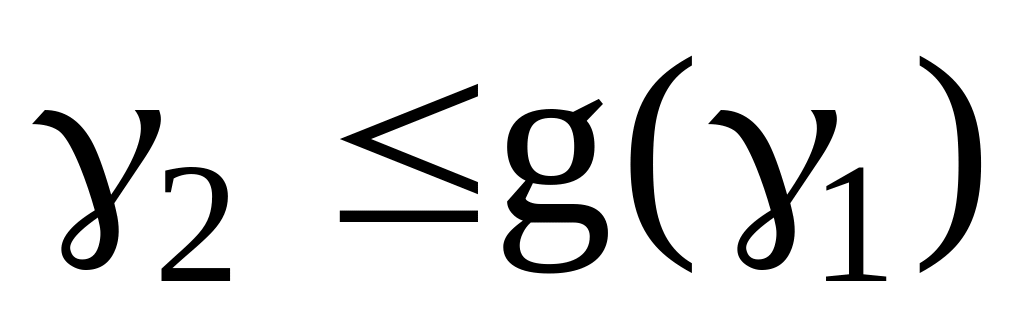 ,
то есть точка лежит под кривой, то
,
то есть точка лежит под кривой, то
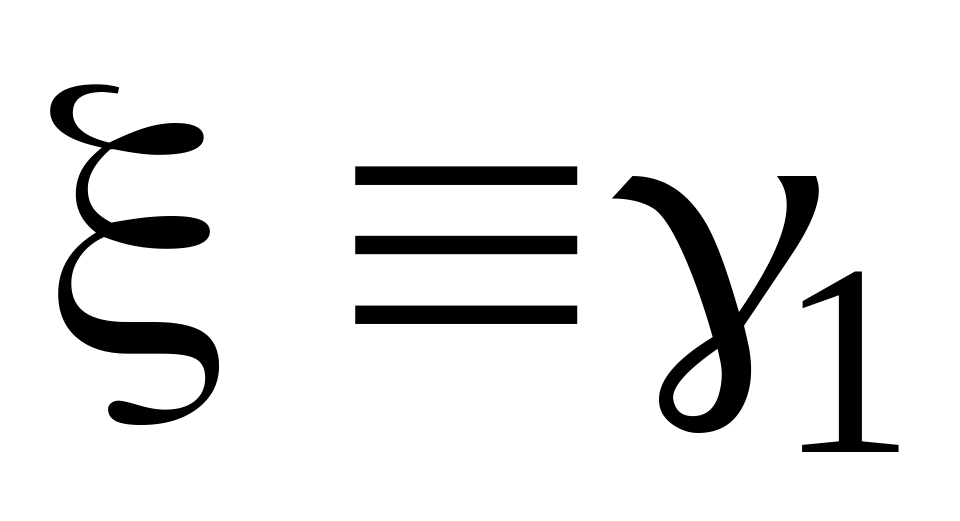 .
Иначе эта точка отбрасывается.
.
Иначе эта точка отбрасывается.
Пример. Сформировать
случайную величину
с плотностью вероятности ![]() .
.
Решение: g(x)=cos(2x),
![]() .
Если
.
Если
![]() ,
то
,
то
![]() .
.
Формирование случайных величин с
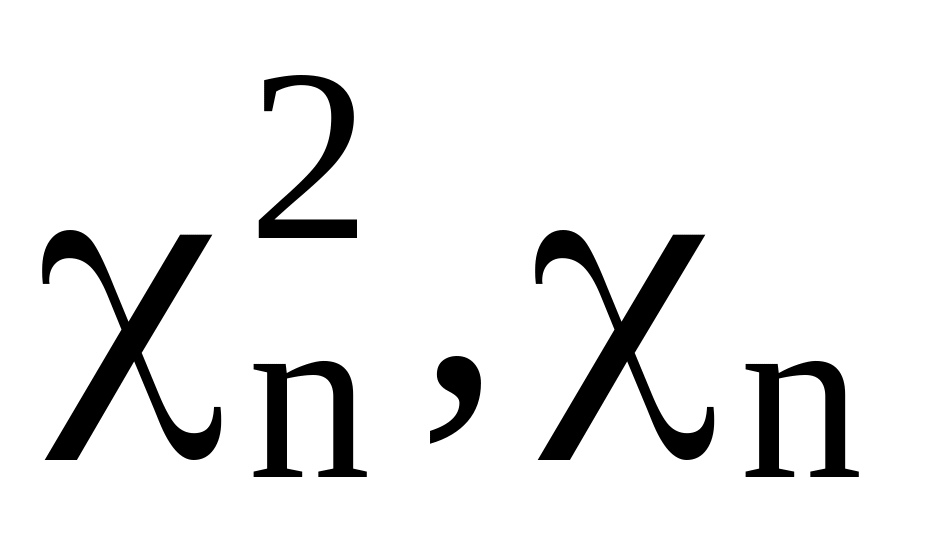 законами распределения.
законами распределения.
Пусть
![]() независимые
нормально распределенные случайные
величины с параметрами m=0,=1.
Тогда
независимые
нормально распределенные случайные
величины с параметрами m=0,=1.
Тогда
![]() ,
, ![]() .
.
Формирование стандартных гауссовских случайных величин на основе центральной предельной теоремы. Алгоритм
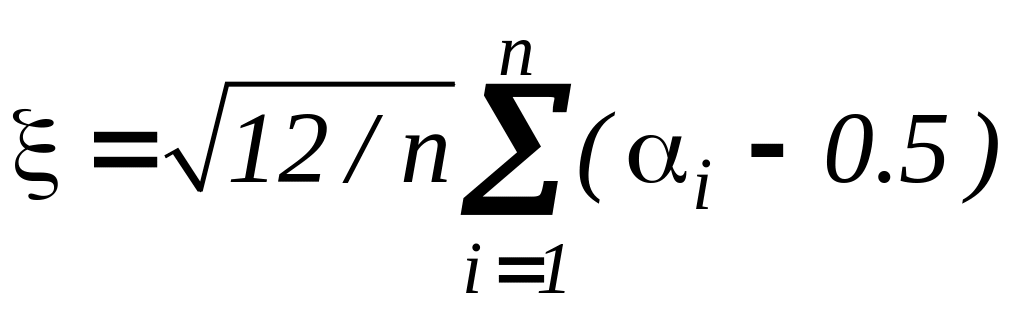
формирует случайное
число с распределением, близким к
нормальному. Частным случаем его является
алгоритм
![]() .
Хорошим качеством случайных чисел
обладает метод суммирования 5 чисел с
поправкой
.
Хорошим качеством случайных чисел
обладает метод суммирования 5 чисел с
поправкой
![]() .
.
