2. Аналитическое дифференцирование средствами matlab.

В лабораторной работе, основной задачей которой является исследование методов численного интегрирования, для отыскания теоретической погрешности результатов требуется знание производной от интегрируемой функции до четвертого порядка включительно.

Для вычисления производных аналитически в MATLAB спользуется функция diff.

Синтаксис:

Вызов	Описание
diff(S)	Вычисляется аналитическое выражение для производной от функции S, заданной символьно.
diff(S,n)	Вычисляется аналитическое выражение для производной от функции S порядка n.

Пример использования функции diff при вычислении максимума второй производной на отрезке [a, b]

График производной:

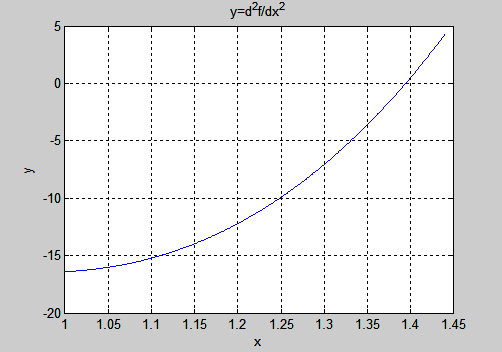
3. Теоретическая оценка погрешности численного интегрирования

Рассмотрим примеры использования теоретической оценки погрешности интегрирования на примере двух задач.

Задача 1. Определить теоретическую погрешность численного интегрирования методом трапеций в случае одного элементарного отрезка интегрирования..

Теоретическая погрешность для метода трапеций составляет

В случае элементарного отрезка иртегрирования, если заданы пределы интегрирования и подинтегральная функция, задачу можно решить например следующим образом:

В результате получим

f2 = 50*x^3-366/5*x^2+34/5 M2 = 16.4000 Погрешность R = 0.1164

Т.о. теоретическая оценка абсолютной погрешности погрешности составляет 0.1. В задаче 1 лабораторной работы вам предлагается убедиться, что данная теоретическая оценка действительно справедлива.

Задача 2. Определить шаг дискретизации и количество узлов интегрирования, необходимые для того. чтобы погрешность интегрирования не превышала величины 0.0001.

Если заданы пределы интегрирования и интегрируемая функция, задачу можно решить например следующим образом:

В результате получим:

f2 = 50*x^3-366/5*x^2+34/5 M2 = 16.4000 h = 1.289562396771206e-002 n = 3.412010160203707e+001 n = 35 h = 1.257142857142857e-002

Таким образом, чтобы вычислить интеграл от функции

f(x)=2.5*x⁵-6.1*x⁴+3.4*x²-9.1*x+18

по методу трапеций c точностью 0.0001, небходимо задать 35 узлов интегрирования. При этом шаг дискретизации составляет h=1.257142857142857*10^-2 .

Вам остается убедиться, что погрешность интегрирования с данными параметрами действительно не превышает 0.0001.

4. Численное интегрирование

Вычислительные формулы приведены в приложении . Их анализ показывает, что формулы для одного элементарного отрезка интегрирования не требуют каких либо новых знаний. Необходимо только приготовить m-функцию, в которой следует определить интегрируемую функцию. И конечно для оценки погрешности интегрирования следует знать точное значение интеграла (см. выше).

Случай формул для составного отрезка интегрирования более сложный. Здесь требуется вычислять значения сумм. Например в методе Симпсона

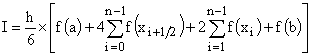
где

В языке программировани MATLAB, как и в других языках программирования, существует оператор цикла for , возможностей которого достаточно для решения поставленных задач. Синтаксис оператора цикла описан в разделе Программирование. Далее мы просто рассмотрим пример решения задачи численного интегрирования.

Пример. Численное интегрирование методом Симпсона.

Закрашенную область следует выполнить самостоятельно

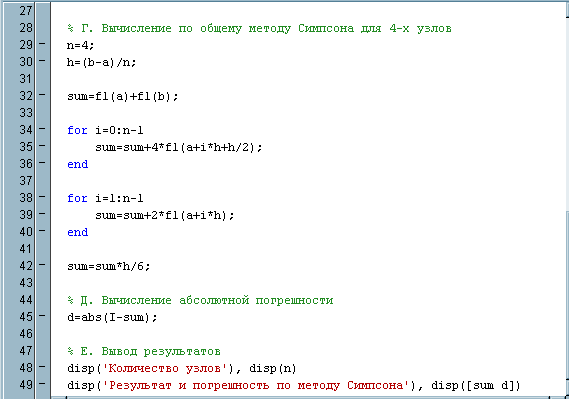
Результаты:

>> Результаты Точное значение интеграла 2.575860114624924e-001 Результат и погрешность для элементарного отрезка 2.575665708043314e-001 1.944065816106289e-005 Количество узлов 4 Результат и погрешность по методу Симпсона 2.575859351120611e-001 7.635043136611230e-008

Конечно, рассматриваемый здесь способ решения задачи является не единственным и не наилучшим. В частности, можно было бы создать m-функцию, в которой и производилось бы вычисление интеграла.