Глава 4. Элементы электрической цепи переменного тока. Временные и векторные диаграммы токов и напряжений на элементах r, l и c.

Если напряжение подключить к сопротивлению R, то через сопротивление потечет ток

(4.1)

Мы видим, что напряжение на сопротивлении и протекающий через него ток совпадают по фазе (фаза  одна и та же у тока и у напряжения). В комплексной форме (4.1) имеет вид:

(4.2)

Комплексному выражению (4.2) соответствует векторная диаграмма на комплексной плоскости (рис. 4.1)

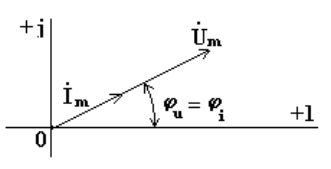
Рисунок 4.1. Векторная диаграмма на комплексной плоскости комплексных амплитуд тока и напряжения , соответствующая синусоидальным току i и напряжению u с амплитудами , ,соответственно, частотой ω и равными начальными фазами φ_i и φ_u.

Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению.

Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току - активным сопротивлением.

Рассмотрим идеальную индуктивную катушку, активное сопротивление R которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции:

(4.3)

Эта ЭДС уравновешивается напряжением, подключенным к катушке так, что: u = e_L, тогда можно записать:

(4.4)

Из (4.4) следует, что ток в индуктивности отстает по фазе от напряжения на 90º из-за явления самоиндукции. Уравнение вида (4.4) для реальной катушки с активным сопротивлением R будет иметь вид:

(4.5)

Анализ выражения (4.5) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0º< φ < 90º), величина которого зависит от соотношения R и L. Выражение (4.5) в комплексной форме записи имеет вид:

(4.6)

где - полное комплексное сопротивление индуктивной катушки ( ), - модуль полного комплексного сопротивления катушки ( ),  - начальная фаза комплексного сопротивления ( ), - индуктивное сопротивление. Для идеальной катушки, естественно, R=0, комплексное сопротивление равно Уравнению (4.6) соответствует векторная диаграмма (рис. 4.2)

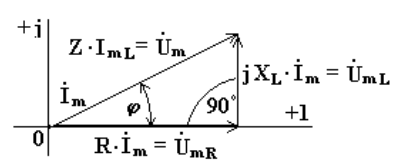
Рисунок 4.2. Векторная диаграмма на комплексной плоскости комплексных амплитуд тока и напряжения на неидеальной индуктивности, здесь R - сопротивление индуктивности, X_L - реактивное сопротивление индуктивности, Z – полное комплексное сопротивление цепи.

Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90º. В цепи переменного тока напряжения на участках цепи складываются не арифметически, а геометрически. Если мы поделим стороны треугольника напряжений на величину комплексной амплитуды тока , то перейдем к треугольнику сопротивлений (рис. 4.3).

Рисунок 4.3. Треугольник сопротивлений для индуктивности L c реактивным сопротивлением X_L и с активным сопротивлением R. Здесь z - полное комплексное сопротивление цепи.

Из треугольника сопротивлений следует, что:

(4.7)

Если к конденсатору емкостью C подключить синусоидальное напряжение , то в цепи протекает синусоидальный ток:

(4.8)

Из анализа выражений (4.8) следует, что ток опережает напряжение по фазе на 90º. Выражение (4.8) в комплексной форме записи имеет вид:

(4.9)

где - емкостное сопротивление. А комплексное сопротивление идеальной емкости

На рис. 4.4 изображена векторная диаграмма цепи с емкостью

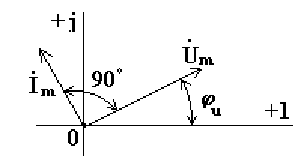
Рисунок 4.4. Векторная диаграмма комплексных амплитуд тока и напряжения на емкости.

Вектор тока опережает вектор напряжения на 90º.

Главное в главе 4

На сопротивлении переменный ток совпадает по фазе с напряжением, на емкости напряжение опережает ток на 90º, на емкости ток опережает напряжение на90º. Комплексные сопротивления: - активное сопротивление, - емкостное сопротивление, - индуктивное сопротивление.