3. Потенциал. Эквипотенциальные поверхности

Следует помнить, что работа по перемещению заряда q_пр в поле точечного заряда q из точки 1 в точку 2 не зависит от формы пути, а определяется только начальным и конечным положением зарядов (рис. 5).

Элементарная работа определяется по формуле:

Работа на всем пути:

и зависит только от расстояний r₁ и r₂. Следовательно, это поле является потенциальным и работа А_1→2 равна изменению потенциальной энергии

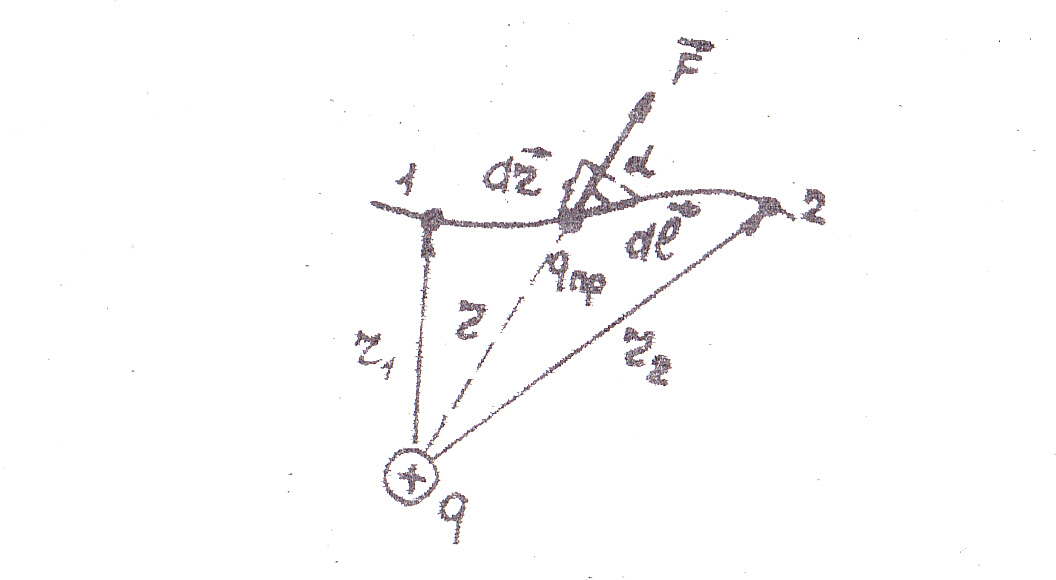
Рис. 5. Схема для вычисления работы

по перемещению заряда q_пр в поле заряда q

Потенциальная энергия взаимодействия зарядов q и q_пр равна

Отношение

(3)

является энергетической характеристикой поля, называемой потенциалом.

Потенциал — скалярная физическая величина, измеряемая отношением потенциальной энергии пробного заряда, помещенного в данную точку поля, к величине этого заряда.

Можно определить потенциал и через работу поля: потенциал данной точки поля равен работе, совершаемой полем при перемещении единичного положительного заряда из этой точки поля в бесконечность

Пример: Поле точечного заряда.

Потенциал поля точечного заряда q имеет следующий вид

. (4)

График функции φ(r) для точечного заряда представлен на рис. 6.

Рис. 6. График зависимости потенциала поля

точечного заряда от расстояния до точки наблюдения

Потенциал в СИ измеряется в вольтах

1 В = .

Знак потенциальной энергии взаимодействия зарядов q₁ и q₂ зависит от знака зарядов q₁ и q₂ : если заряды одноименны, энергии положительна (заряды отталкиваются), если заряды разноименны, энергия W — отрицательна (заряды притягиваются).

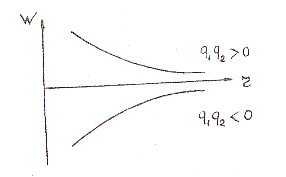
Рис.7. Потенциальная энергия

взаимодействия зарядов q₁ и q₂

Если заряд q перемещается в электростатическом поле из точки с потенциалом φ₁ в точку с потенциалом φ₂, то силы поля совершают работу

А = q(φ₁ — φ₂). (5)

Если поле образовано системой зарядов, то потенциал φ равен алгебраической сумме потенциалов полей, создаваемых каждым из зарядов в отдельности

.

Электростатическое поле можно изображать не только силовыми линиями, но и эквипотенциальными поверхностями — поверхностями рваного потенциала (рис. 8)

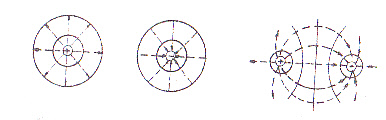
Рис. 8. Графическое изображение полей

силовыми линиями и эквипотенциальными поверхностями:

а) поле положительного заряда; б) поле отрицательного заряда:

в) поле диполя

Эквипотенциальные поверхности перпендикулярны линиям напряженности.

Задание 1. Заряд q' перемещается по пути 1→2→3→4→1 в поле заряда q. Определить величину работы на всем пути и на отдельных участках.

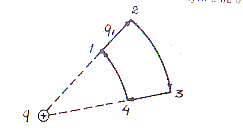
Задание 2. Определить потенциал поля в точке А.

Контрольные вопросы

1. В каких единицах измеряется потенциал электростатического поля?

2. Что означает утверждение: «электростатическое поле потенциала»?

3. Чему равна работа поля по перемещению заряда по замкнутому контуру?

4. Связь между напряженностью электрического поля и потенциалом

Векторная характеристика поля — напряженность связано со скалярной характеристикой поля потенциалом φ.

Эту связь можно проследить, рассматривая поле заряда q. Потенциал поля φ на расстоянии r от заряда будет составлять

;

на расстоянии r + dr

.

Эквипотенциальные поверхности достаточно близки (рис. 9)

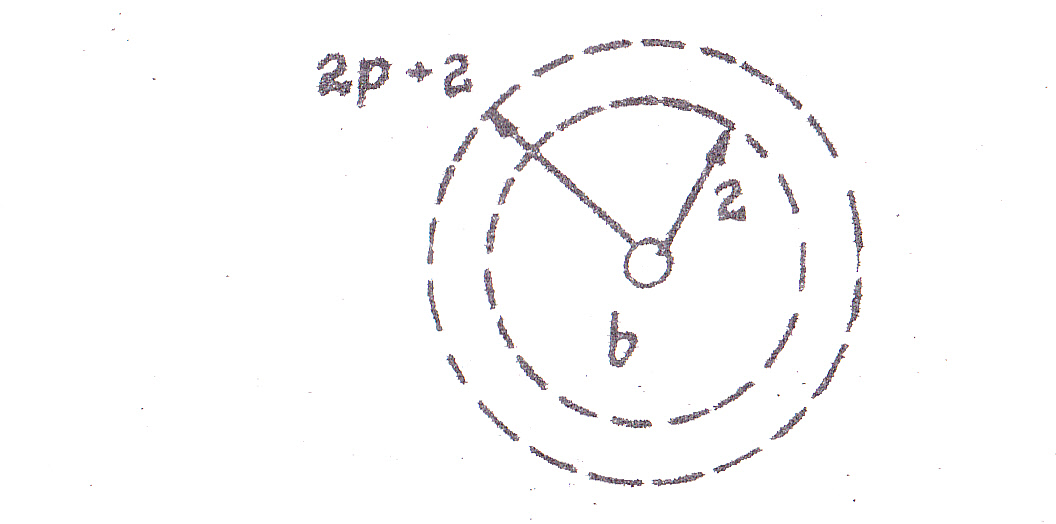
Рис. 9. Эквипотенциальные поверхности заряда q

на расстояниях r и r + dr

Найдем разность потенциалов: φ₂ — φ₁ = dφ

.

Поэтому

(6)

т. е. напряженность равна — производной от потенциала по расстоянию, взятому по направлению силовой линии. Формула (6) справедлива не только для поля точечного заряда, но и для любого электростатического поля. Ее иногда записывают в виде

Модуль напряженности поля, в данной точке определяется быстротой падения потенциала вдоль линии напряженности. Знак « — » показывает, что вектор направлен в сторону убывания потенциала.

Величина , характеризующая быстроту изменения потенциала в пространстве, носит название градиента потенциала

Е = — grad φ

Из формулы (6) видно, что напряженность электрического поля может быть выражена в вольтах на метр: [Е] = 1 В/м = 1 Н/Кл.

Задание 1. Известно, что потенциал поля между пластинами плоского конденсатора убывает согласно графику. Постройте график E (r).

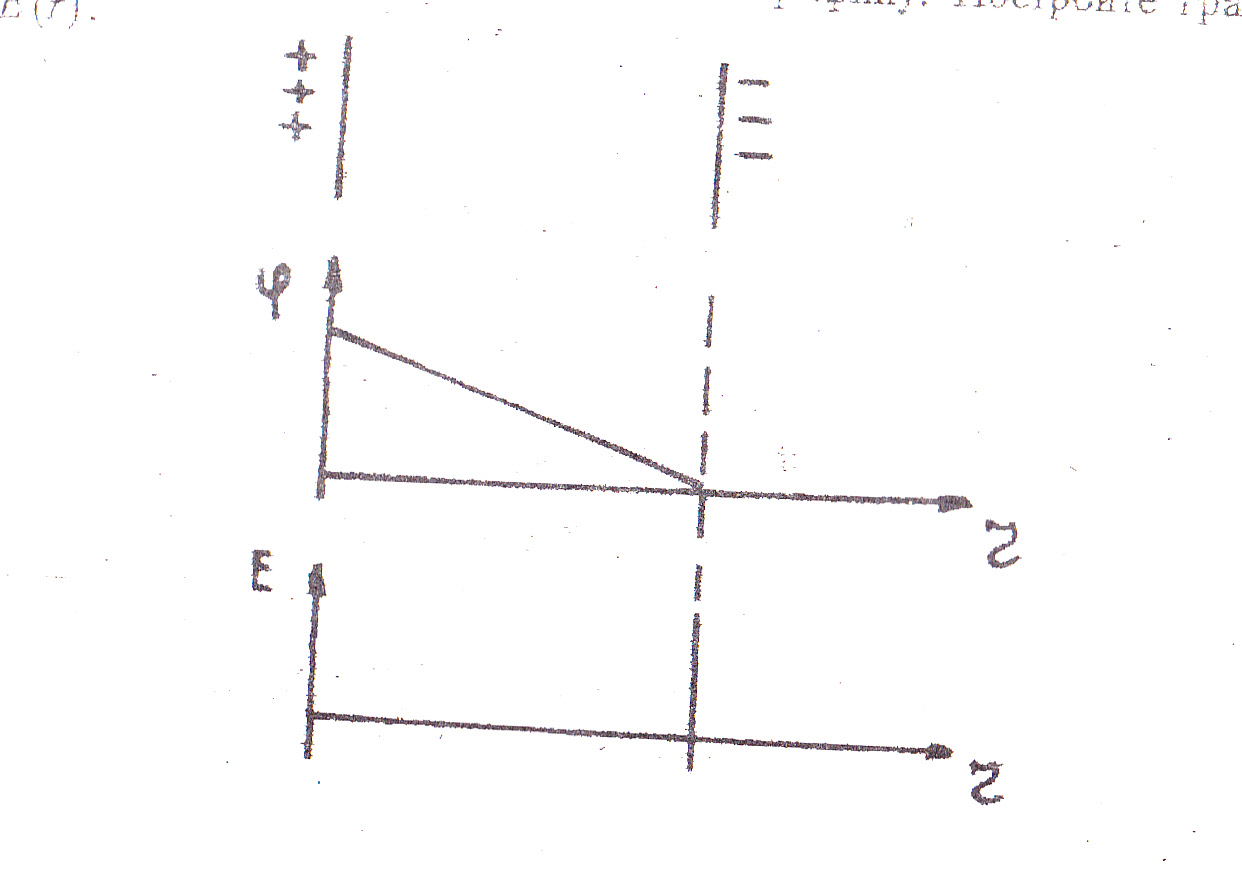
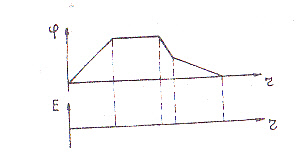
Задание 2. Дан график зависимости φ(r). Постройте график Е(r).

Контрольные вопросы:

1. В чем смысл знака «- » в формуле ?

2. Как, зная потенциал поля точечного заряда , можно найти напряженность этого поля?

3. В каких единицах можно измерять вектор напряженности?

ЗАНЯТИЕ № 2

Тема ДИПОЛЬ. ВЗАИМОДЕЙСТВИЕ ДИПОЛЬ — ДИПОЛЬ