Федеральное агентство по здравоохранению

и социальному развитию

САНКТ-ПЕТЕРБУРГСКАЯ ГОСУДАРСТВЕННАЯ

ХИМИКО-ФАРМАЦЕВТИЧЕСКАЯ АКАДЕМИЯ

Кафедра физики

Электростатика

Текст лекций

Санкт-Петербург

2006

УДК 537

Э45

Электростатика: Текст лекций/Сост. A.M. Скворцов, Е.М. Минаева, Т.И. Прокудина, Е.Д. Эйдельман. — СПб.: Изда-во СГГХФА, 2006.

28 с.

ISBN 5-8085-0170-9

Даны указания по изучению раздела электростатики курса «Физика и биофизика» в соответствии с учебной программой. Приведены примеры использования законов и контрольные вопросы.

Предназначены для студентов технологического фармацевтического факультета.

Под общей редакцией

докт. физ.-мат. наук, проф. Е.Д.Эйдельмана

Рекомендовано методической комиссией

фармацевтического факультета СПХФА

ISBN 5-8085-0170-9

Санкт-Петербургская государственная химико-фармацевтическая академия, 2006

ЗАНЯТИЕ № 1

Тема. ЗАКОН КУЛОНА, НАПРЯЖЕННОСТЬ, ПОТЕНЦИАЛ

1. Закон Кулона

Закон Кулона, установленный экспериментально с помощью кру­тильных весов в 1785 году, справедлив для точечных неподвижных зарядов. Точечными, так же как и тела в механике, считаются заряды, размерами которых можно пренебречь по сравнению с расстояниями между ними.

Пусть заряды q₁ и q₂ находятся на расстоянии r в вакууме. Тогда они будут взаимодействовать с силой , прямо пропорциональной величинам зарядов и обратно пропорциональной квадрату расстоя­ния между ними

F~ (1)

Кулоновские силы центральны, т. е. направлены по линии, соединяю­щей центры зарядов.

Задание. Изобразите кулоновские силы для одноименных и разно­именных зарядов (рис. 1).

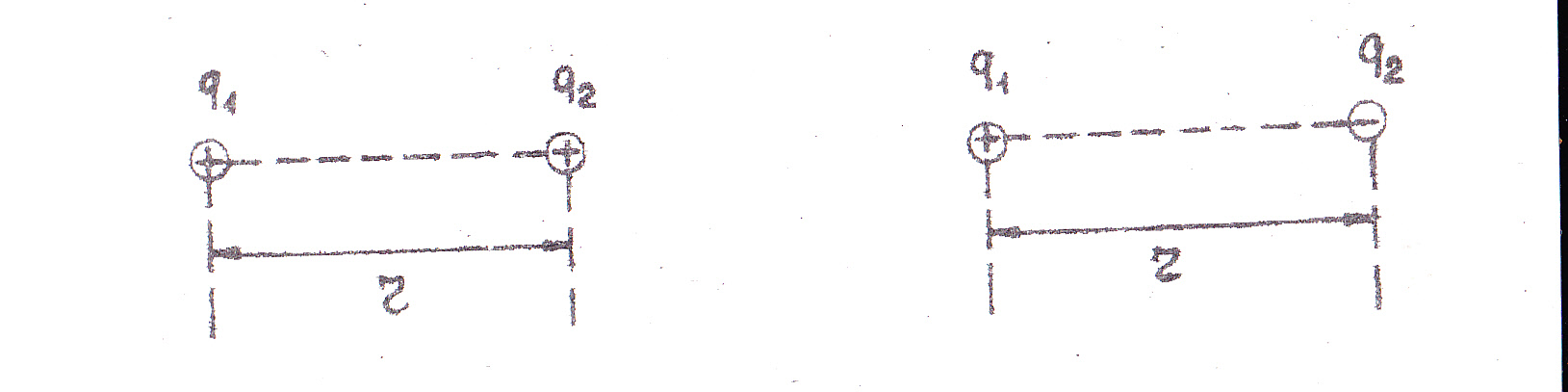
Рис. 1. Взаимодействие зарядов:

а) заряды имеют один знак;

б) заряды имеют, разный знак

Следует помнить, что при погружении зарядов в какую-либо среду, например, керосин или воду, сила взаимодействия уменьшится в ε раз (ε — диэлектрическая проницаемость среды; ε = 2 для керосина и ε = 81 для воды). В СИ формула (1) приобретает вид

где F измеряется в ньютонах, r — в метрах, величина зарядов q₁ и q₂- в Кулонах,

k = н·м²/Кл², а ε₀= 8.85·10^-12 Ф/м

Заряд электрона в СИ е = 1,6·10^-19 Кл.

Контрольные вопросы:

1. Расстояние между зарядами уменьшилось в 2 раза. Как и во сколько саз изменилась при этом сила взаимодействия зарядов?

2. Заряд q₁ увеличили в 2 раза. Как и во сколько раз изменилась кулоновская сила взаимодействия зарядов?

3. Как, не изменяя величин зарядов q₁ и q₂ и расстояния между ними r, можно уменьшить силу взаимодействия зарядов?

2. Напряженность. Силовые линии. Принцип суперпозиции электростатических полей

Всякий заряд q создает в окружающем его пространстве электростатическое поле. Обнаружить это поле в некоторой точке пространства можно, внося туда «пробный» заряд q_пр — малый точечный положительный заряд (этот заряд q_пр должен быть малым, чтобы не искажать поле заряда q).

На заряд q_пр, будет действовать сила

Отношение этой силы к величине пробного заряда не зависит от величины последнего и определяет поле заряда q

(2)

т.е. напряженность электростатического поля численно равна силе, действующей на единичный «пробный» положительный заряд, находящийся в данной точке поля.

Напряженность есть основная силовая (векторная) характеристика электрического поля. Знание напряженности позволяет найти величину силы, действующей на заряд в поле .

Пример 1: Поле :точечного заряда.

Из формулы (2) и закона Кулона следует, что напряженность поля точечного заряда равна

Графически зависимость Е(r) представлена на рис. 2.

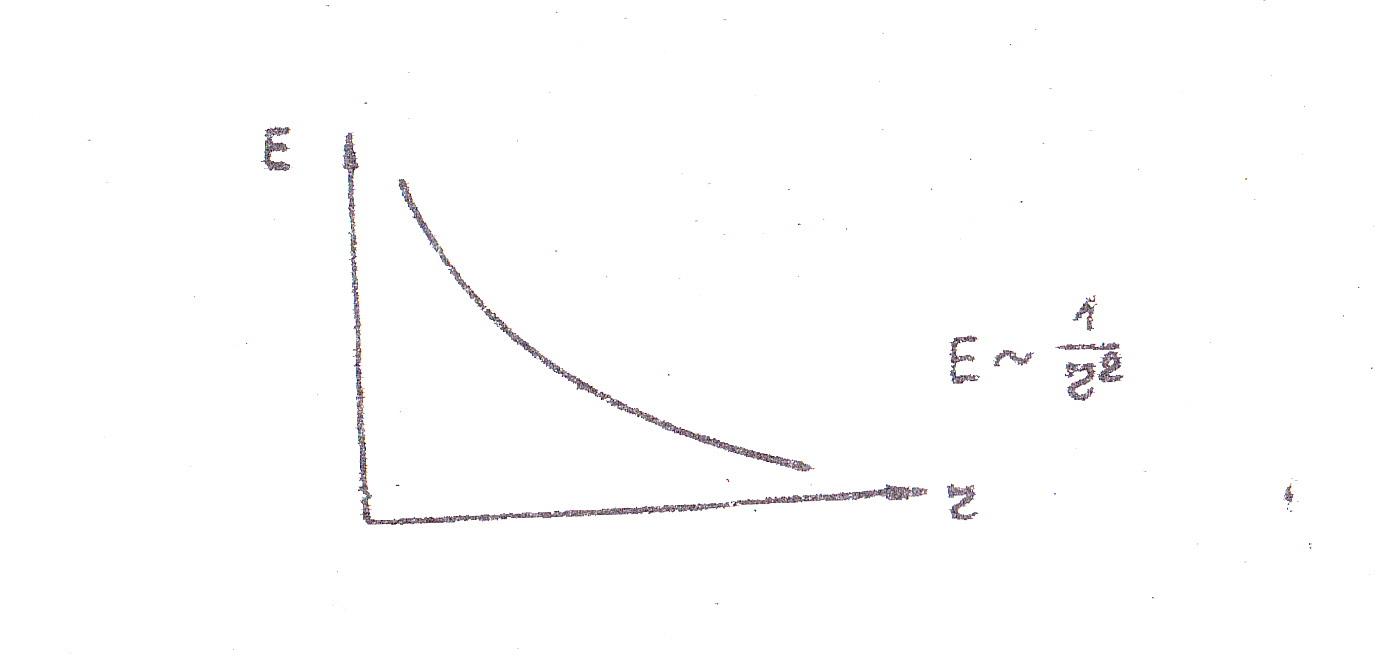
Рис. 2. Зависимость напряженности точечного заряда

от расстояния до точки наблюдения

Напряженность в СИ измеряется в Н/Кл или В/м

Поля внутри атома имеют порядок 10¹¹, Н/Кл; при грозах же возникают поля до 10⁶ Н/Кл.

Электрическое поле можно изобразить графически с помощью силовых линий — линий, касательные к которым в каждой точке поля совпадают с направлением вектора напряженности . Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности, перпендикулярной к линиям площадки, было равно численному значению напряженности. На рис. 3 графически изображены силовые линии электрических полей.

Линии напряженности могут начинаться или заканчиваться лишь на зарядах либо уходить в бесконечность, и не могут пересекаться.

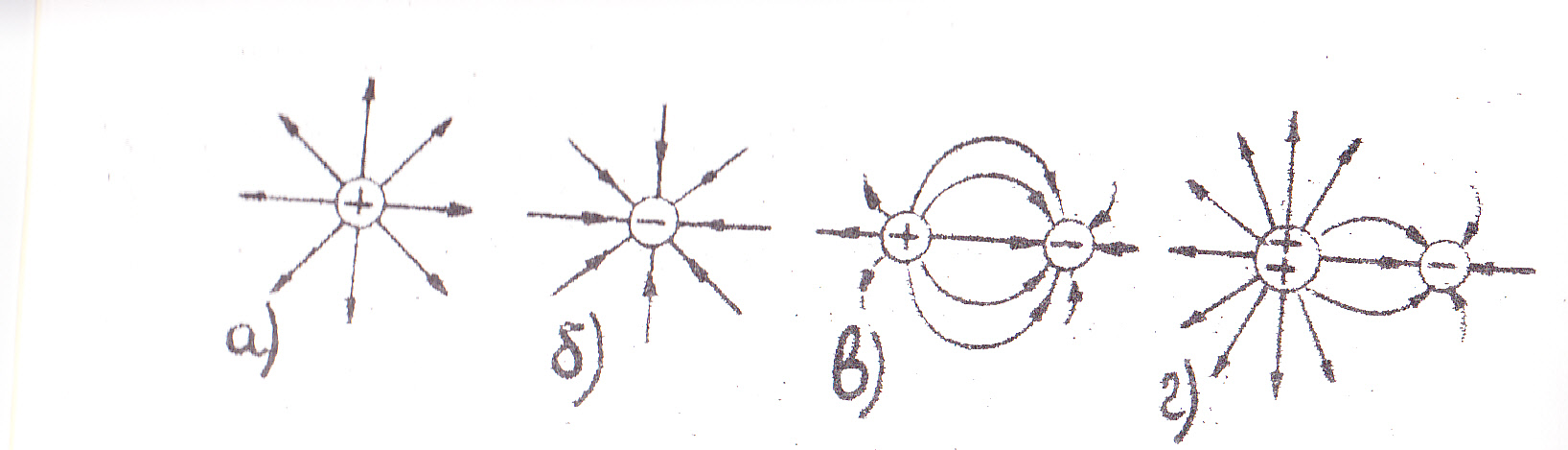
Рис. 3. Графическое изображение электростатических полей:

а) поле положительного заряда; б) поле отрицательного заряда;

в) поле диполя; г) поле двух зарядов +2q и –q.

Пример 2: Поле, созданное системой зарядов.

Известен принцип суперпозиции полей: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности.

Необходимо найти напряженность поля в точке А, если поле создается зарядами q₁ и q₂ (рис. 4),

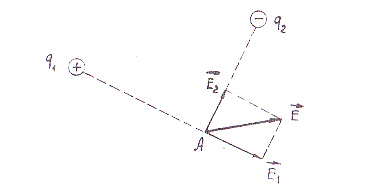
Рис. 4. Иллюстрация принципа

суперпозиции полей

Тогда нужно мысленно поместить в точку А «пробный» положительный заряд и посмотреть, какая сила действует на него со стороны зарядов q₁ и q₂ по отдельности; векторная сумма этих чисел дает искомую напряженность результирующего поля.

Задание 1. Найти- напряженность поля в точке А:

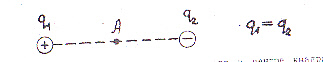
Задание 2. Найти напряженность поля в центре квадрата

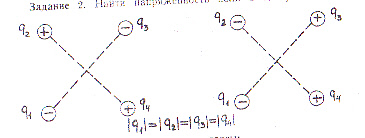
Контрольные вопросы:

1. В каких единицах измеряется вектор напряженности электростатического поля?

2. Почему силовые линии электростатического поля не пересекаются?

3. В чем состоит принцип суперпозиции полей?