Лабораторная работа № 5 статистическая обработка результатов измерений периода колебаний пружинного маятника

Любой эксперимент состоит из трех этапов подготовки, измерения, обработки. Результат измерений имеет малую ценность до тех пор, пока не указана его погрешность. Поэтому в задачу обработки экспериментальных данных входит не только нахождение измеряемой величины, но и оценка допущенной при измерениях погрешности. Повышение точности измерений плотности воды и азота, выделяемого из воздуха, привели в свое время к открытию дейтерия и аргона.

Погрешности повторных измерений одной и той же физической величины подчиняются статистическим закономерностям. С ростом числа измерений n погрешность среднего значения n результатов измерений убывает обратно пропорционально , а точность измерений растет.

В данной работе закон возрастания точности измерений с ростом их числа проверяется с помощью пружинного маятника (рис. 5.1), колебания которого моделируют, например, валентные колебания молекул.

Цель работы

Изучить закономерности статистической обработки результатов прямых измерений и показать, что погрешность среднего значения n результатов измерений убывает с ростом n обратно пропорционально .

Оборудование

1.Пружина, груз

2. Подставка для груза

3. Штатив

4. Секундомер

5. Линейка.

Теоретические сведения.

Рис. 5.1 Пружинный маятник.

1 — груз, 2 — подставка для груза, — пружина, 4 — штатив

Малые вертикальные колебания пружинного маятника (рис. 5.1).являются гармоническими. Это означает, что смещение груза из положения равновесия меняется со временем по закону синуса или косинуса. Гармонические колебания характеризуются амплитудой A и периодом T. Амплитуда — это размах колебаний, а период — это длительность одного полного колебания.

Период гармонических колебаний не зависит от амплитуды.

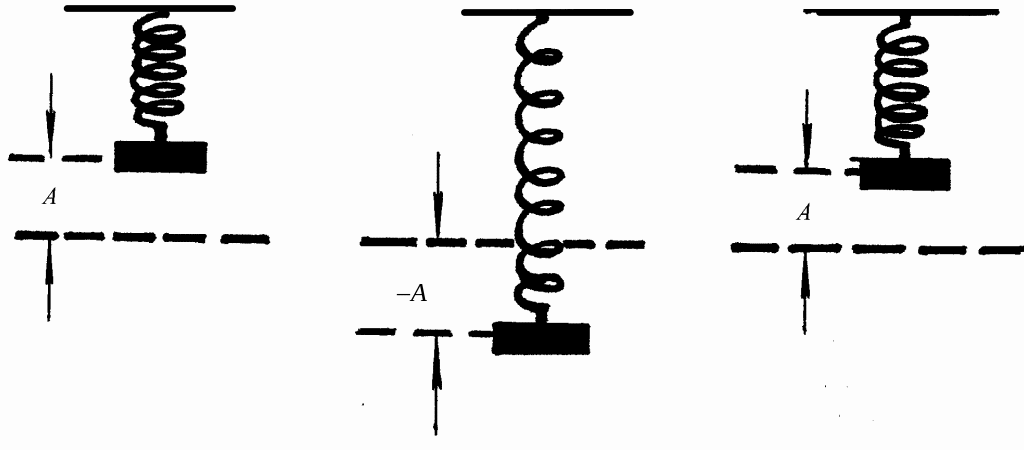
На рис. 5.2 показано положение груза при гармонических колебаниях с амплитудой А и периодом T в различные моменты времени на протяжении периода.

а) t = 0 б) в) t = T

Рис. 5.2. Положение груза на пружине при гармонических колебаниях с амплитудой A и периодом T в различные моменты времени на протяжении одного периода колебаний. Пунктиром показано положение равновесия

Период гармонических колебаний груза массы m на пружине жесткости k равен, как известно

. (1)

В положении равновесия сила тяжести груза уравновешена силой упругости, действующей на груз со стороны пружины mg = kx.

Здесь g — ускорение свободного падения, x = l  l₀ — абсолютное удлинение пружины, l — длина растянутой под действием груза пружины, l₀ — первоначальная длина нерастянутой пружины. Поскольку m/k=x/g, то период колебаний пружинного маятника может быть вычислен как

. (2)

Эта формула является расчетной. Измерив удлинение пружины x под действием груза, можно определить период колебаний T пружинного маятника. Размерность x] = м, размерность T] = с, величина g = 9,8 м/c².

Период колебаний, кроме того, может быть непосредственно измерен при помощи секундомера. Эти измерения относятся к прямым, поскольку числовое значение измеряемой величины отсчитывается непосредственно по шкале прибора. В работе измеряется длительность 20-ти полных колебаний груза на пружине. Значение T^(эксп.) рассчитывается по формуле.

T^(эксп.) = , (3)

где t — длительность 20 полных колебаний, индекс «эксп» означает экспериментальный.

Измерение длительности t и определение T^(эксп) производится n раз. В результате получается ряд величин T₁, T₂, ... T_n. Здесь символ T₁ означает результат первого измерения, т. е. значение периода, полученное при первом измерении, T₂ — результат второго измерения,... T_n — результат n-го измерения.

В качестве среднего значения группы n результатов измерений T₁, T₂, ... T_n , берется среднее арифметическое

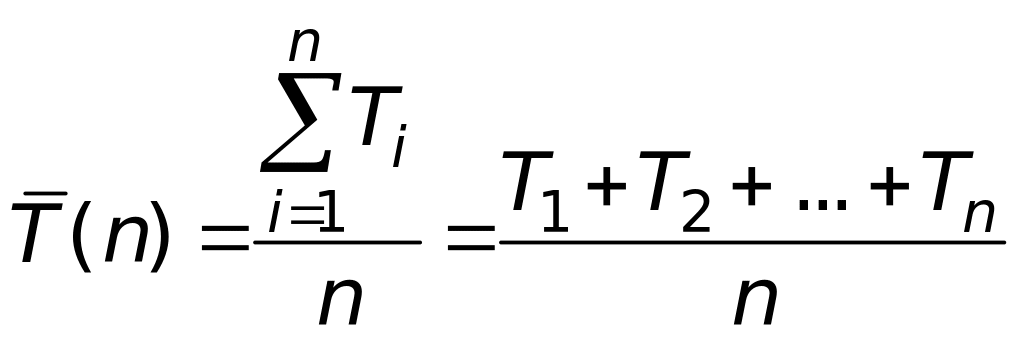. (4)

Символ означает среднее значение группы из n результатов измерений. Символ означает суммирование по i от i = 1 до i = n. Среднее значение является тем центром, вокруг которого разбросаны отдельные значения T_i. Мерой разброса этих значений вокруг среднего является абсолютная погрешность. Она тоже представляет собой некоторую среднюю величину. Но эта средняя величина вычисляется по более сложной формуле, чем среднее арифметическое.

Разность — отклонение результата первого измерения от среднего значения по n результатам измерений, далее, — отклонение результата второго измерения от среднего значения по n результатам измерений и т. д. вплоть до . Максимальное значение отклонения результатов измерений называется разбросом результатов и обозначается Т.

Вычислим сумму квадратов отклонений от среднего по формуле

(5)

Через s(n) обозначим среднее квадратичное отклонение среднего . Средним квадратичным отклонением среднего называется величина

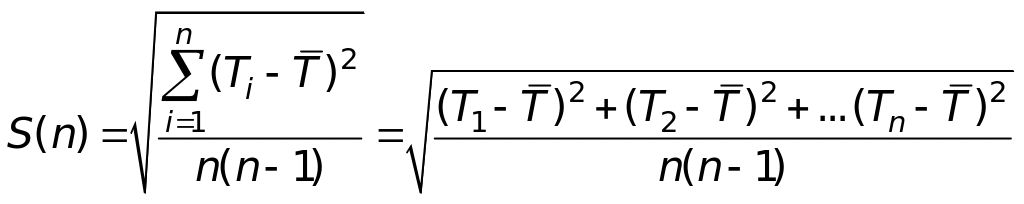, (6)

Предполагая, что отклонения подчиняются закону нормального распределения при доверительной вероятности 95% , нужно в качестве абсолютной погрешности взять удвоенное среднее квадратичное отклонение

T(n)= 2S(n) . (7)

Абсолютная погрешность  имеет такую же размерность, что и измеренная величина T. Абсолютная погрешность  характеризует погрешность того значения , которое получается в результате n произведенных измерений, а не какого-либо одного из них. Абсолютная погрешность  тем меньше, чем меньше разброс результатов T, и чем больше число измерений n.

Окончательный результат обработки записывают в виде

T =   (8)

или

–  < T < +  . (9)

Интервал значений от  –  до  +  называется доверительным интервалом.

В теории измерений доказано, что соотношения (8) и (9) имеют вероятностный смысл. Если T( )=2S( ), то точное значение T не может отличаться от среднего более чем на  c вероятностью 95%.

Наряду с абсолютной вычисляют относительную погрешность по формуле

(10)

Здесь E(n) означает относительную погрешность, выраженную в процентах. Относительная погрешность характеризует точность измерений.

С ростом числа измерений n абсолютная и относительная погрешности среднего убывают обратно пропорционально . Это утверждение проверяется в данной работе графически.

Из величин T₁, T₂, ... T₃₀ составляются шесть групп, содержащих результаты первых пяти измерений (T₁,T₂, ... T₅), первых десяти измерений (T₁, T₂, ... T₁₀), первых пятнадцати измерений (T₁, T₂, ... T₁₅), наконец, всех тридцати измерений (T₁, T₂, ... T₃₀). Каждая группа результатов T₁, T₂, ... T_n (n = 5, 10, ... 30) обрабатывается независимо от остальных.

В результате обработки экспериментальных данных T₁, T₂, ... T₃₀ по группам получается ряд средних значений T(5), T(10), ... T(30), ряд абсолютных погрешностей  (5),  (10), ...  (30), и ряд относительных погрешностей (5), (10), ... (30), отвечающих возрастающему числу измерений n. По этим данным строятся следующие графики. Во-первых, график зависимости среднего значения периода (n) от числа измерений n c указанием абсолютной погрешности  (рис. 5.4). Значения  откладываются вверх и вниз по вертикали от среднего значения (n). На том же графике (рис. 5.3) указывается теоретическое значение T_теор (пунктирная линия).

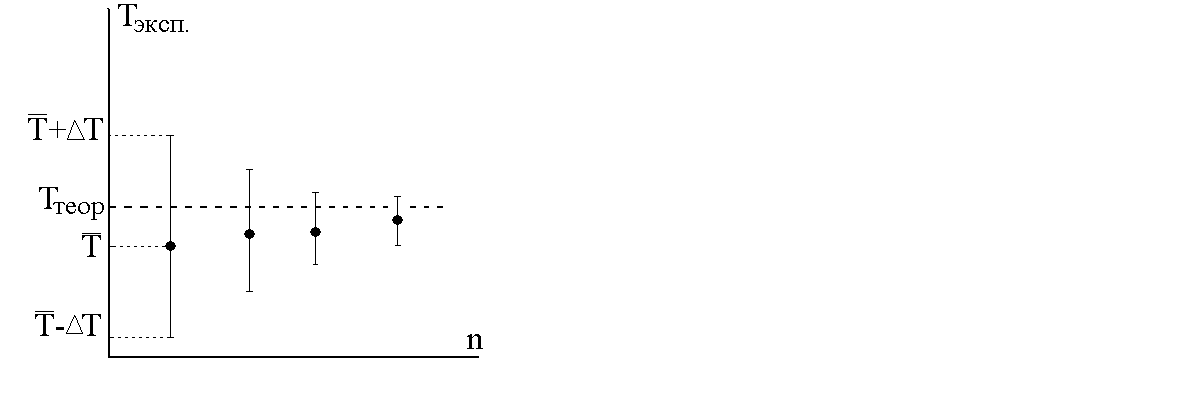Рис. 5.3. Теоретическое значение Т и «дорожка» экспериментальных значений, в зависимости от числа измерений n; Т- разброс результатов.

Теоретическое значение T рассчитывается по формуле (2). «Дорожка» экспериментальных значений отвечает границам доверительного интервала –  (нижняя кривая) и  +  (верхняя кривая). Наконец, строятся графики зависимости относительной погрешности E(n) от числа измерений n и относительной погрешности E(n) от (рис. 5.4)

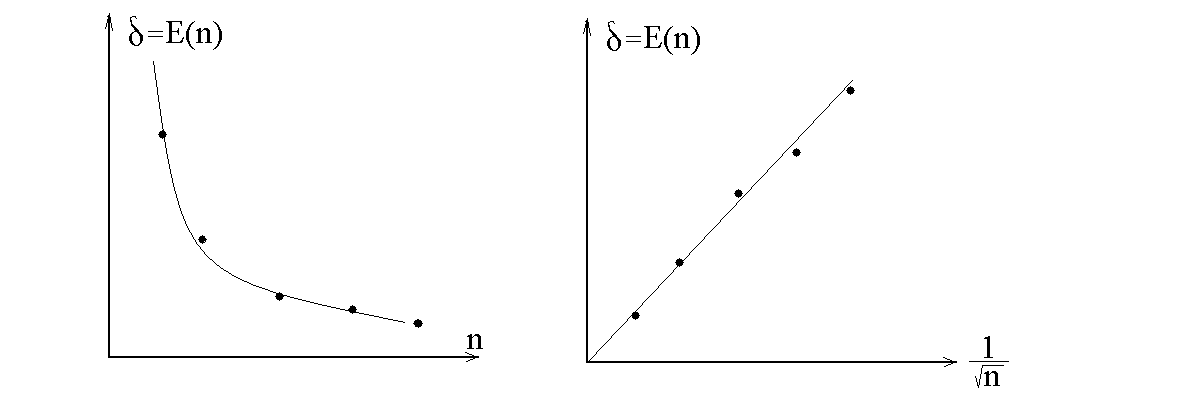
Рис. 5.4. Зависимость относительной погрешности E(n)= от числа измерений n и от обратного корня от числа измерений .

Поскольку относительная погрешность обратно пропорциональна , то график ее зависимости от 1/ должен представлять собой отрезок прямой линии.

Описание лабораторной установки

Пружинный маятник представляет собой груз 1, подвешенный на упругой пружине 3 (рис. 5.1). Масса пружины пренебрежимо мала по сравнению с 35ТО35сой груза. Груз представляет собой цилиндр с прорезью. Груз 1 ставится на подставку 2. Подставка 2 подвешивается к пружине 3. Пружина 3 подвешивается к штативу 4.

Порядок выполнения работы

1. Ознакомиться с лабораторной установкой.

2. Подвесьте пружину на штатив.

3. Измерьте первоначальную длину нерастянутой пружины l₀. Результаты запишите в табл. 5.1.

4. Поместите на подставку груз и подвесьте подставку с грузом на пружину.

5. Измерьте длину l растянутой под действием груза пружины. Результаты запишите в табл. 5.1.

6. Возбудите малые вертикальные колебания груза на пружине, сместив груз вверх из положения равновесия на 1 см и предоставив его самому себе. Определите длительность 20-ти полных колебаний t. Результат запишите в табл.5.2.

Внимание!

При измерениях следите за тем, чтобы колебания являлись вертикальными, а их размах был мал. Если колебания круговые, или вертикальные, но с большим размахом, прекратите измерение и начните опыт сначала.

7. Проделайте измерения длительности t 20-ти полных колебаний 30 раз, см. п. 6. Результаты запишите в табл.5.2.

8. Приведите лабораторную установку в порядок, снимите груз с подставкой с пружины, пружину — со штатива. Пружину положите в коробку.

Порядок обработки результатов измерений.

1. По данным табл.5.1 определите абсолютное удлинение пружины x (в метрах). Результаты запишите в табл.5.1

Таблица 5.1