Лабораторная работа № 3 изучение колебательного движения с помощью оборотного маятника

В курсе химии указывается, что молекула воды H₂O имеет уголковое строение, причем длина связи OH равна 0,097 нм, а валентный угол — 104,5°. Атомы в молекуле воды не находятся в покое, а совершают колебания. Имеются валентные колебания — это колебания атомов вдоль линий связи.

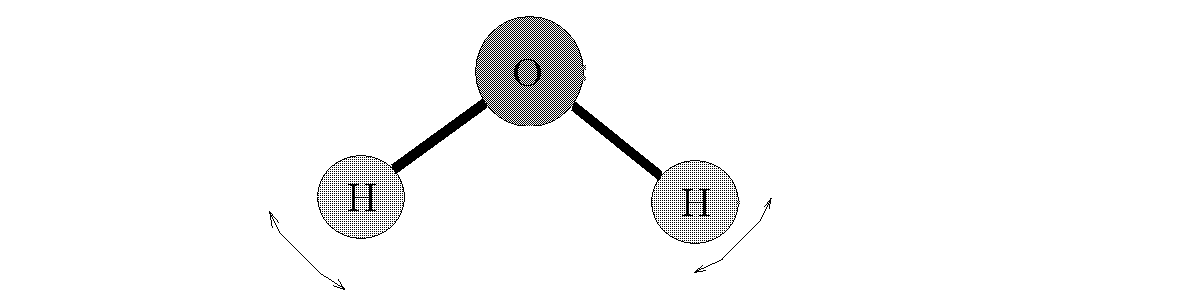
Рис. 3.1. Деформационные колебания атомов в молекуле H₂O

Но возможны и деформационные колебания, при которых изменяются углы между химическими связями, т. е. валентные углы (рис. 3.1). Если зафиксировать одну связь O—H, то колебания другой связи будет напоминать движение тела на нити, т. е. математического маятника. Итак, деформационные колебания моделируются колебаниями математического маятника.

Математический маятник является частным случаем более сложного оборотного маятника.

Для изучения закономерностей сложных колебаний в молекуле полезно познакомиться с моделью оборотного маятника и проделать данную лабораторную работу.

Цель работы

Изучить колебательное движение на примере оборотного маятника. Построить зависимость отношения периодов колебаний маятников Т/Т₀ от y по данным опыта и расчета, где T — период колебаний оборотного маятника, T₀ — период колебаний математического маятника, y = l/x— указаны на рис. 3.2.

Оборудование

1. Установки «Оборотный маятник» №1 (стержень деревянный) и №2 (стержень стальной).

Внимание! Определите, на какой установке Вы выполняете работу.

2. Секундомер.

3. Линейка.

Основные сведения

Оборотный маятник — система двух точечных грузов одинаковой массы m, находящихся на стержне по разные стороны от оси вращения. Масса стержня не учитывается (см. рис. 3.2.).

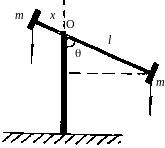
Рис. 3.2. Схема оборотного маятника, отклоненного на угол  от положения равновесия

Оборотный маятник совершает вращательное движение вокруг оси О. Основное уравнение динамики вращательного движения имеет вид

(1)

где  = d²/dt² угловое ускорение маятника,  - угол отклонения, который меняется с течением времени t.

Результирующий момент сил, действующих на оборотный маятник, вычисляется как

, (2)

где l и x длины нижней и верхней частей маятника (см.рис.3.2)

Момент инерции оборотного маятника, без учета массы стержня, равен

, (3)

Подставив результирующий момент сил и момент инерции в основное уравнение динамики вращательного движения, можно получить

(4)

При малых углах  можно считать, что sin   , и записать это уравнение в виде

(5)

где      (6)

и обозначено

Дифференциальное уравнение (5) соответствует гармоническим колебаниям с частотой и периодом

(7)

Так как

(8)

— период колебаний математического маятника, состоящего только из верхнего груза, то подставляя (8) и (6) в уравнение (4), получим

, (9)

.

Формула (9) является расчетной.

При больших значениях y, формула (9) упрощается, так можно приближенно считать, что 1+y²y², а y-1y. Тогда при y >>1

. (10)

Описание установки

Схема установки приведена на рис. 3.2. Она состоит из штатива со стержнем, к которому прикрепляются два груза одинаковой массы.

Порядок выполнения работы

Проведем сначала вычисления и заполним таблицу расчетов (табл. 3.1).

Таблица 3.1

Для 1-ой установки

№ п/п	x, м	l, м	y = l/x	1 + y2	y  1
1 2  10	0,1	0,1	1	2	0	

Таблица 3.1

Для 2-ой установки

№ п/п	x, м	l, м	y = l/x	1 + y2	y  1
1 2  10	0,04	0,04	1	2	0	

Данные для l возьмите на установке, располагая точки от l = x = 0,1 м до конца стержня равномерно.

Проверяем теперь эксперимент для данных значений x и l. Для чего:

1. Расположите верхний груз на расстоянии x = 10 см от оси вращения для 1-ой установки и на расстоянии x = 4см для 2-ой установки.

2. Нижний груз поместите в точку l = 10 см от оси вращения для 1-ой установки, для 2-ой установки l = 4 см

3. Отклонить стержень с грузом на угол ~10° и привести его в колебательное движение. Зафиксировать время 10 полных колебаний (движение «туда и назад»).

4. Данные занести в таблицу 3.2 результатов измерений и вычислений.

5. Каждый опыт проделать 3 раза.

6. Изменить расстояние l и проделать опыт снова. В таблице 3.2 брать только те значения l, для которых проделаны вычисления в таблице 3.1. Изменить расстояние l в 1-ой установке на 10 см, а во второй на 4 см.

Таблица 3.2

Для 1-ой установки

№ опыта	x, м	T0, с	l,м	t, c			tср c	n	T=tср/n, c	T/T0
				1	2	3
1	0,1		0,1
…
8

Таблица 3.2

Для 2-ой установки

№ опыта	x, м	T0, с	l,м	t, c			tср c	n	T=tср/n, c	T/T0
				1	2	3
1	0,04		0,04
…
10

Обработка результатов измерений.

1. Найдите среднее время 10 колебаний по формуле и период (n = 10).

2. Вычислите экспериментальное значение отношения периодов T/T₀ (T₀ находится по формуле (8)).

3. По данным таблиц построить (см.п.1.3 из Общих рекомендаций) на одной масштабной сетке графики T/T₀ = f(y) для расчетных и экспериментальных значений. Объяснить причины возможных отклонений.

4. По данным таблиц построить на одной масштабной сетке графики T/T₀ = f( ) для расчетных и экспериментальных значений. В выводах обратите внимание на форму зависимости при больших значениях y.

Контрольные вопросы

1. От чего зависит период колебаний математического маятника? Как T меняется с изменением длины маятника? Постройте график.

2. Будут ли отличаться периоды колебаний двух одинаковых математических маятников на Земле и на Луне?

3. Совпадают ли экспериментальные и расчетные графики в Вашей работе? В чем причина возможных отклонений?

4. Как изменится период колебаний математического маятника, если массу груза увеличить в два раза?