Лабораторная работа № 2 определение периода свободных колебаний груза на пружине
Одной из задач химии и биологии является изучение поведения молекул. Одним из важнейших явлений являются внутримолекулярные колебания. Например, в справочниках указано, что молекула водорода H2 имеет длину связи 0,075 нм, молекула HI – 0,162 нм, трехатомная молекула CO2 – 0,115 нм. Однако расстояния между атомами в молекуле не являются жестко фиксированными, а периодически изменяются в результате колебаний атомов вдоль линии связи. Такие колебания называются валентными (Рис.2.1). Если в линейной двухатомной молекуле зафиксировать положение одного атома, то в валентных колебаниях будет участвовать только второй атом. Закономерности таких валентных колебаний моделируются колебаниями пружинного маятника — груза, подвешенного на пружине.
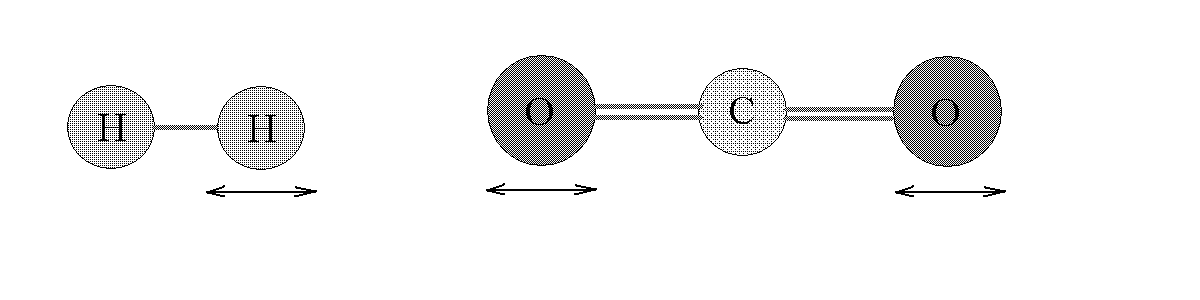
Рис. 2.1. Валентные колебания молекул H2 и CO2
Чтобы разобраться с колебательными процессами в молекулах, полезно познакомиться с гармоническим колебательным движением груза на пружине и выполнить данную лабораторную работу.
Цель работы
Установить зависимость периода свободных колебаний тела, подвешенного на пружине, от массы этого тела для пружин различной длины.
Оборудование
1. Штатив.
2. Линейка.
3. Три пружины различной длины.
4. Набор грузов различной массы (от 100 г до 500 г).
5. Секундомер.
Основные сведения
При упругой деформации пружины возникает сила, действующая на тело со стороны пружины и возвращающая его в положение равновесия. Эту силу обычно записывают в виде закона Гука.
F = k x, (1)
где F – проекция силы на ось x, x — величина деформации, т. е. смещение из положения равновесия, k — жесткость пружины.
Колебания, возникающие под действием упругой силы, являются гармоническими. Это значит, что зависимость смещения x от времени имеет вид
x = Acos(0 t), (2)
где A — амплитуда колебаний, 0 — циклическая частота собственных колебаний.
Известно, что циклическая частота собственных колебаний связана с характеристиками колеблющейся системы — жесткостью пружины k и массой тела на пружине m формулой
. (3)
Так как период колебаний (время одного полного колебания) связан с частотой
, (4)
то, подставляя (3) в (4), получаем
. (5)
Это соотношение проверяется в работе, то есть изучается зависимость периода свободных колебаний от массы груза, подвешенного к пружине.
Описание установки
Схема установки приведена на рис. 2.2. Она состоит из штатива, на котором закреплена пружина с чашечкой для подвешивания грузов.
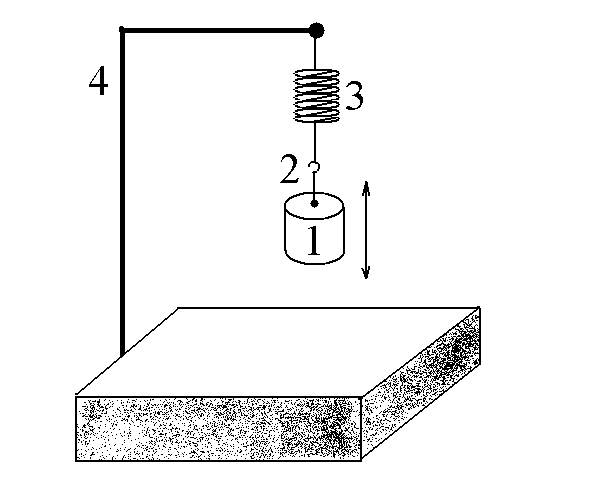
Рис. 2.2. Пружинный маятник:
1 — груз, 2 — подставка для груза, 3 — пружина, 4 — штатив
Период колебаний — минимальное время между двумя одинаковыми положениями груза на пружине (например, в нижней точке).
Порядок выполнения работы
1. Закрепить на штативе пружину с наименьшей длиной. Подвесить к ней чашечку для установки грузов.
2. Линейкой измерить длину недеформированной пружины l0.
3. На чашечку подвесить груз с наименьшей массой 100 г. Сам крючок весит 50 г. Общая масса груза составит 150 г.
4. Растянуть пружину на 1—2 см и заставить груз совершать малые вертикальные колебания. Определить время t 20-ти полных колебаний (n = 20).
5. Поместить на чашечку поочередно грузы 200 г, 300 г, 400г, 500 г. Учесть массу крючка 50г. Выполнить для них пункт 4.
Опыты проделать еще для 2-х пружин.
Обработка результатов измерений
Занести данные измерений и вычислений в табл. 2.1.
Таблица 2.1
-
№ пружины
l0, м
m, кг
t, с
n
Т, c
Т2, с2
1.
...
В таблице n — число колебаний тела на пружине.
2.
Период колебаний T
получается при делении времени колебаний
на их число, т. е.
.
3. По данным табл. 2.1 построить графики (см. п.1.3 из Общих рекомендаций) зависимости T от массы для трех пружин на одной масштабной сетке.
4. Построить графики зависимости T2 от массы также для трех пружин на одной масштабной сетке.
Контрольные вопросы
1. Чему равен период собственных колебаний тела, подвешенного к пружине?
2. От чего зависит период собственных колебаний тела на пружине?
3. Как по графикам зависимости T = f(m) и T2 = f(m) определить жесткость пружины? Как связана жесткость пружины с ее начальной длиной?
4. Как изменится период колебаний пружинного маятника, если увеличить длину пружины в четыре раза?
5. Будут ли отличаться периоды колебаний двух одинаковых пружинных маятников на Земле и на Луне?