1.4. Вычисления

Результат эксперимента, как правило,— некая числовая величина, поэтому провести до конца вычисления так же важно, как провести измерения. Способы борьбы с ошибками при вычислениях следующие.

Будьте аккуратны. Записывайте вычисления так, чтобы было много свободного места. Основная причина ошибок — неаккуратная и неразборчивая запись вычисления. При вычислении по сложной формуле составляйте таблицы. Например, вам надо вычислить.

,

при Q = 8. Сделайте таблицу.

A	B	C	D	E
x	(1 – x)2	x/64	B + C	D/8

Проверяйте вычисления. Для этого сначала нанесите их на график, тогда допущенная ошибка легко обнаружится, и вы увидите, что надо проверить (рис. 7).

При проверке старайтесь провести вычисления другим способом, например, в другой последовательности.

Рис. 7. Графическое обнаружение ошибок вычислений (точка р)

2. Рекомендации по обработке результатов измерений

2.1. Погрешности измерений

Измеряя какую-либо физическую величину x, мы не рассчитываем получить ее истинное значение x. Поэтому необходимо указывать погрешность измерения x, т. е. насколько полученный результат близок к истинному значению.

Допустим, мы проводим серию измерений некоторой величины x и после измерений получим значения x₁, x₂, x₃, ... x_n. В теории ошибок доказывается, что при отсутствии информации о причинах наблюдаемого разброса в качестве наилучшего значения искомой величины следует брать среднее арифметическое.

. (2.1)

Однако необходимо понимать, что одно и то же среднее значение может соответствовать сериям измерений имеющим различный разброс (сравните рис 8 а,б). Среднее арифметическое полученное по серии измерений б более «достоверно и надежно», чем по серии а. Чтобы избавиться от подобной неопределенности, любой честный экспериментатор должен указывать меру точности полученного среднего значения.

Итак,

(2.2)

Величина x называется абсолютной погрешностью и указывает пределы ошибки измерения.

Равенство (2.2) имеет вероятностный смысл. Мы можем с уверенностью сказать, что кто бы не проверял наши эксперименты, измеряемая величина практически почти всегда (обычно «почти» это 95 % случаев) будет находиться в пределах от до

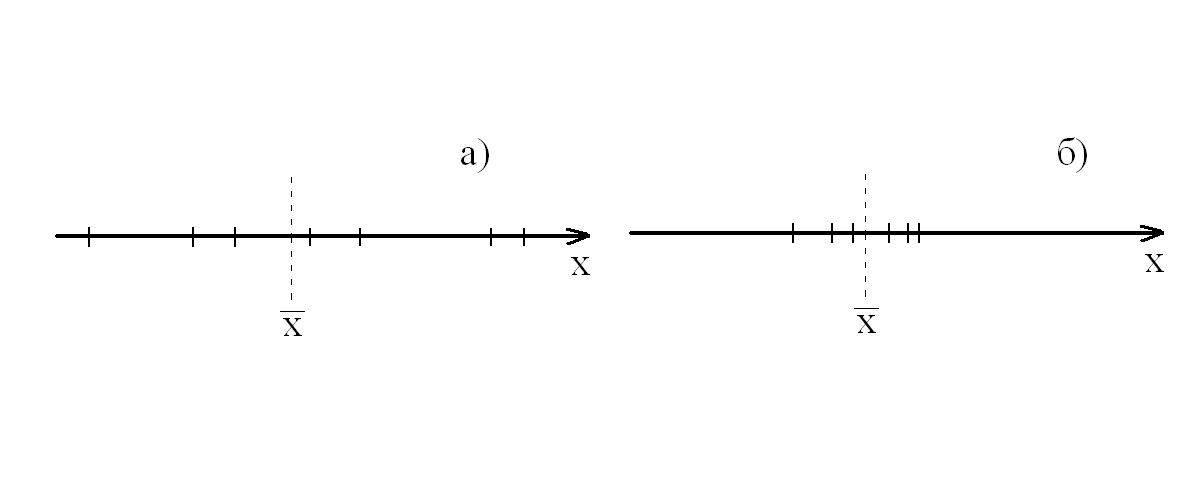
Рис. 8. Иллюстрация разброса результатов

серии измерений некоторой величины х.

Абсолютная погрешность x связана с величиной s, которая носит название средней квадратичной ошибки и вычисляется по формуле

(2.3)

Оказывается, что абсолютная погрешность измерений x = К_ss, где К_s коэффициент Стьюдента для вероятности 0,95 из таблицы.

Таблица 1

Число измерений n	Кs коэффициент Стьюдента для вероятности 0,95
2	12,7
3	4,3
4	3,2
5	2,8
7	2,4
10 и больше	2

Для характеристики точности измерений указывают также относительную погрешность (измеряется в %).

(2.4)

По способу получения результатов все измерения делятся на прямые и косвенные. В прямых измерениях искомое значение измеряемой величины находится непосредственно из отсчета по шкале прибора (например, измерение длины тела линейкой, времени — секундомером, силы тока — амперметром и т. д.). В косвенных измерениях результат определяется по формуле на основе прямых измерений других величин (например, определение скорости — по измерениям длины пройденного пути и промежутков времени).