Разделив равенства (3) и (2) почленно, получим

.

Зная ЭДС ₁ и отношение сопротивлений R_x /R, можно определить _х по формуле

(4)

Так как сопротивление проводника прямо пропорционально его длине, то отношение сопротивлений участков реохорда можно заменить отношением длин участка АВ, т. е.

,

Таким образом

(5)

Эта формула является расчетной.

Порядок выполнения работы

1. Собрать схему (рис. 33.2), включив в ветвь с гальванометром эталонный источник ₁ c ЭДС, равной 1,018 В. При сборке схемы особое внимание обратить на полярность подключения источников ЭДС.

2.Замкнуть ключ К₁ и К₂.

3. Перемещая подвижный контакт В, добиться отсутствия тока в ветви с гальванометром. Стрелка гальванометра должна показывать ноль.

4. Измерить длину участка АВ реохорда (l₁). Результат записать в табл.33.1.

5. Разомкнуть ключ К₂.

6. Включить исследуемый источник _х вместо эталонного источника ₁ Замкнуть ключ К₂.

8. Перемещая подвижной контакт В, добиться компенсации ЭДС _х по нулевому показателю гальванометра.

9. Измерить длину участка АВ (l_х). Результат записать в табл. 33.1.

10. Разомкнуть ключ К₂.

11.Опыт проделать (пункты с 1 по 10) десять раз при разных значениях ЭДС внешнего источника.

Таблица 33.1

Таблица измерений и вычислений параметров электрической цепи

Nп/п	l1 , см	lх , см	х , В	х-ср , В	(х- ср)2
1 2 3 … 10
			х ср=

Обработка результатов измерений

1. Рассчитать для каждого измерения l₁ и l_х по формуле (5) ЭДС источника _х. Результат занести в табл. 33.1.

2. Рассчитать абсолютную и относительную погрешность измерения. Действуйте в соответствии с «Порядком обработки результатов прямых измерений» (см.п.2.2. Общих рекомендаций). Для десяти измерений коэффициент Стьюдента K_S =2 Записать окончательный результат в виде

_х= _х  Δ_х

Контрольные вопросы

1. Из каких основных элементов состоит простая электрическая цепь?

2. Что составляет внутреннюю цепь, и какие элементы входят во внешнюю цепь?

3. Для какой цели предназначен источник ЭДС в электрических цепях?

4. Какие процессы происходят внутри источника?

5. Что называется электродвижущей силой?

6. Объясните принцип действия измерительной схемы компенсационного способа измерения ЭДС источника.

Лабораторная работа № 34 измерение сопротивлений методом моста постоянного тока

Цель работы

Изучить принцип действия и устройство измерительного моста постоянного тока

Оборудование

1. Источник питания

2. Магазин сопротивлений

3. Реохорд

4. Гальванометр

5. Измеряемые сопротивления –2 шт.

6. Ключ

Основные сведения

Одним из наиболее точных методов измерения сопротивлений является метод моста постоянного тока.

Принципиальная схема моста изображена на рис 34.1. Сопротивления R₁, R₂, R₃, R₄ называются плечами моста ветви АС и ВД диагоналями. В одну из диагоналей включается источник ЭДС  а в другую — гальванометр G.

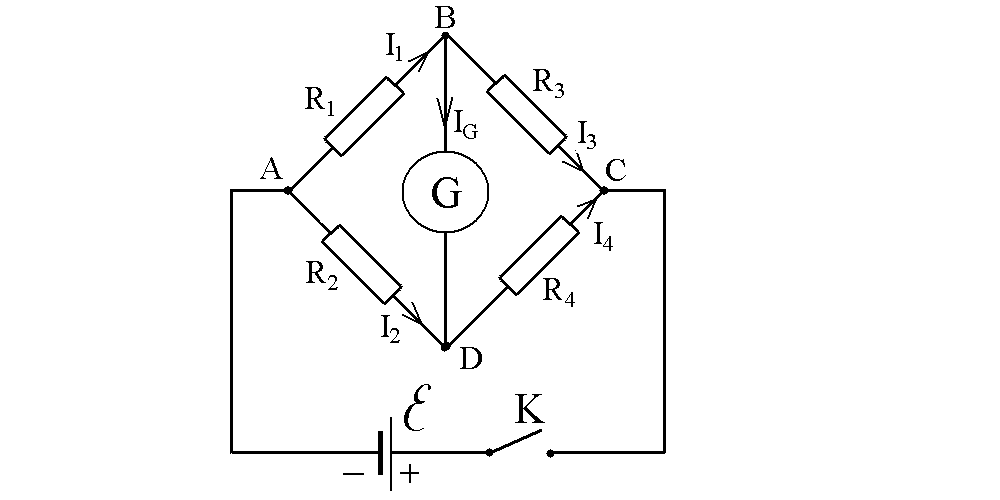
Рис. 34.1. Схема моста постоянного тока

С помощью моста постоянного тока можно определить сопротивление любого из четырех включенных в плечи моста. Процесс измерения сводится к тому, чтобы подобрать такие значения сопротивлений R₁, R₂, R₃, R₄, при которых ток в диагонали гальванометра был бы равен нулю. В этом случае напряжение на участке ВД будет отсутствовать, т. е. потенциалы точек _В и _Д будут равны друг другу. Такое состояние моста называется равновесным.

Так как ток I_G=0, то I₁= I₃ и I₂= I₄. Следовательно,

I₁ R₁= I₂ R₂; (1)

I₃ R₃= I₄ R₄. (2)

Поделив почленно эти равенства, получим

(3)

или

(4)

Пользуясь этим условием, можно определить любое из четырех сопротивлений, если известны остальные три сопротивления.

При измерении сопротивлений методом моста постоянного тока собирают цепь по схеме (рис. 34.2). В схеме R₂, R₄ — сопротивления участков реохорда (реохорд представляет собой укрепленную на линейке проволоку, вдоль которой перемещается скользящий контакт Д); R₁ = R_х, где R_х — неизвестное сопротивление; R₃ = R_м, где R_м — сопротивление магазина сопротивлений;  —ЭДС источника, G — гальванометр, К — ключ.

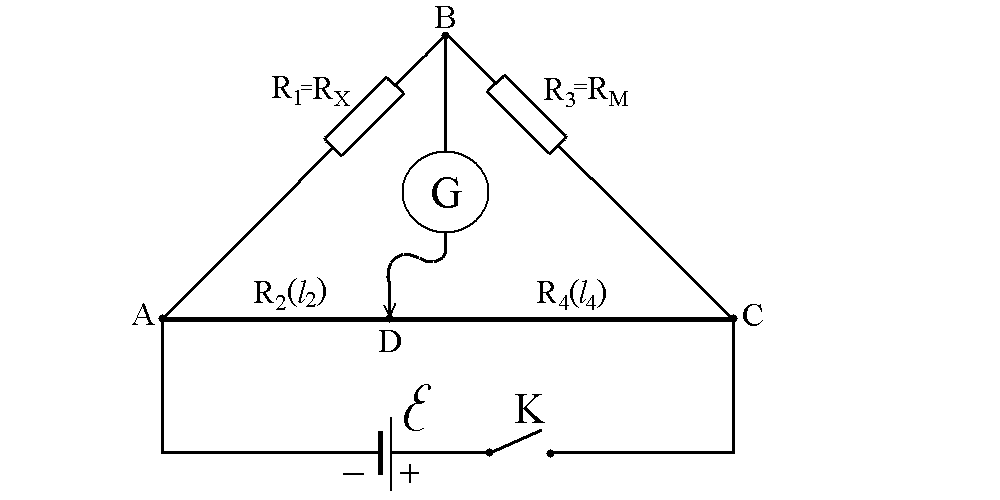
Рис. 34.2. Электрическая схема лабораторной установки

Монтажная схема моста постоянного тока лабораторной установки представлена на рис. 34.3.

Для участков реохорда АД и ДС можно написать, что

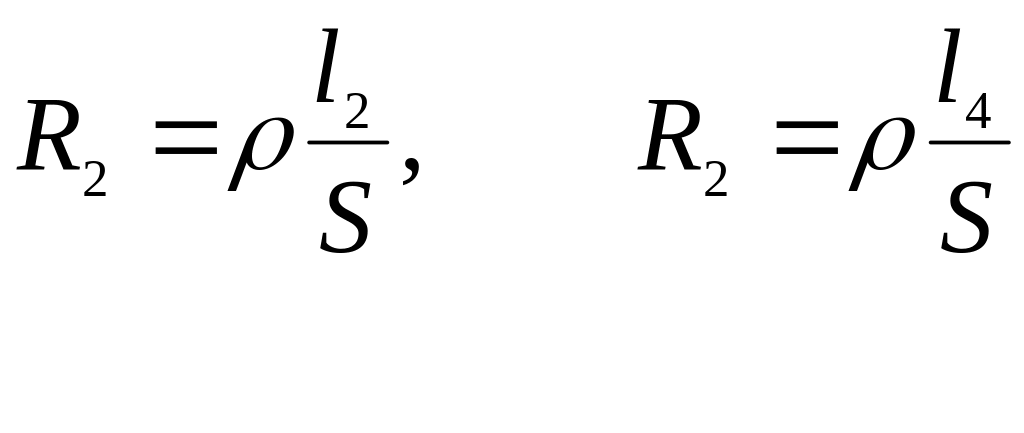(5)

где  — удельное сопротивление проволоки; S — поперечное сечение проволоки; l₂, l₄ — длины участков АД и СД.

В соответствии с этим равенство (4) принимает вид.

(6)

Если сопротивление R₁ = R_x, где R_x — искомое неизвестное сопротивление, а R₃ = R_м, где R_м – значение установленного сопротивления в магазине сопротивлений, то

. (7)

Эта формула является расчетной.

Порядок выполнения работы

1. Собрать цепь по схеме (рис. 34.3), включив в плечо R₁ неизвестное сопротивление R_x1.

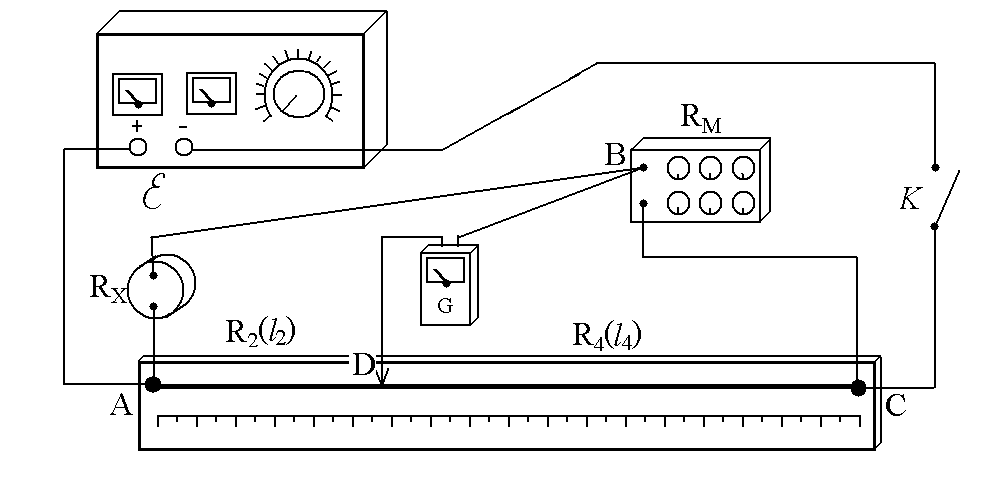
Рис. 34.3. Монтажная схема лабораторной установки

2. Установить подвижной контакт реохорда против деления 10 на горизонтальной шкале. Такое положение контакта Д будет соответствовать l₂ =10 см, l₄ = 40 см.

3. Замкнуть ключ К.

4. Подобрать в магазине сопротивлений такое значение сопротивления R_м, при котором стрелка гальванометра установится на ноль.

5. Значение сопротивления R_м занести в табл. 34.1.

6. Установить подвижной контакт реохорда против деления 20. Такое положение контакта Д будет соответствовать l₂ = 20 см, l₄ = 30 см.

7. Подобрать в магазине сопротивлений такое значение сопротивления R_м, при котором стрелка гальванометра установится на ноль.

8. Значение сопротивления R_м занести в табл. 34.1.

9. Проделать пункты 6, 7, 8 при положении контакта Д против значений l₂ указанных в табл. 34.1.

10. Разомкнуть ключ К.

11. Заменить сопротивление R_x1 на неизвестное сопротивление R_x2.

12. Замкнуть ключ К.

13. Измерить сопротивление R_x2 при положении подвижного контакта реохорда против деления 25. Результат измерения записать в отчет.

14. Разомкнуть ключ К.

Таблица 34.1

Таблица результатов определения сопротивления R_x1

N п/п	Rм ,Ом	l2 см	l4, см	Rх, Ом	Rх-Rxcp Ом	(Rх-Rxcp)2
1		10	40
2		20	30
3 4 5		25 30 10	25 20 40
---	--	--	--	Rх ср=
Rx2		25	25		--	--
Rx1,Rx2, соед.послед		25	25		--	--
Rx1,Rx2 соед.паралл		25	25		--	--

15. Соединить последовательно сопротивления R_x1 и R_x2.

16. Замкнуть ключ К.

17. Измерить последовательное соединение сопротивлений при положении подвижного контакта реохорда против деления 25. Результат измерения записать в отчет.

18. Разомкнуть ключ К.

19. Соединить параллельно сопротивления R_x1 и R_x2.

20. Замкнуть ключ К.

21. Измерить параллельное соединение сопротивлений при положении подвижного контакта реохорда против деления 25. Результат измерения записать в отчет.

22. Разобрать схему.

Обработка результатов измерения

1. При расчете сопротивлений пользуются формулой (7)

2. Проверить результат измерения последовательного соединения R_x1 и R_x2 по формуле

R_общ = R_x1 + R_x2.

3. Проверить результат измерения параллельного соединения R_x1 и R_x2 по формуле

4. Вычислить абсолютную и относительную погрешность измерения сопротивления R_x1.. Действуйте в соответствии с «Порядком обработки результатов прямых измерений» (см.п.2.2. Общих рекомендаций). Для пяти измерений коэффициент Стьюдента K_S =2,8 Окончательный результат записать в виде R_x1 = R_x1ср ± Δ R_x1.

Контрольные вопросы

1. От чего зависит сопротивление проводника?

2. Какие преимущества имеет мостовой метод измерения сопротивлений?

3. Как связаны между собой токи и напряжения в плечах равновесного моста?

4. Что измеряет гальванометр?

5. Могут ли сопротивления плеч равновесного моста быть равны друг другу?

6. Могут ли сопротивления плеч равновесного моста быть не равны друг другу?