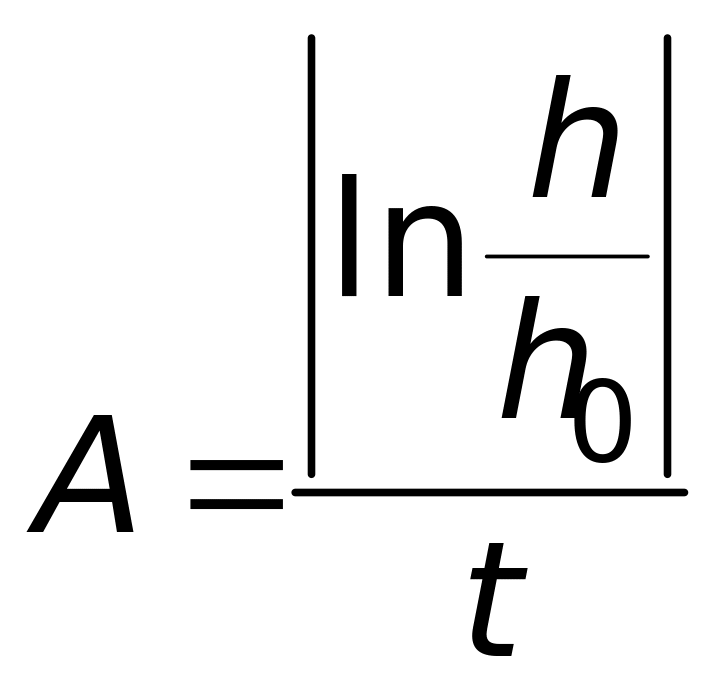Лабораторная работа №25 измерение коэффициента вязкости жидкости капиллярным методом

Цель работы

Научиться измерять коэффициент вязкости.

Оборудование

1.Лабораторный вискозиметр;

2. Секундомер;

3. Линейка.

Основные сведения

При движении слоев жидкости или газа относительно друг друга, между этими слоями возникают силы трения. Это явление называют внутренним трением. Свойство вещества проявлять внутреннее трение называют вязкостью. Количественной характеристикой вязкости каждого вещества является коэффициент вязкости . Величина коэффициента вязкости зависит от природы вещества, молярной массы и температуры. Для разных жидкостей и газов зависимости могут быть разными. Измерение коэффициента вязкости позволяет получить существенные сведения об изучаемом веществе.

При стационарном движении жидкости с постоянной скоростью, на неё действуют силы давления и силы вязкости (см. рис. 25.1.) Цилиндрические слои жидкости, соосные с осью трубы, смещаются друг относительно друга с различной скоростью. Слои прилегающие к стенкам будут иметь скорость стремящуюся к нулю. Быстрее всех будут двигаться слои ближайшие к центру. Силы вязкого трения, действующие на соседние слои определяются формулой Ньютона для вязкого трения.

, (1)

где S — площадь трущихся слоев, dv/dr — производная скорости движения по направлению, перпендикулярному к площади S.

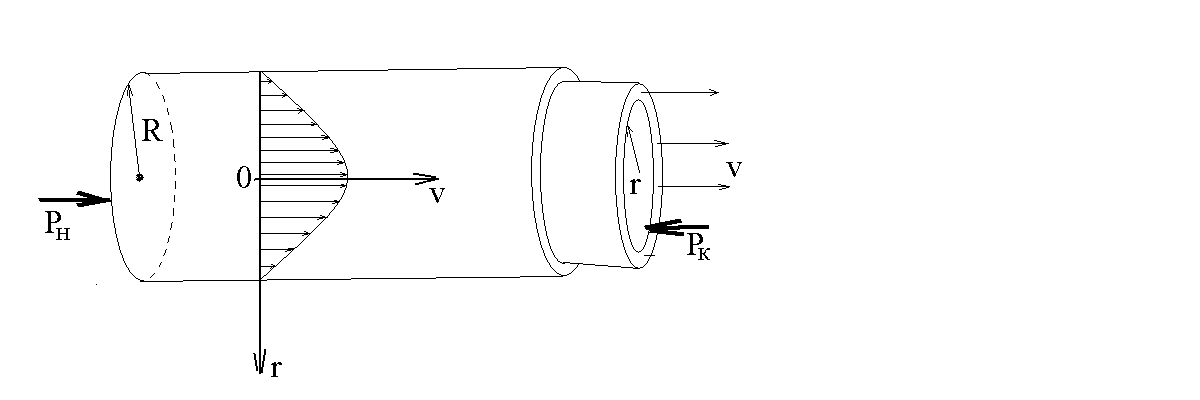
Рис. 25.1. Движение жидкости по трубе.

Если скорость движения мала, течение ламинарное (без завихрений), то расход жидкости текущей по цилиндрической трубе (капилляр это тоже труба, только очень тонкая) описывается формулой Пуазейля.

, (2)

где Q — расход жидкости или газа (м³/с), R — радиус трубы,  — коэффициент вязкости (Пас), р_н - р_к — разность давлений на концах трубы (Па), l -длина трубы.

Все величины, входящие в формулу (2) легко измерить. Метод измерения коэффициента вязкости, основанный на формуле Пуазейля, часто называют методом капилляра, а соответствующие приборы — капиллярными вискозиметрами. Тонкие капилляры используются потому, что в них легче всего обеспечить равномерное без завихрений течение жидкости.

Схема лабораторной установки приведена на рис. 25.2. Два сосуда одинакового сечения соединены гибкой трубкой. В трубки вставлен тонкий капилляр длиной l и радиусом R. Диаметр капилляра много меньше диаметра трубок, поэтому сопротивлением течению жидкости, оказываемым трубками можно пренебречь. Разность уровней жидкости в сосудах h создает перепад давлений на концах капилляра равный

р_н - р_к = gh (3)

где  — плотность жидкости, g — ускорение свободного падения.

Под действием этого перепада давления жидкость начинает перетекать через капилляр. Через малый промежуток времени dt разность уровней в сосудах изменится на величину dh. Объем жидкости, протекший за это время через капилляр равен

, (4)

где S — площадь поперечного сечения сосудов.

Если подставить равенства (3) и (4) в формулу Пуазейля, расход жидкости Q будет равен.

. (5)

Преобразуем (5) в дифференциальное уравнение

, (6)

где A - величина не зависящая от h или t.

Решением уравнения (6) является логарифмическая зависимость

, (7)

где h₀ — начальная разность уровней в момент времени t=0.

Сама величина h зависит от времени t по обратно-экспоненциальному закону .

График зависимости (7) будет прямой линией (см. рис. 25.3.) Тангенс угла наклона графика равен постоянной А.

. (8)

Коэффициент вязкости вычисляется по формуле

. (9)

Схема лабораторной установки

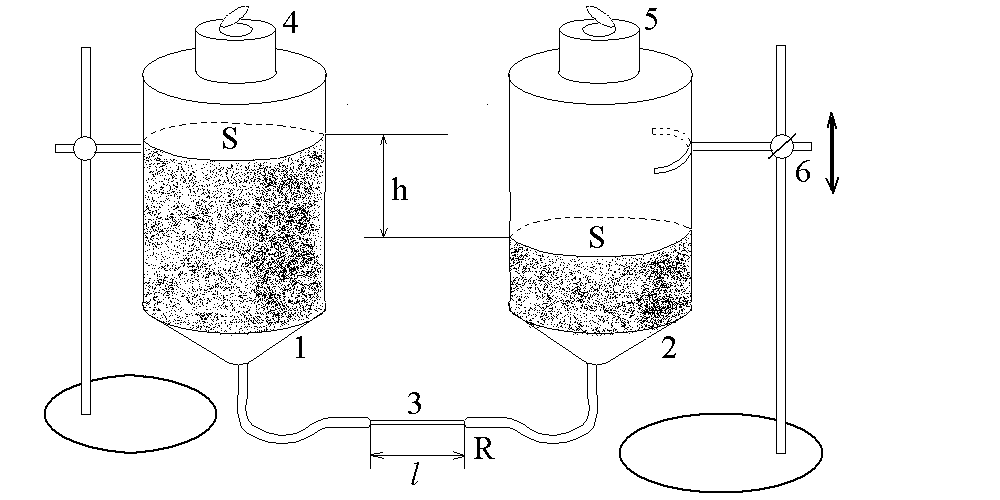
Рис. 25.2. Лабораторная установка для определения коэффициента вязкости жидкости капиллярным методом. 1 и 2 — сообщающиеся сосуды, 3 — капилляр, 4 и 5 — пробки, 6 — регулируемый штатив.

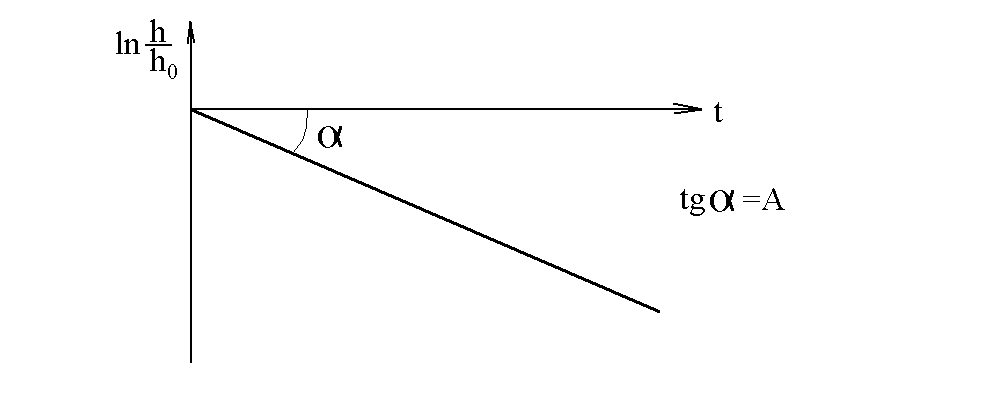
Рис. 25.3. График зависимости ln h/h₀ от времени.

Порядок выполнения работы

1. Закройте пробки на сообщающихся сосудах.

2. При помощи регулируемого штатива создайте начальную разность уровней между сосудами около h₀ =10 см.

3. Измерьте начальную разность уровней h₀ между сосудами.

4. Откройте пробки на сообщающихся сосудах.

5. Измерьте время, за которое разность уровней между сосудами уменьшится на h=1 см.

6. Повторите пункты 1-5 для значений h=2,3,4,5,6,7,8,9,10 см.

7. Данные опытов занесите в табл. 1.

Таблица 1

№ п/п	h, см	h=h0-h, см	t, с			I, Пас	i-ср	(i-ср)2
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10	10

Обработка результатов измерений

1. Рассчитайте тангенсы угла наклона графика по формуле (8) и занесите в табл. 1.

2. Рассчитайте значения коэффициента вязкости по формуле (9) и занесите в табл.1. Значения , g, R, l, S указаны на установке.

3. Вычислите среднее значение коэффициента вязкости _ср.

4. Вычислите абсолютную погрешность . Действуйте в соответствии с «Порядком обработки результатов прямых измерений (п.2.2 в Общих рекомендациях). Для десяти измерений коэффициент Стьюдента K_S =2.

5. Постройте график (см. п.1.3. в Общих рекомендациях) зависимости lnh/h₀ от времени t.

6. Постройте график зависимости h от времени t.

7. Сделайте выводы из полученных результатов.

Контрольные вопросы

1. От чего зависит коэффициент вязкости?

2. Как зависит коэффициент вязкости от радиуса капилляра?

3. Как изменится расход жидкости, если радиус капилляра при прочих равных увеличится в два раза?

4. Как изменится график зависимости h от времени t, если увеличить коэффициент вязкости жидкости?

5. Запишите и поясните формулу Ньютона для силы вязкого трения.