Лабораторная работа № 24 определение отношения ср/cv методом клемана и дезорма
Цель работы
Определение отношения теплоемкости газа при постоянном давлении (ср) и теплоемкости при постоянном объеме (cv) для воздуха методом Клемана и Дезорма.
Оборудование
1. Стеклянный баллон;
2. U-образный манометр;
3. Насос,
4. Секундомер.
Основные сведения
Теплоемкость тела (или системы) — это количество теплоты Q, необходимое для нагревания этого тела на один (градус) кельвин, Cтела=Q/T. Теплоемкость тела измеряется в Дж/К.
Теплоемкость моля вещества, называемую молярной теплоемкостью, будем обозначать с.
Молярная теплоемкость — количество тепла, необходимое для нагревания одного моля вещества на один кельвин. Имеем
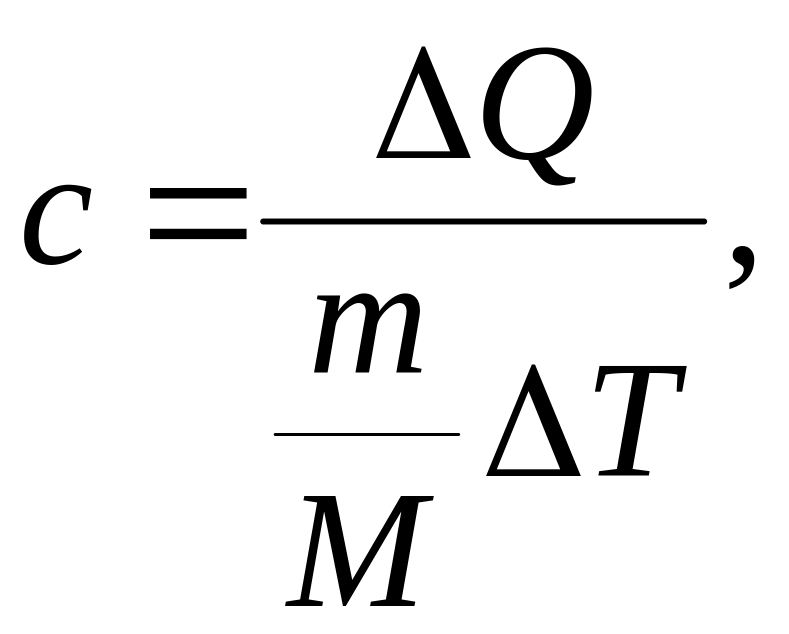(1)
где М — молярная масса вещества, m – масса вещества.
В СИ молярная теплоемкость измеряется в Дж/моль.К. Заметим, что эта размерность совпадет с размерностью универсальной газовой постоянной R.
Теплоемкость вещества зависит от условий, при которых происходит нагревание газа. Наибольший интерес представляет теплоемкость для случаев, когда нагревание происходит при постоянном объеме или при постоянном давлении. В первом случае теплоемкость называется теплоемкостью при постоянном объеме (сV), во втором — теплоемкостью при постоянном давлении (ср).
Классическая теория теплоемкости приводит к следующим значениям удельных и молярных теплоемкостей
(2)
,
(3)
где i — число степеней свободы.
Как видно из (2) и (3) сV и ср связаны между собой уравнением, ср- сV=R, которое называется уравнением Майера.
Отношение ср/ сV= входит в уравнение адиабатного процесса
рV = const (4)
или
(5)
называют показателем адиабаты или коэффициентом Пуассона, т. к. уравнение (4) называют уравнением Пуассона.
Отношение ср/ сV= = i+2/i зависит от числа степеней свободы i, а это число зависит от атомности газа. Запишем:
— для одноатомных газов i = 3, =5/3=1,67
— для двухатомных газов i = 5, =7/5=1,4
— для многоатомных газов i = 6, =8/6=1,33
Экспериментальная установка состоит из стеклянного баллона А, соединенного с манометром В и насосом (рис. 24.1).
Кран С позволяет сообщать баллон А с атмосферой.
Если при помощи насоса накачать в баллон некоторое количество воздуха, то давление и температура воздуха внутри баллона повысятся.
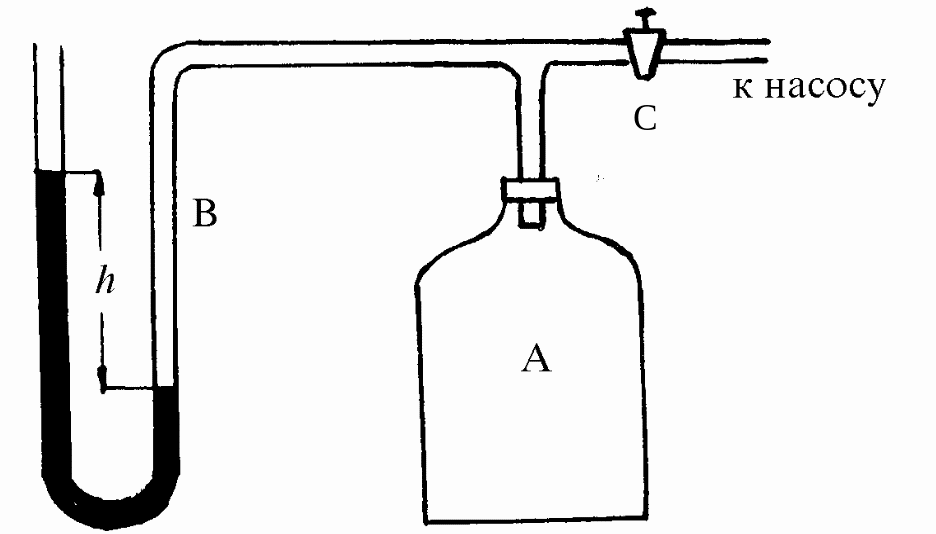
Рис. 24.1. Экспериментальная установка
Избыточное по сравнению с атмосферным давление воздуха в баллоне А измеряется U-образным манометром.
Через некоторое время воздух в сосуде охладится и его температура станет равной комнатной температуре T1.
Давление, установившееся в баллоне, будет р1 = H + h1, где H—атмосферное давление, h1 — добавочное давление, измеряемое разностью уровней жидкости в манометре.
Вынув на несколько долей секунды кран С из гнезда, заставляют часть воздуха выйти из сосуда, вследствие чего давление в сосуде уравновешивается с атмосферным H.
При расширении воздуха температура в сосуде А понизится до T2. Затем закрывают кран С. Через некоторое время воздух в сосуде А нагреется до температуры окружающего воздуха, сохранив свой объем неизменным. При этом увеличится давление до величины р2 = H + h2, где h2 — новая разность уровней в манометре.
Обозначим объем той массы воздуха, которая осталась в сосуде после удаления части ее (когда была открыта на несколько секунд пробка c) — V2. До открывания крана та же масса воздуха занимала (какой-то) меньший объем V1, так как кроме этой массы воздуха в сосуде А находилось еще некоторое количество воздуха, вышедшего при открывании крана С.
Таким образом, мы имеем 3 состояния воздуха, которые характеризуются следующими параметрами.
1. До открытия крана С V1; H+h1; T1.
2. В момент открытия крана V2; H; T2.
3. После закрытия крана
(когда установилась температура) V2; H+h2; T1.
Так как в первом и третьем состояниях воздух имел одну и ту же температуру, то применяя закон Бойля-Мариотта (р1V1=р2V2), получим
или
. (6)
Переход из одного состояния во второе происходит настолько быстро, что теплообмена за столь короткое время не произойдет. Этот процесс расширения можно считать адиабатным.
Применяя к первому и второму состоянию уравнение Пуассона (5), получим
или
.
(7)
Возведя обе части уравнения (6) в степень y
(8)
и, сопоставляя выражение (7) и (8), получим
(9)
Для удобства это выражение запишем так
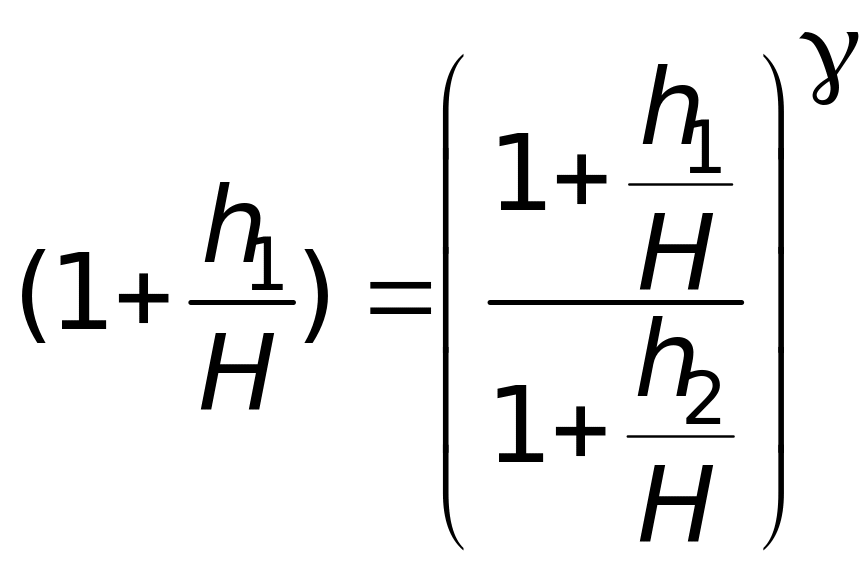. (10)
Логарифмируя выражение (10) и решая относительно , находим
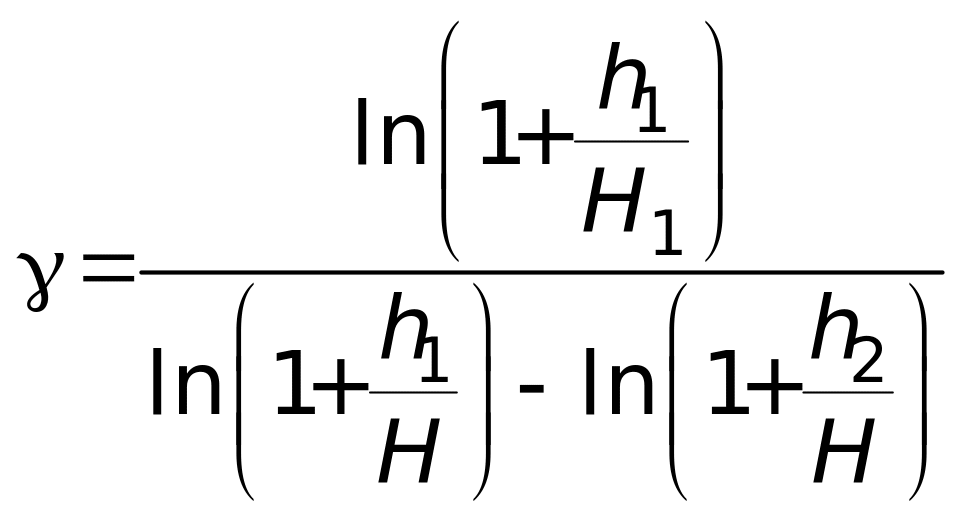. (11)
Так как h1/H <<1 и h2/H <<1 то ln(1+ h2/H )и ln(1+ h1/H ) можно разложить в ряд. Например,
. (12)
Если h1/H и h2/H мало, то можно в разложении (12) ограничиться лишь первым членом.
Тогда (11) принимает вид
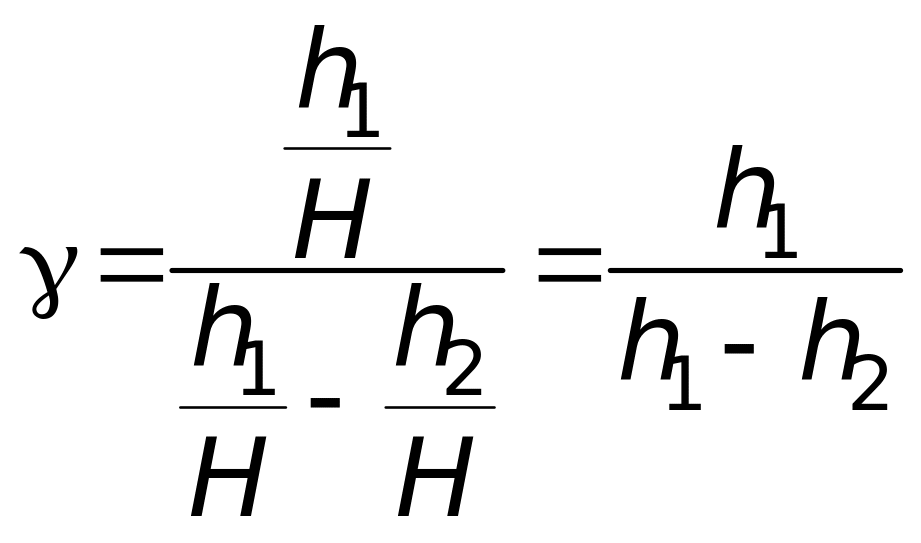. (13)
Таким образом, экспериментальное определение = cр/cV сводится к измерению h1 и h2.
Порядок выполнения работы и обработка результатов