Данные для построения графика ln(f(X)/X)

	U = x	U = x2	(x)	(x)/x	ln ((x)/x)
1 2 3 4 5

4. По данным табл. 20.2 постройте график ln ((x)/x) и сделайте выводы по проделанной Вами работе.

Контрольные вопросы

1. Как изменится график I/x = f(x) при увеличении (уменьшении) температуры катода?

2. О чем говорит линейность графика ln ((x)/x)?

3. Как изменится график ln ((x)/x) при увеличении (уменьшении) температуры катода?

4. Почему функции распределения Максвелла для идеального газа и электронного газа в вакуумном диоде отличаются?

5. Чему равна площадь под графиком I/x = f(x)?

Лабораторная работа № 21 определение коэффициента внутреннего трения жидкости методом стокса

Цель работы

Определение коэффициента внутреннего трения (вязкости) жидкости методом Стокса.

Оборудование

1. Цилиндр с вязкой жидкостью.

2. Шарики различных диаметров.

3. Микрометр.

4. Секундомер.

Основные сведения

В жидкости разные слои могут иметь различные скорости движения друг относительно друга (рис. 21.1).Так как молекулы жидкости вследствие теплового движения могут переходить из одного слоя в другой, перенося с собой количество движения (импульс), то со стороны слоя, движущегося с относительно большей скоростью, на слой, движущийся с меньшей скоростью, действует ускоряющая сила. Наоборот, со стороны слоя, движущегося медленно, на быстро движущийся слой действует задерживающая сила. Эти силы, называемые силами внутреннего трения, направлены по касательной к поверхности слоев.

На рис. 21.1 выделены пунктиром два слоя жидкости, отстоящие друг от друга на расстоянии z. Скорости слоев — v₁ и v₂ — соответственно, а разность их скоростей v = v₁ – v₂.

Величина dv/dz, показывающая, насколько быстро меняется скорость при переходе от слоя к слою (резкость изменения скорости), носит название производной скорости. Размерность производной скорости [1/c].

Рассмотрим выделенную площадку соприкасающихся слоев площадью S. Величина силы внутреннего трения F будет тем больше, чем больше рассматриваемая площадь S поверхности слоя и чем больше производная скорости.

. (1)

Формула (1) называется формулой Ньютона для силы вязкого трения. Ось oZ, вдоль которой вычисляется производная скорости, направлена перпендикулярно к площади S.

Величина , зависящая от природы жидкости, называется коэффициентом внутреннего трения или коэффициентом вязкости жидкости. Коэффициент вязкости жидкости численно равен силе, действующей на единицу площади соприкасающихся слоев, когда изменение скорости в перпендикулярном к слоям направлении равно 1 (v/z = 1). Коэффициент вязкости в СИ измеряется в Па·с.

Чем больше коэффициент вязкости, тем большие силы внутреннего трения в ней возникают. Вязкость жидкости существенно зависит от температуры; с повышением температуры коэффициент вязкости жидкости уменьшается. Так, например, вязкость воды при повышении температуры от 0 до 20 градусов уменьшается почти вдвое. В отличие от жидкости, коэффициент вязкости газов возрастает с ростом температуры по закону _газа ~ . Величины коэффициентов вязкости жидкостей и газов различаются на несколько порядков, например, при t = 20°C для воды  = 10^–3 Па·с, а для воздуха  = 1,7·10^–5 Па·с.

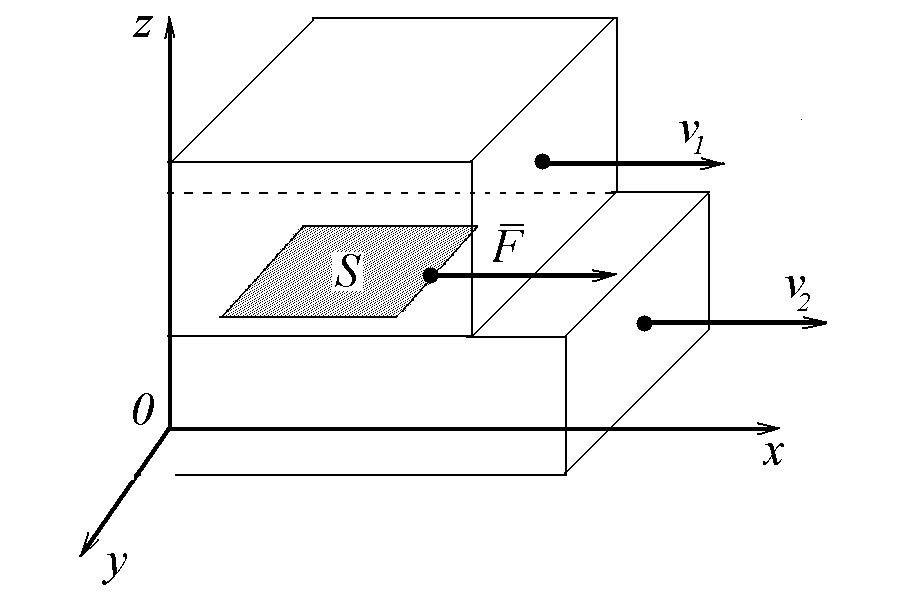
Рис. 21.1. Движение слоев жидкости с разными скоростями

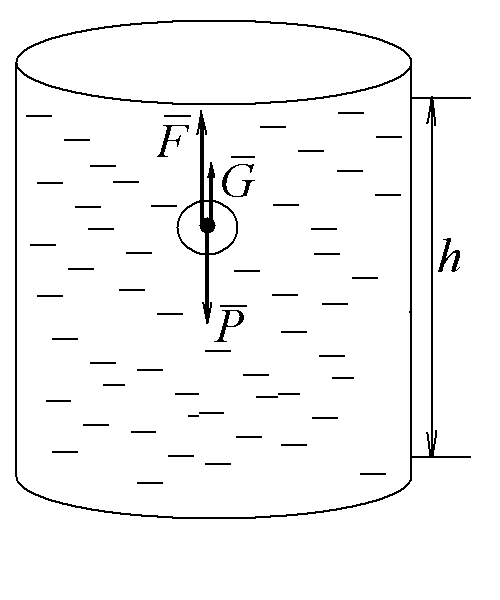
Рис. 21.2. Направление сил, действующих на тело,

находящееся в вязкой жидкости

Вязкая среда оказывает движению тела определенное сопротивление. При малых скоростях и обтекаемой форме тела, когда не возникает вихрей (ламинарное движение), сила сопротивления обусловлена вязкостью жидкости. Слой жидкости, непосредственно прилегающий к твердому телу, прилипает к поверхности этого тела и увлекается им полностью. Следующий слой жидкости увлекается за телом с меньшей скоростью. Таким образом, между слоями вдоль движения возникают силы трения. Для шаров, движущихся в вязкой жидкости, по закону Стокса значение силы сопротивления

F = 6rv , (2)

где  — коэффициент вязкости жидкости, r — радиус шара, v — скорость движения шара.

На шарик, падающий в вязкой покоящейся жидкости, действуют три силы.

1. Сила тяжести P = mg = V_шg = 4/3r³g, где _ш — плотность материала шарика, g — ускорение свободного падения, V — объем шарика.

2. Выталкивающая сила G, равная по закону Архимеда весу вытесненной шариком жидкости: G = V_жg = 4/3r³_жg, где _ж — плотность жидкости.

3. Сила сопротивления движению шарика (Стоксова сила): F = 6rv, где  — коэффициент вязкости жидкости, v — скорость равномерного движения шара.

Направление действия этих сил показано на рис. 21.2.

Почти весь путь в вязкой жидкости тело движется равномерно со скоростью v, поэтому силы уравновешивают друг друга. Имеем

P – G = F; 4/3r³(_ш – _ж) = 6rv₀ (3)

Такое движение называется установившимся.

Решая уравнение (3) относительно коэффициента внутреннего трения , получим.

. (4)

Измеряя скорость установившегося движения v₀ и зная плотности шарика и жидкости и радиус шарика, определяем численное значение коэффициента вязкости жидкости.

С другой стороны, из формулы (1) определяем характерное значение производной скорости жидкости, увлекаемой шариком.

,

где S = 4r² — площадь поверхности шарика.

Считая, что dv/dz = v₀/l, где l — толщина увлекаемого шариком слоя и из F = P – G для установившегося движения в этом приближении, получаем

. (5)

Таким образом, измеряя скорость установившегося движения v₀ шарика радиуса r, и зная коэффициент вязкости , определяем толщину слоя, увлекаемого шариком.

Если в формулу (5) подставить (4), то получим, что толщина увлекаемого слоя для шара l  2r/3.

Порядок выполнения работы

1. Возьмите шарик и при помощи микрометра определите его диаметр d. Вычислите радиус шарика r = d/2, где d — диаметр шарика.

2. Опустите шарик в цилиндр с вязкой жидкостью. С помощью секундомера определите время t прохождения шариком пути h; скорость установившегося движения вычислите по формуле v₀ = h/t.

Примечание. Верхняя метка на цилиндре с вязкой жидкостью располагается на 58 см ниже уровня жидкости. Поэтому считайте, что, начиная с верхней метки, движение шарика уже установилось.

3. Проделайте такие измерения для 5 шариков с различными диаметрами.

4. Вычислите по формуле (4) коэффициент вязкости жидкости. Плотность материала шариков и жидкости указана на установке; ускорение свободного падения g = 9,82 м/с² (для нашей широты).

5. Данные опытов и результаты измерений занести в табл. 21.1.

Таблица 21.1.

Таблица экспериментальных результатов для определения коэффициента вязкости жидкости

№ п/п	h, м	r, м	t, c	v0, м/с	, Па·с	i-cp Па·с	(i-cp)2 Па2·с2
1
2
3
4
5
среднее	-	-	-	-		-

6. Начертите графики (см. п.1.3. Общих указаний) зависимости. Поставьте погрешности для  = f(r) и v₀ = f(r), где r — радиус шариков.

7. Определите погрешность измеренного значения коэффициента вязкости. Действуйте в соответствии с «Порядком обработки результатов прямых измерений (п.2.2 в Общих рекомендациях). Для пяти измерений коэффициент Стьюдента K_S =2,8.

8. Окончательный результат запишите в виде  = (Па·с).

Контрольные вопросы

1. Какова природа внутреннего трения?

2. Какие силы действуют на шарик, движущийся в вязкой жидкости?

3. Поясните, почему движение шарика в жидкости через некоторое время становится равномерным?

4. Как зависит коэффициент вязкости жидкости  от радиуса и материала, из которого сделан шарик?

5. Чему равна потенциальная энергия силы вязкого трения?