Задание 1 Получение функции распределения электронов по скоростям
В данной лабораторной работе для исследования вида функции распределения по скоростям предлагается метод задерживающего потенциала.
Основной частью схемы является электронная лампа диод с подогреваемым катодом. Диод имеет катод (К), анод (А) и спираль подогрева катода (см. рис. 20.3).
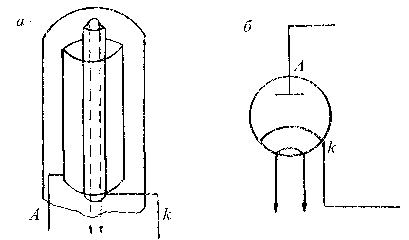
Рис. 20.3. Схематическое устройство лампы диод (а)
и ее изображение на схемах (б)
Как видно из рис. 20.3, диод имеет цилиндрическую симметрию. При нагревании электрическим током катода лампы из него вылетают электроны с разными по направлению и величине скоростями. Этот электронный газ подчиняется статистике Максвелла. С учетом цилиндрической симметрии диода число электронов, имеющих скорость в интервале скоростей от v до v + dv, как показывает теория, равно
. (8)
В лаборатории используется следующая принципиальная схема (рис. 20.4).
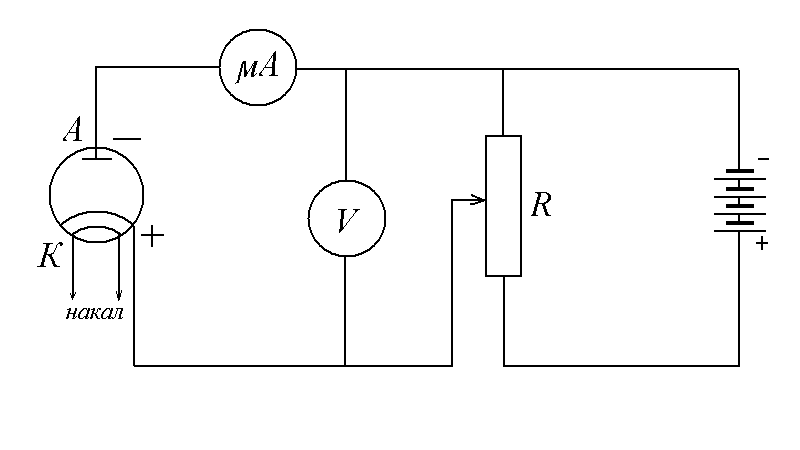
Рис. 20.4. Принципиальная схема установки
(цепь накала катода не изображена)
В ней на анод подается отрицательный потенциал от источника тока, а на катод — положительный. Если разность потенциалов между катодом и анодом U = 0, то вырванные с поверхности катода электроны, у которых достаточная кинетическая энергия mv2/2, способны долететь до анода и создать в анодной цепи ток I0, который можно измерять микроамперметром. Если отрицательное напряжение между анодом и катодом U будет расти, то число электронов, способных преодолеть задерживающее поле будет уменьшаться. Преодолевают задерживающее поле и создают ток I в анодной цепи только электроны с энергией
, (9)
где e — заряд электрона, U — разность потенциалов между анодом и катодом.
При этом кинетическая энергия электрона тратится на работу против сил электрического поля.
Зная
U,
можно судить о величине скорости
электронов. скорость электронов,
прошедших задерживающее поле,
пропорциональна
,
т. е. v
~
.
Обозначим
= x;
тогда v
= x,
где
— некоторый
коэффициент. Величина тока в цепи (I)
пропорциональна числу электронов,
достигающих анода в единицу времени I
~N/t.
Построим график I
= f(x)
(рис. 20.5).
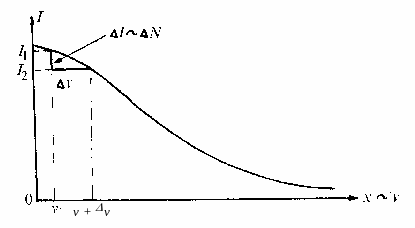
Рис. 20.5. График зависимости I = f(x)
На рис. 20.5 возьмем некоторое значение абсциссы x; оно пропорционально некоторой скорости v, близкая к ней абсцисса графика пропорциональна v + v. При этом приращение ординаты |I2 – I1| = I пропорционально числу электронов, имеющих скорость в интервале от v до v + v. Если разделить приращение ординаты I на приращение абсциссы x и построить график I/x = (v), он будет иметь вид функции N/v = (v) c точностью до постоянного множителя, совпадающей с распределением Максвелла. Такое преобразование графика называется графическим дифференцированием.
Практически оно делается так, как показано на рис. 20.6.
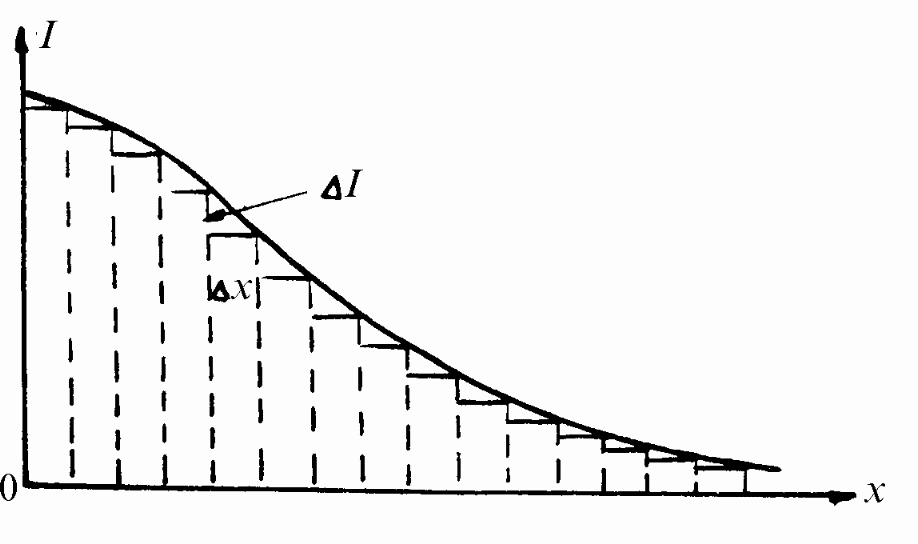
Рис. 20.6. Графическое дифференцирование функции I = (x)
Абсцисса графика I = (x) разбивается на достаточно малые равные промежутки x (их должно быть не менее 15), находятся соответствующие им приращения ординат графика I (по линейке в миллиметрах) и строят график I = f(x) (если все x равны, можно не производить деления I на x).
Этот график имеет вид распределения Максвелла (рис. 20.7), если соединить точки плавной кривой.
Напомним, что площадь под кривой рис. 20.7 численно равна числу всех электронов, прошедших задерживающее поле и имеющих скорость в интервале от 0 до.
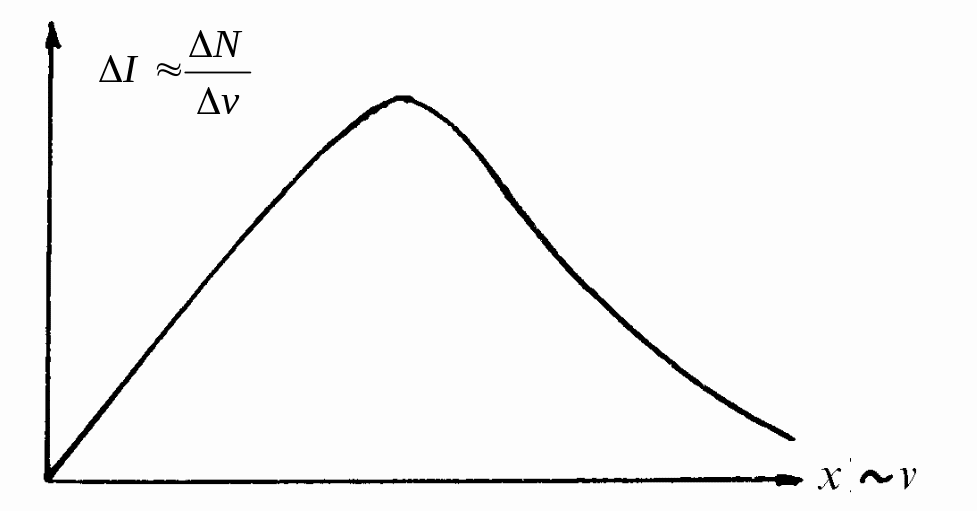
Рис. 20.7. Экспериментально полученный график
функции распределения Максвелла