Молекулярная физика Лабораторная работа № 20 распределение максвелла

Цель работы

Получение и изучение распределения Максвелла для электронного газа.

Оборудование

1. Электронная лампа (диод с подогреваемым катодом);

2. Источник напряжения на 0,5 В;

3. Микроамперметр на 200 А для измерения анодного тока;

4. Вольтметр на 0,5 В;

5. Цепь накала: источник постоянного напряжения на 4—8 В, миллиамперметр на 500 mA, вольтметр на 15 В, реостат 25 Ом 5 А.

Основные сведения

В замкнутом сосуде, наполненном газом (например, газом электронов), устанавливается термодинамическое равновесие, которое характеризуется определенным распределением молекул газа по скоростям. Известно, что средняя кинетическая энергия беспорядочного движения молекул газа прямо пропорциональна его абсолютной температуре

. (1)

Отсюда следует, что средняя квадратичная скорость для газа из частиц, не имеющих составных частей,

, (2)

где k = 1,38 10^23 Дж/К — постоянная Больцмана, T — абсолютная температура газа, m — масса молекулы газа. Для двухатомных молекул в формуле (2) стоит число 5.

При t=15°C средняя квадратичная скорость v_кв молекул азота (N₂) равна ~500 м/c; со скоростями от 300 до 700 м/c движется 59% молекул. С малыми скоростями — от 0 до 100 м/c — движется лишь 0,6% молекул. Быстрых молекул со скоростями свыше 1000 м/c в газе всего лишь 5,4 %. При нормальных условиях каждая молекула претерпевает в секунду примерно 10⁹ соударений и, следовательно, величина и направление скорости каждой молекулы изменяются. Это перераспределение скоростей между молекулами происходит так, что число молекул, обладающих значениями скорости, заключенной в определенном интервале, все время остается постоянным и описывается распределением по скоростям Максвелла.

Рассмотрим, что представляет собой это распределение. Пусть данная масса газа содержит N молекул. Тогда число молекул dN, скорости которых имеют значение от v до v + dv (т. е. заключены внутри интервала dv), очевидно, пропорционально рассматриваемому количеству молекул. Вместе с тем оно пропорционально и величине заданного интервала dv и, конечно, будет зависеть от самого значения скорости v, т. е. dN = N F(v) dv, где F(v) — функция, характеризующая распределение молекул газа по скоростям.

(3)

и есть функция распределения, численно равная относительному числу молекул, имеющих скорость в интервале от v до v + dv, отнесенному к величине этого интервала скоростей dv.

Отношение dN/N = F(v) dv дает вероятность того, что скорость молекулы будет иметь значение в пределах данного интервала скоростей dv.

Если проинтегрировать dN по всем интервалам dv, на которые разбиты возможные значения скорости v, то, очевидно, можно получить полное число молекул N. Отсюда вытекает следующее свойство функции распределения.

, (4)

которое получило название условия нормировки функции.

Оно имеет смысл того, что молекула имеет одно из значений скорости в пределах от 0 до . Так как скорость молекулы, несомненно, имеет какое-либо значение, то указанная вероятность есть вероятность достоверного события и, следовательно, равна 1. Функцию распределения молекул по скоростям (распределение Максвелла) записывают в виде

, (5)

где А — множитель, не зависящий от v (его значение можно найти из условия нормировки функции распределения).

Функция F(v) стремится к  0 при v  0 и v  ; ее график имеет следующий вид.

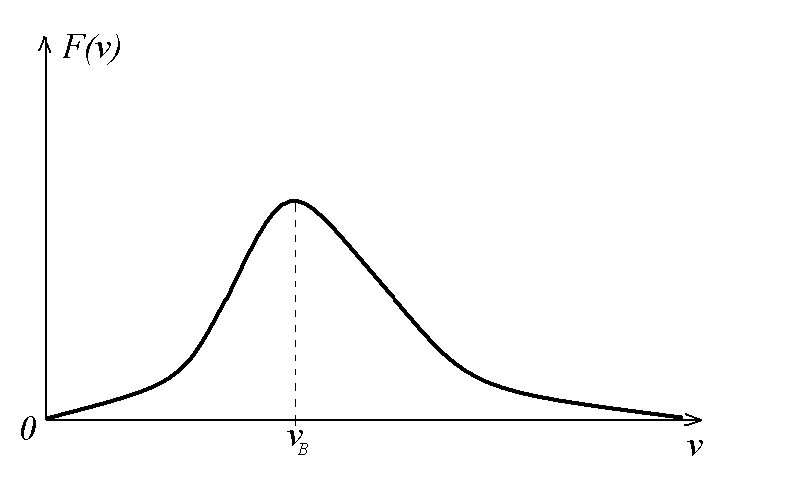
Рис. 20.1. График функции распределения Максвелла

Скорость, которая соответствует максимуму функции распределения, называется наиболее вероятной — v_в. Чтобы ее найти, нужно продифференцировать функцию распределения F(v) (см.(5)) по v и приравнять полученное выражение к 0, т. е. обычным путем, как находится максимум функции в математике. Оказывается

(6)

Сравнивая (6) и (2), имеем

. (7)

Наибольшее число молекул имеют скорости в том интервале, к которому относится наиболее вероятная скорость. При возрастании температуры наиболее вероятная скорость увеличивается пропорционально  (см. формулу (6)) и максимум распределения сдвигается вправо (см. рис. 20.3?).

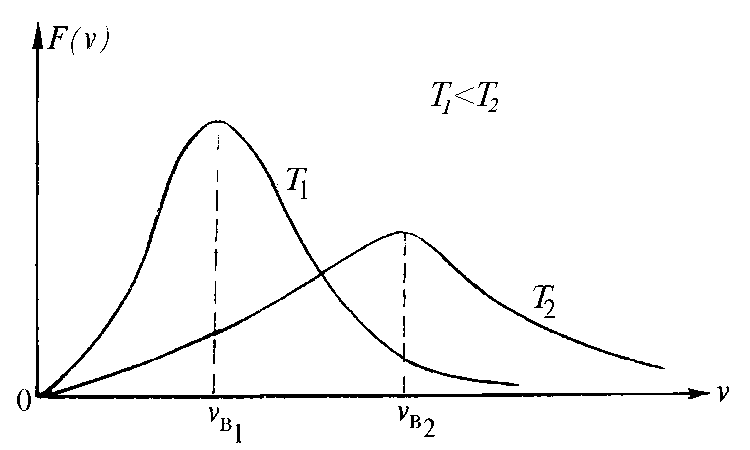
Рис. 20.3?. Графики функции распределения Максвелла разных температур газа

При этом число медленных молекул убывает, а число быстрых возрастает, но площадь под кривой остается постоянной, равной 1.