Лабораторная работа № 13 определение момента инерции тела методом крутильных колебаний

Формула этана, который встречается в больших количествах в природном газе некоторых месторождений, С₂H₆. Его строение представлено на рис. 13.1, где указаны длины валентных связей С—С и C—H. Атомы в молекуле этана способны совершать крутильные колебания.

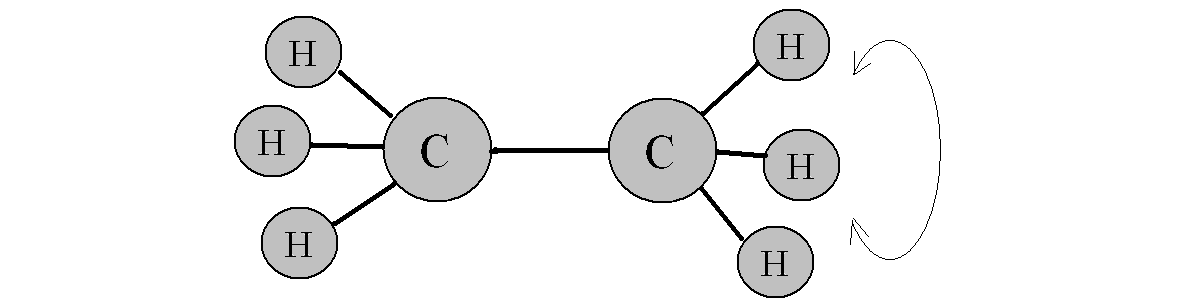
Рис. 13.1. Строение этана

Если зафиксировать одну из молекулярных групп, то вторая может совершать торсионные колебания (от франц. torsion — кручение), которые моделируются крутильными колебаниями диска на нити.

Поэтому полезно познакомиться с крутильными колебаниями, провести их аналогию с гармоническим колебательным движением и выяснить еще один метод определения момента инерции тела.

Выполнение работы на установке №1

Цель работы

Определить момент инерции тела (диска, шара, кольца).

Оборудование

1. Установка для изучения крутильных колебаний диска и надетого на него кольца.

2. Секундомер.

3. Штангенциркуль, линейка.

Основные сведения

Во вращательном движении, в отличие от поступательного, инерционные свойства тел характеризуются не массой, а особой физической величиной, называемой моментом инерции I. Произведение массы материальной точки m на квадрат ее расстояния R² от оси вращения называется моментом инерции материальной точки I = mR² . Если любое тело сложной формы мысленно разбить на n элементов (материальных точек), то момент инерции всего тела можно вычислить как сумму моментов инерции его элементов

, (1)

где i — номер элемента тела.

Момент инерции тела зависит от размеров и формы тела, а также от распределения его массы относительно оси вращения. Одно и то же тело, вращаясь относительно различных осей, будет обладать различными моментами инерции. В СИ момент инерции, как видно из формулы, измеряется в кг·м².

В общем случае вычисление момента инерции тела представляет собой сложную задачу, решаемую с помощью интегрирования. Сравнительно легко можно найти моменты инерции тел правильной геометрической формы, состоящих из однородного вещества. Например, момент инерции сплошного диска относительно оси, проходящей через его центр,

, (2)

где m — масса диска, R — его радиус.

Момент инерции сплошного шара радиусом R и массой m, относительно оси, проходящей через его центр.

, (3)

Если кольцо имеет правильную форму, его момент инерции относительно оси, проходящей через его центр можно рассчитать теоретически по формуле.

, (4)

где m_k — масса кольца, R₁ и R₂ — внешний и внутренний радиусы кольца.

Часто моменты инерции различных тел определяют экспериментально. В нашей работе это делают с помощью метода крутильных колебаний. Если тело подвесить на упругом подвесе и, закрутив его на малый угол (не более 5—10 градусов), предоставить систему самой себе, она будет совершать крутильные колебания (см. рис. 13.2).

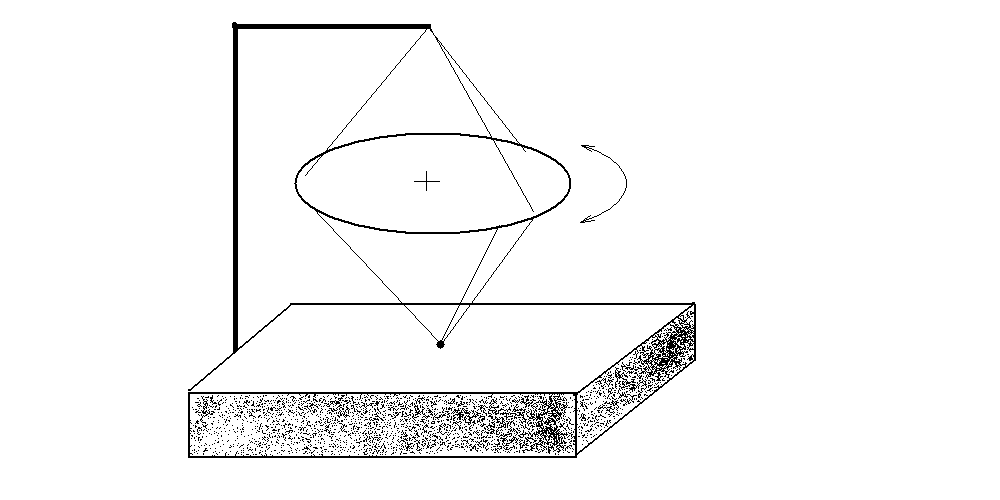
Рис. 13.2. Схема лабораторной установки

Как известно, при колебательном движении тела массой m на пружине жесткостью k период колебаний T равен

. (5)

(Напомним, что период колебаний — время одного полного колебания, т. е. движения тела «туда и обратно».) При крутильных колебаниях роль массы играет момент инерции I, а роль жесткости k — коэффициент кручения f, зависящий от упругих свойств подвеса. Тогда период крутильных колебаний - период колебаний маятника

. (6)

Момент инерции тела (диска, шара, кольца) I_тела можно определить, используя метод сравнения периода крутильных колебаний маятника без тела I_{маятника} и период крутильных колебаний исследуемого тела совместно с маятником. Действительно, при совместном колебании маятника и тела момент инерции системы будет

I = I_{маятника} + I_тела. (7)

Период колебаний маятника с добавленным телом станет

T = . (8)

Возведя равенства (6) и (8) в квадрат и разделив одно на другое, получим.

. (9)

Выразив из последнего равенства I _тела, получим

, (10)

Так как маятник имеет форму диска, то

I_{маятника} = ,

(cм. формулу 2), то окончательно

, (11)

где m_м — масса маятника: у диска указана на установке, R_м — радиус маятника диска, (измеряется линейкой), T_{маятника} — период колебаний пустого маятника (измеряется с помощью секундомера), T — период колебаний маятника совместно с измеряемым телом (измеряется также секундомером).

Описание установки

Схема установки приведена на рис. 13.2 и рис. 13.3.

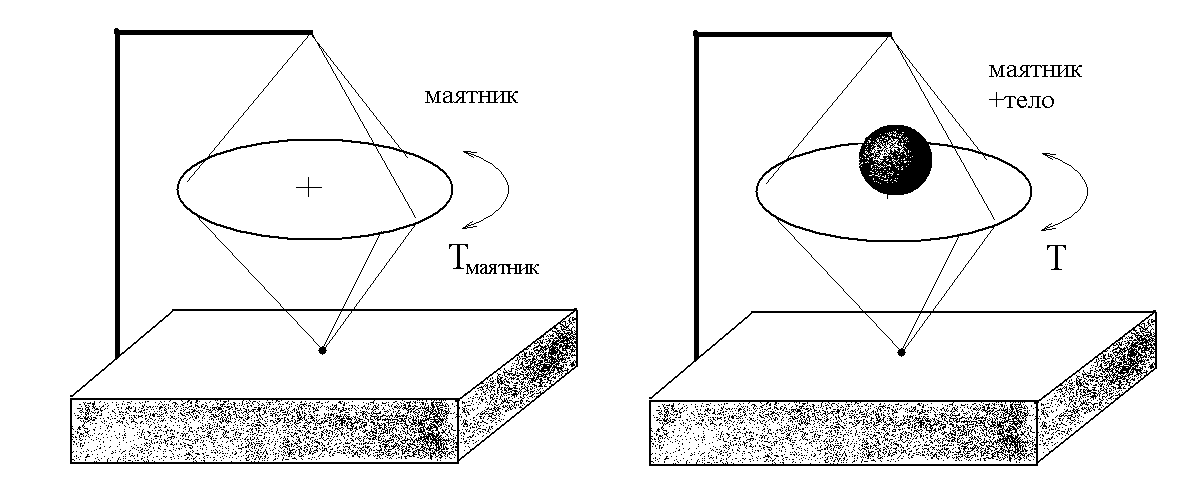
Рис. 13.3. Варианты используемой установки

Она состоит из крутильного маятника, подвешенного на проволоке, и тела, которое можно подвесить на диск.

Порядок выполнения работы

1. Определить период колебаний маятника без тела T_{маятника} (cм. рис. 13.3а). Для этого поверните диск на угол ~10°, затем, отпустив его, дайте ему совершать крутильные колебания. Измерьте время t 20-ти полных колебаний (движение «туда и обратно»). Опыт повторить 5 раз. При этом n — число колебаний диска.

2. Данные занести в табл. 13.1.

3. Поместите исследуемое тело на маятник. Следите, чтобы тело располагалось точно по центру маятника.

4. Аналогично найдите период колебаний T вместе с исследуемым телом (см. рис. 13.3.б)

5. Данные занесите в табл. 13.1.

Таблица 13.1