Потенциальная энергия тела в поле тяготения Земли
Тяготение Земли
создается гравитационной силой, величина
которой равна
.
«Нулевой конфигурацией», то есть
состоянием, в котором поле тяготения
не действует на тело, является бесконечно
удаленная точка. При перемещении тела
из бесконечности в точку r
сила тяготения направлена вдоль
перемещения, поэтому cos (F
^ dх)
= cos0=l и
Итак, потенциальная энергия тела т в поле тяготения Земли М отрицательна, пропорциональна произведению масс и обратно пропорциональна расстоянию между центрами тел:
.
(2.5)
Поскольку расстояние r не меньше радиуса Земли R, потенциальная энергия тела в поле тяготения Земли имеет вид, представленный на рис. 2.2.
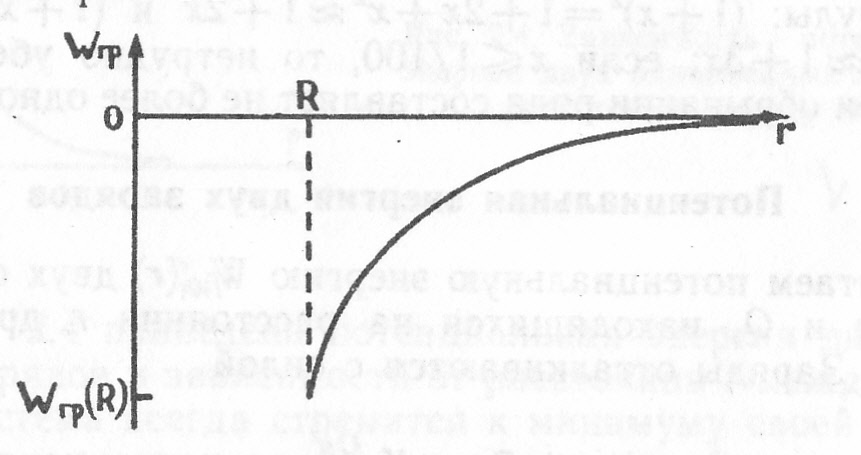
Рис. 2.2. Зависимость потенциальной энергии тела
от расстояния до центра Земли
Чтобы полностью
покинуть Землю (улететь от Земли на
другие планеты Солнечной системы),
кинетическая энергия тела должна
превышать потенциальную энергию
тяготения Wгр(R)
на поверхности Земли, т. е.
.
Необходимая для этого скорость должна
быть больше величины
км/с . (2.6)
Эта скорость называется второй космической. Достичь такой скорости и добиться того, чтобы тела улетали с Земли к другим планетам, удалось только в последние десятилетия.
Потенциальная энергия тела на высоте h от поверхности Земли
Рассмотрим потенциальную энергию тела на высоте h от поверхности Земли (при h«R). Расстояние от центра Земли до тела равно r = R+h. Тогда
(2.7)
IV/ /1,4 „ тМ тМ /, ,
На поверхности
Земли потенциальная энергия тела
минимальна и равна
.
Учитывая, что g=γM/R2,
из формулы 2.7 получаем соотношение:
Wгр(h)Wгp(R)+mgh, (2.8)
справедливое для тел, находящихся вблизи поверхности Земли.
При выводе формулы 2.7 мы использовали разложение в ряд функции (1+x)α 1+αх + …, справедливое для х«1. Чтобы пояснить смысл такого разложения в ряд, напомним Вам известные формулы: (l+x)2= 1+2х+х2 1+2х и (1+х)3=1+3х+3х2+х3 1+Зх; если x≤1/100, то нетрудно убедиться, что ошибка при обрывании ряда составлявляет не более одного процента.
Потенциальная энергия двух зарядов
Рассчитаем потенциальную энергию Wэл(r) двух одноименных зарядов q и Q, находящихся на расстоянии r друг от друга (рис 2.3). Заряды отталкиваются с силой
. (2.9)
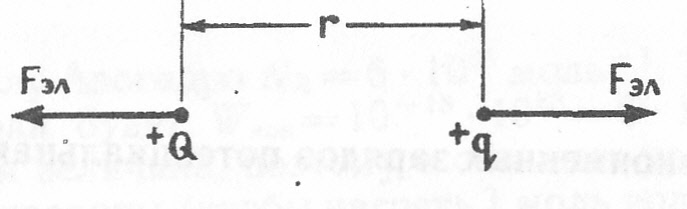
Рис 2.3. Силы, действующие между одноименными зарядами
Коэффициент пропорциональности К зависит от выбора единиц измерения зарядов. В СИ заряды измеряются в кулонах (Кл) и К = 9·109 Н·м/Кл2.
Чтобы перевести заряд q из «нулевой конфигурации», т.е. из бесконечности в точку r, надо совершить работу
(2.10)
по преодолению электрической силы отталкивающихся зарядов. Знак минус связан с тем, что (Fэл^dr)=cosπ=-1, т. к. сила и перемещение противоположно направлены. Подставляя (2.9) в (2 10), имеем
. (2.11)
Следовательно, потенциальная энергия двух одноименных точечных зарядов пропорциональна произведению зарядов и обратно пропорциональна расстоянию между ними:
. (2.12)
Рис 2 4 Зависимость потенциальной энергии двух одноименных зарядов
от расстояния между ними
На рис 2 4 приведена потенциальная энергия двух положительных зарядов в зависимости от расстояния r между ними. Поскольку система всегда стремится к минимуму своей энергии, то ясно, что одноименные заряды стремятся разойтись друг от друга на большое расстояние.
Для двух разноименных зарядов потенциальная энергия равна
. (2.13)
Положительная потенциальная энергия означает, что для сближения зарядов требуется затратить работу. Отрицательная потенциальная энергия означает, что работа будет затрачиваться при удалении зарядов друг от друга.
З а д а н и е: нарисуйте зависимость потенциальной энергии двух зарядов от расстояния.