Домашнее задание.

Задание 7. Составить уравнение плоскости, проходящей через точку и

а) перпендикулярной вектору ;

б) параллельной плоскости ;

в) точки , .

Задание 8. Составить уравнение прямой, проходящей через точку и

а) точку ;

б) параллельно прямой .

7) а) –x-y+2z+11=0, б) 2x-y+z=0, в) y+z-2=0;

8) а) , б) .

Вычисление простейших пределов. Краткие теоретические сведения.

Рассмотрим последовательность , где n=1, 2, 3, …:

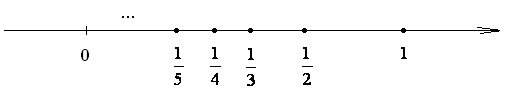
Видим, что все члены последовательности , но чем больше номер n, тем ближе расположен к нулю. Этот факт записывают следующим образом:

; ; .

И говорят, что предел последовательности равен 0.

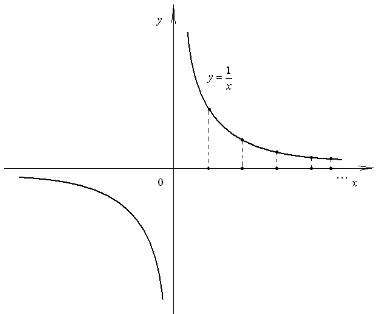
Аналогично можно найти пределы функции :

или .

Говорят, что «предел функции при x, стремящемся к равен 0».

Рассмотрим несколько примеров пределов функций:

,

,

Предел функции может и не существовать. Например:

	не существует, т.к. при значение функции не стремятся к какому-нибудь определенному значению, а периодически меняются от -1 до 1.
	не существует, т.к. если х стремится к 0 слева, то значение функции стремится к , а справа – к Единого значения предела при нет.

При вычислении пределов часто возникают выражения:

- определенные , .

- неопределенные , , , , , .

Алгоритм нахождения пределов функций :

Шаг 1. Подставить значение в формулу задания .

Если получится вполне определенный результат, то это и есть значение предела при . Если же возникает неопределенность, то перейти к следующему шагу.

Шаг 2. Раскрыть неопределенность с помощью тождественных преобразований выражения . Так, если в числителе и знаменателе находятся многочлены и возникает неопределенность вида , то следует разложить числитель и знаменатель дроби на множители и сократить на множитель .

Если в числителе и знаменателе находятся многочлены и возникает неопределенность , то следует разделить числитель и знаменатель на х с наибольшим показателем степени числителя и знаменателя.

Шаг 3. Вновь подставить в преобразование выражение и определить значение предела .

Решение типовых заданий

Задание 1. Найти .

Решение:

Шаг 1. Подставим в функцию :

- неопределенность.

Шаг 2. Разложим числитель и знаменатель на множители и сократим на множитель:

Шаг 3. Вновь подставим :

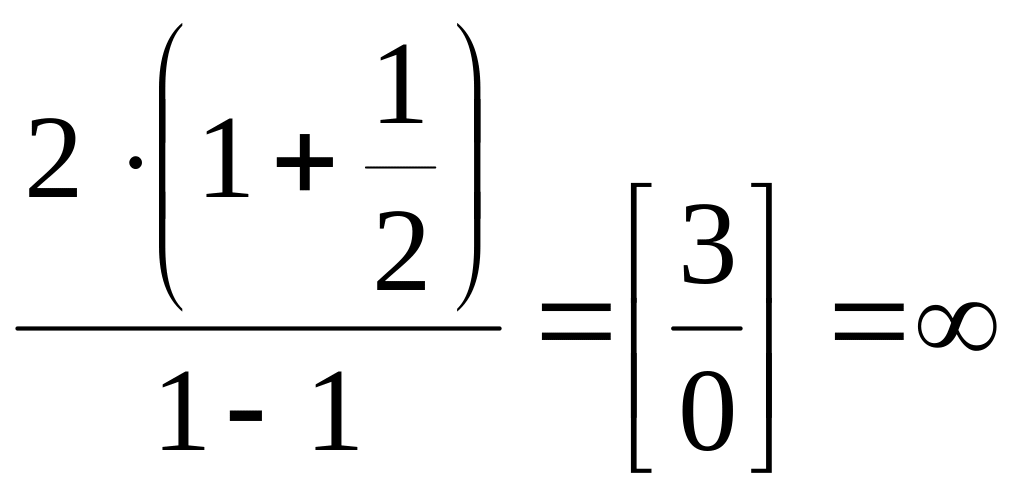, следовательно

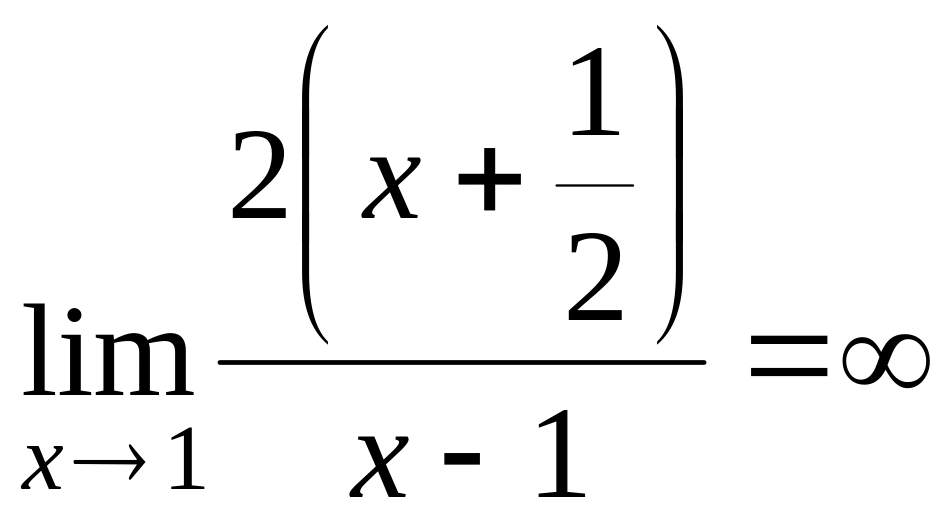т.е. .

Задание 2. Найти .

Решение:

Шаг 1. Подставим в функцию , получим неопределенность .

Шаг 2. Т.к. поведение числителя и знаменателя при определяется членами с наибольшими показателями степеней, разделим числитель и знаменатель на :

.

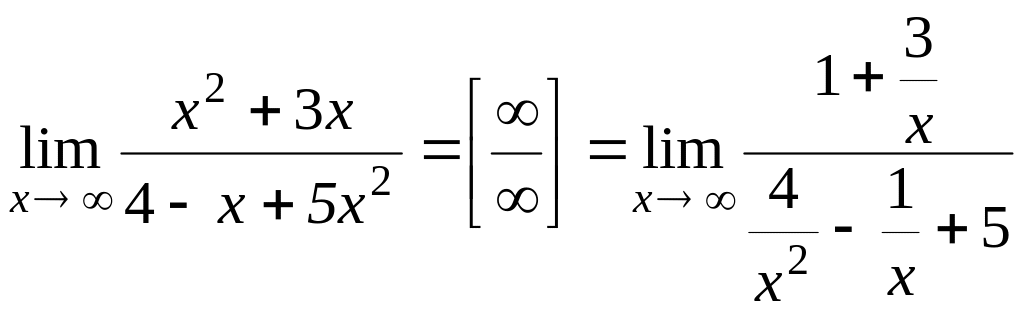Шаг 3. Вновь подставим в функцию. Учитывая, что , получим .

Т.о.

Задание 3. Найти .

Решение:

Шаг 1. подставим выражение

- неопределенность.

Шаг 2. В отличие от задания №1 в числителе дроби стоит не многочлен, а иррациональное выражение. Умножим числитель и знаменатель дроби не сопряженные числителю иррациональное выражение , упростим и разложим многочлены на множители:

.

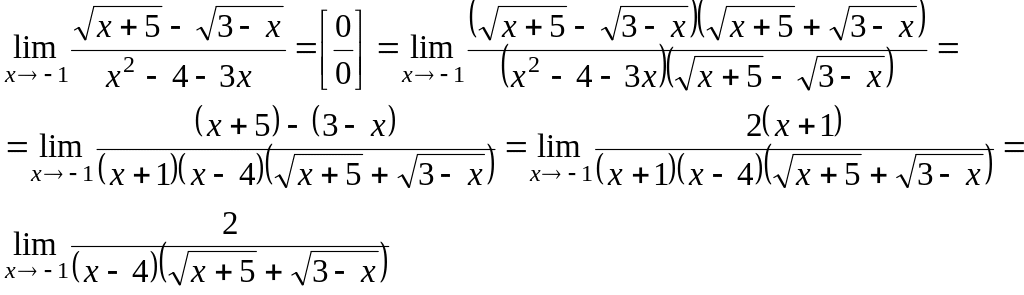Шаг 3. Вновь подставим в выражение:

.

Т.о. .

Задание для самостоятельного решения.

Вычислить следующие пределы:

4.	5.
6.	7.
8.	9.
10.	11.
12.	13.
14.	15.
16.	17.

Ответы: 4) ∞; 5) 0; 6) ; 7) -5; 8) 1,5; 9) ; 10) 0; 11) ; 12) ∞; 13) ; 14) 0; 15) ; 16) 1,5; 17) .

Домашнее задание.

18.	19.
20.	21.
22.	23.

Ответы: 18) ; 19) ; 20) ; 21) ; 22) ; 23) 4.

Вычисление производных.

Краткие теоретические сведения.

Пусть функция определена в окрестности точки и точка принадлежит графику функции. - приращение аргумента - соответствующее приращение функции .

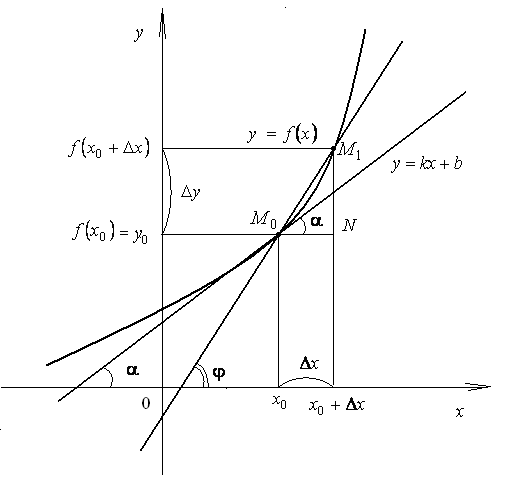
Угол наклона секущей, проходящей через точки и , равен .

Угол наклона касательной к графику т. , равен .

Из , находим .

При угол , а .

Т.о. (1)

Производной функции в точке называют предел (1), если он существует и равен числу. Обозначение производной:

(2)

Из (1) и (2) следует, что угловой коэффициент касательной к графику в точке равен производной функции :

(3)