
- •Прямая на плоскости. Краткие теоретические сведения.
- •Решение типовых заданий.
- •Задания для самостоятельного решения.
- •Домашнее задание.
- •Операции над матрицами. Краткие теоретические сведения.
- •Решение типовых заданий.
- •Задания для самостоятельного решения.
- •Домашнее задание.
- •Определители. Формулы Крамера. Краткие теоретические сведения.
- •Решение типовых заданий.
- •Задания для самостоятельного решения.
- •Решение типовых заданий.
- •Решение типовых заданий.
- •Решение типовых заданий.
- •Решение типовых заданий.
- •Задания для самостоятельного решения.
- •Домашнее задание.
- •Вычисление простейших пределов. Краткие теоретические сведения.
- •Решение типовых заданий
- •Основные правила нахождения производных
- •Решение типовых заданий.
- •Задания для самостоятельного решения.
- •Домашнее задание.
- •Монотонность и экстремумы функции. Краткие теоретические сведения.
- •Решение типовых заданий.
- •Решение типовых заданий.
- •Решение типовых заданий.
- •Решение типовых заданий.
- •Задания для самостоятельного решения.
- •Домашнее задание.
Задания для самостоятельного решения.
Задания
3. Даны матрицы:
![]() ,
,
![]() ,
,
![]() .
.
Найти
матрицы
,
![]() ,
,
![]() ,
,
![]() ,
,
если они существуют.
,
,
если они существуют.
Задания
4. Даны матрицы:
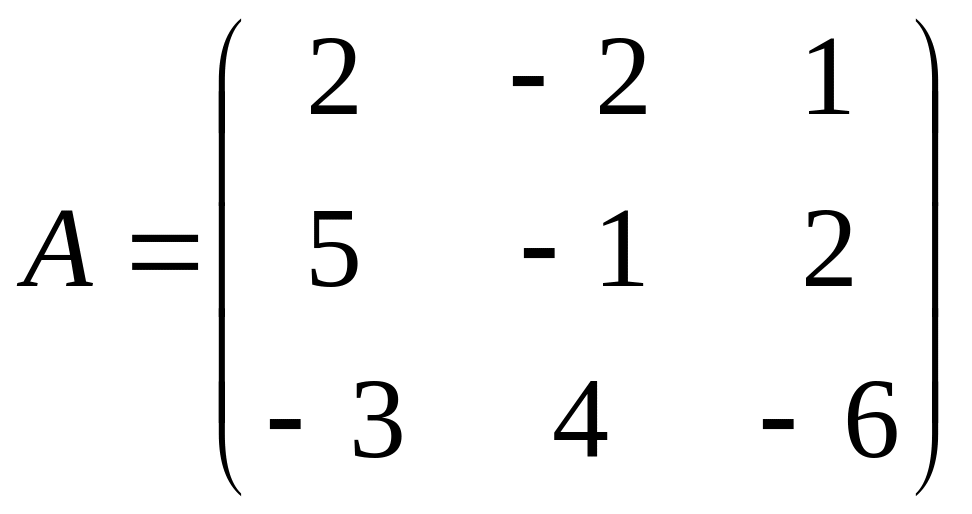 ,
,
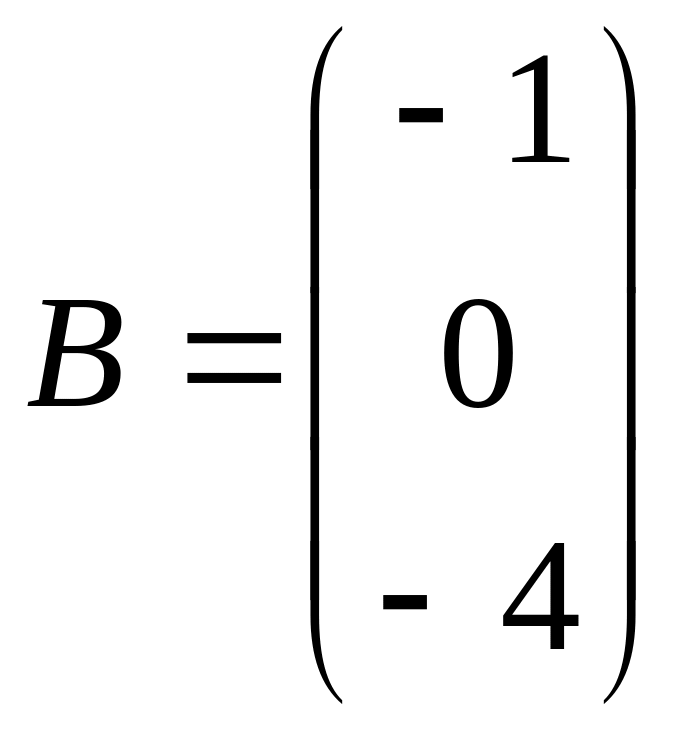 ,
,
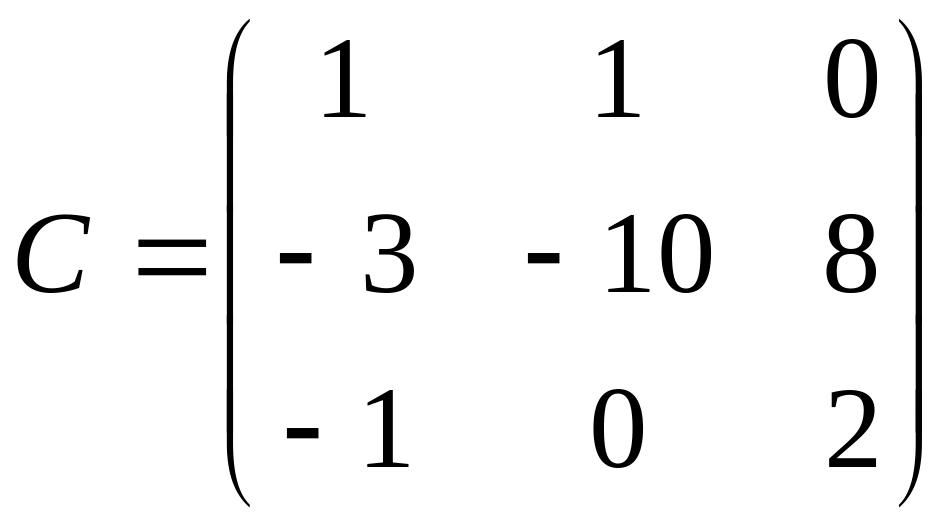 .
.
Найти
матрицы
,
![]() ,
,
,
,
![]() ,
если они существуют.
,
если они существуют.
Задания
5. Даны матрицы:
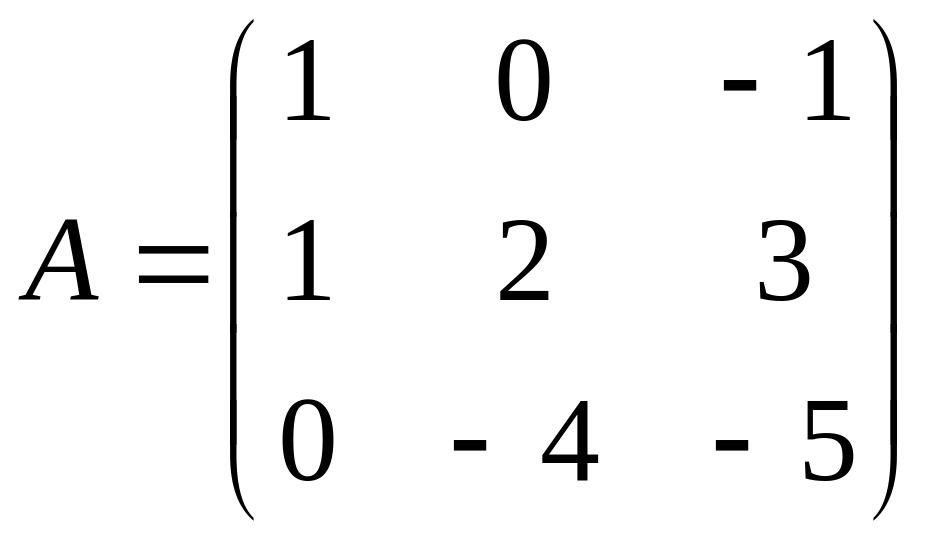 ,
,
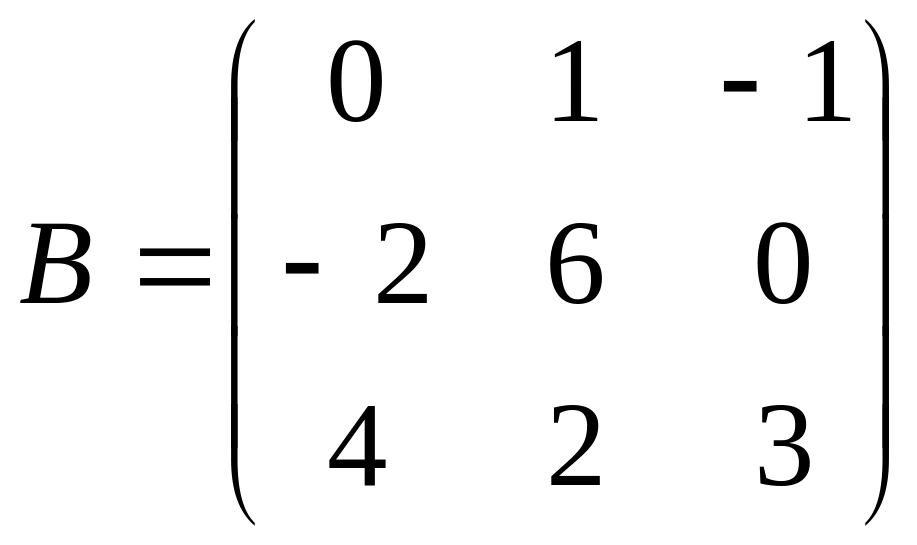 ,
,
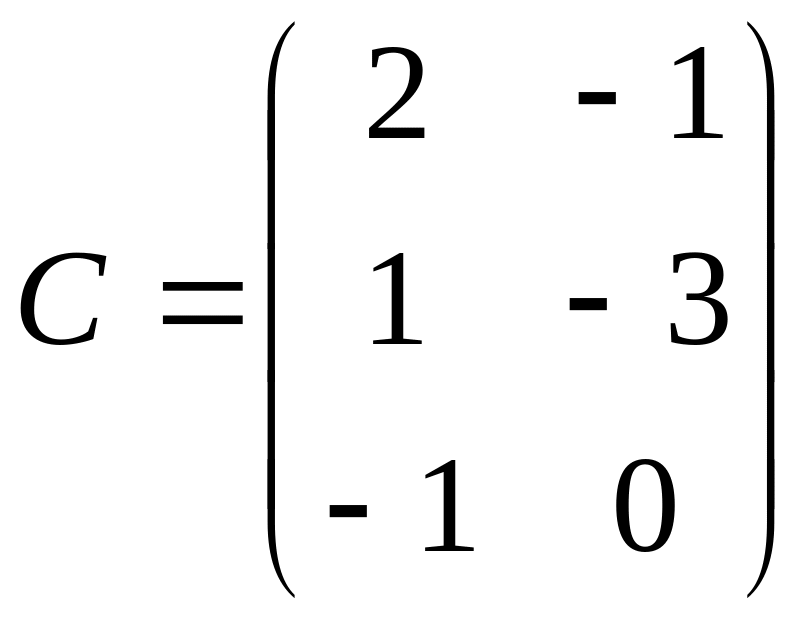 .
.
Найти
матрицы
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() если
они существуют.
если
они существуют.
Задания
6. Даны матрицы:
![]() ,
,
![]() ,
,
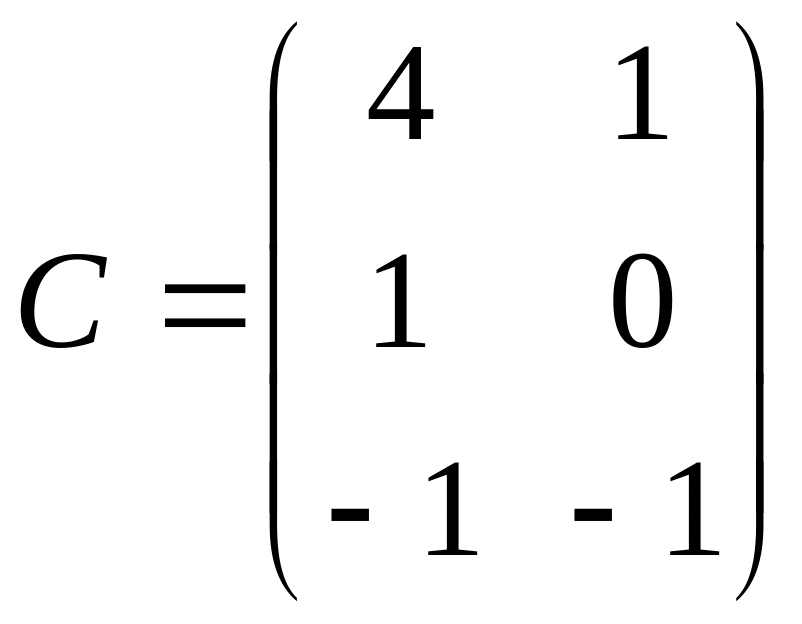 ,
,
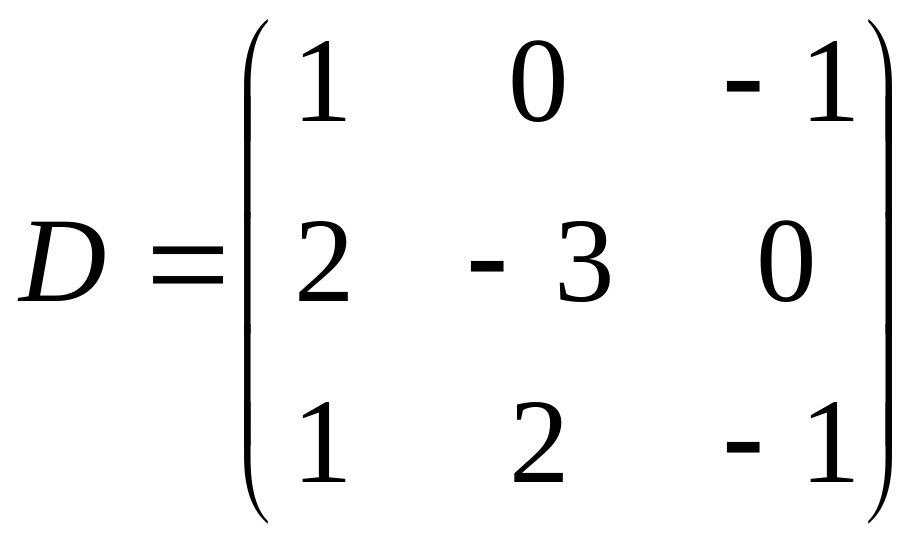 .
.
Найти матрицы |
1)
|
4)
|
|
2)
|
5)
|
|
3)
|
6)
|
Ответы:
3) AB=![]() ,
BC
– не существует, B–C=
,
BC
– не существует, B–C=![]() ,
3A=
,
3A=![]() ,
A+B
– не существует; 4) AB=
,
A+B
– не существует; 4) AB=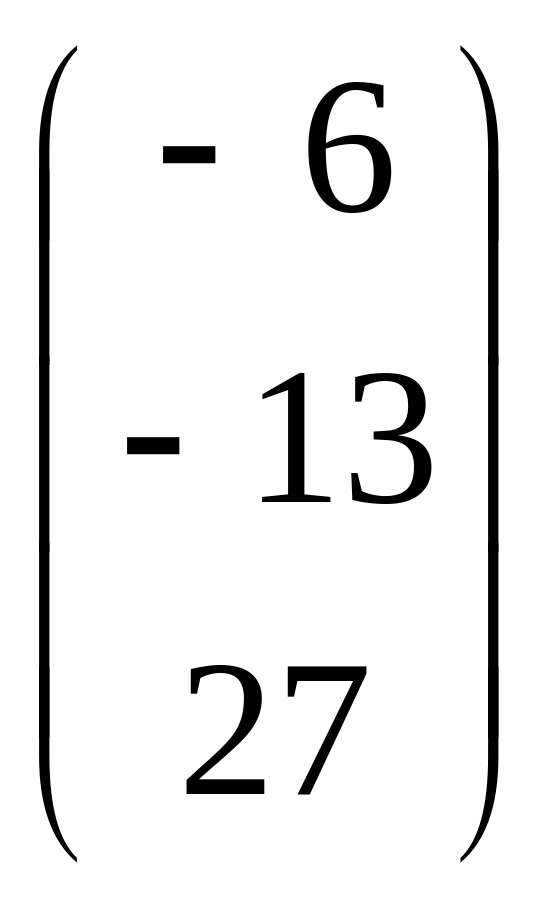 ,
A+2C=
,
A+2C=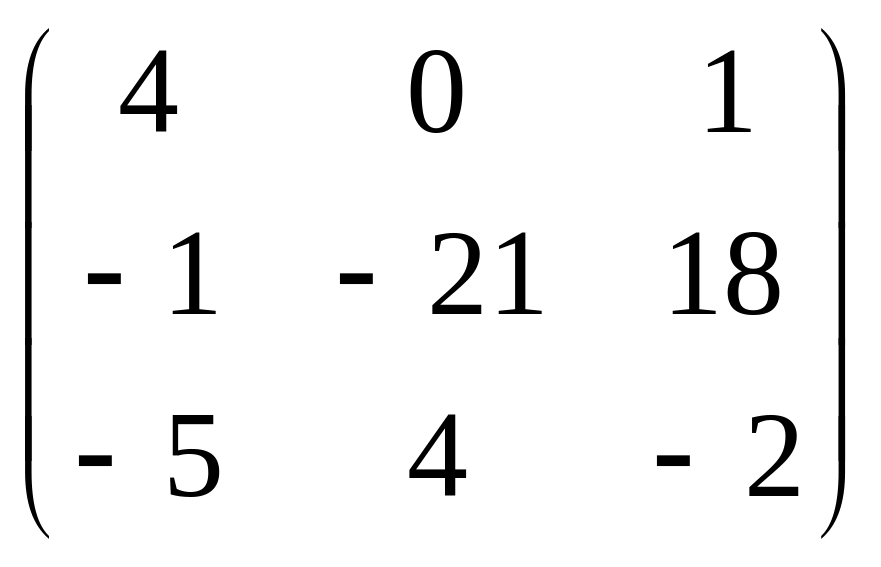 ,
BC
– не существует, AC=
,
BC
– не существует, AC=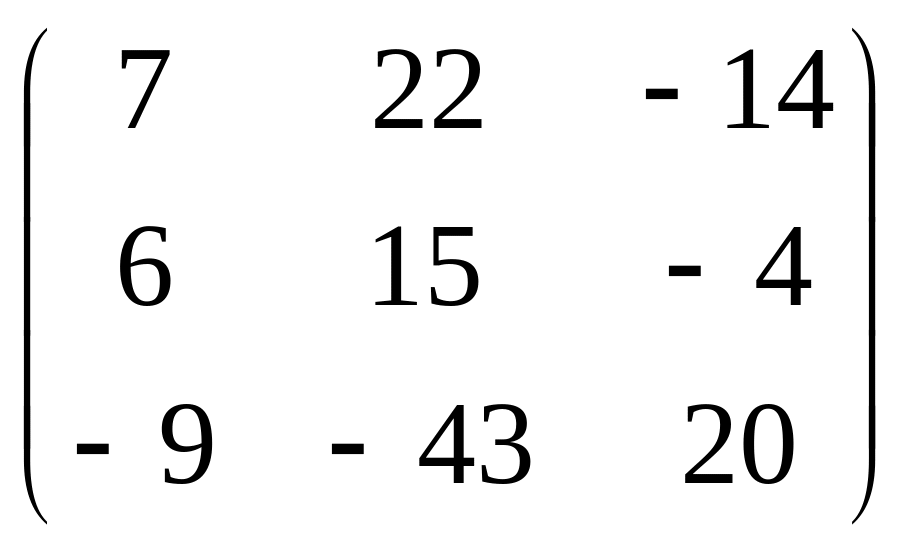 ,
B+C
– не существует;
,
B+C
– не существует;
5)
![]() ,
ABC=
,
ABC=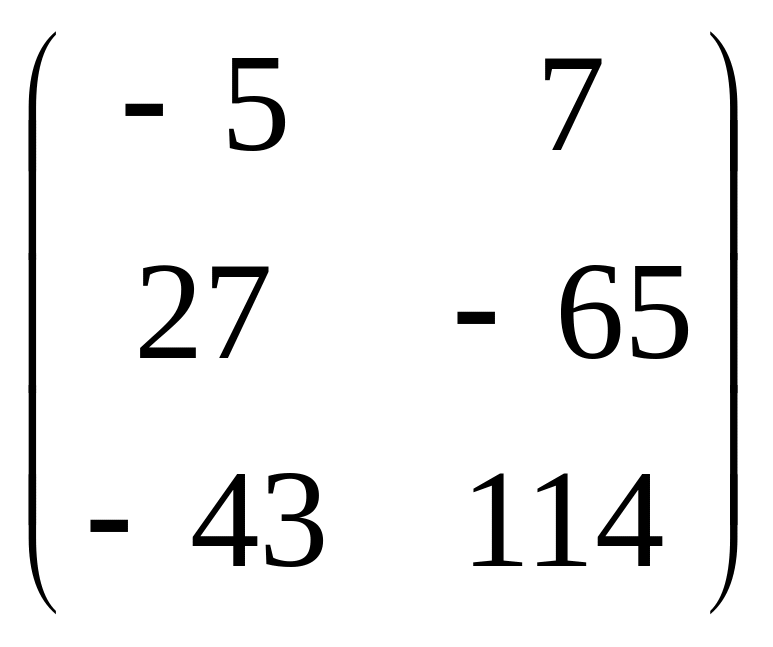 ,
,
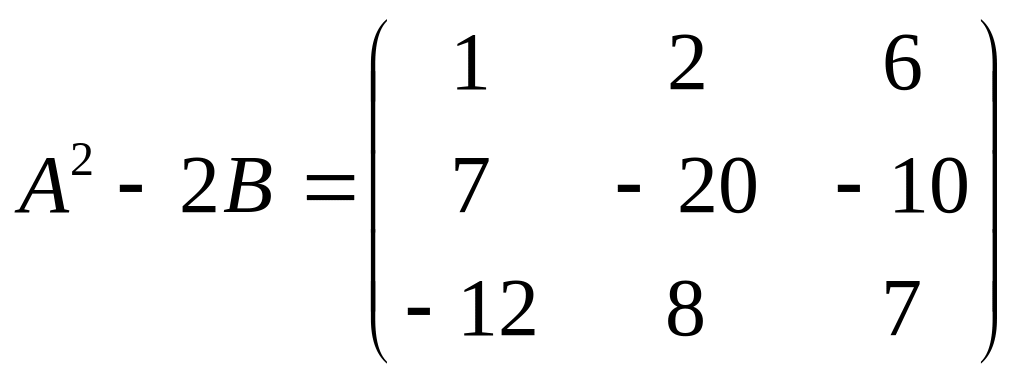 ,
,
ACB
– не существует,
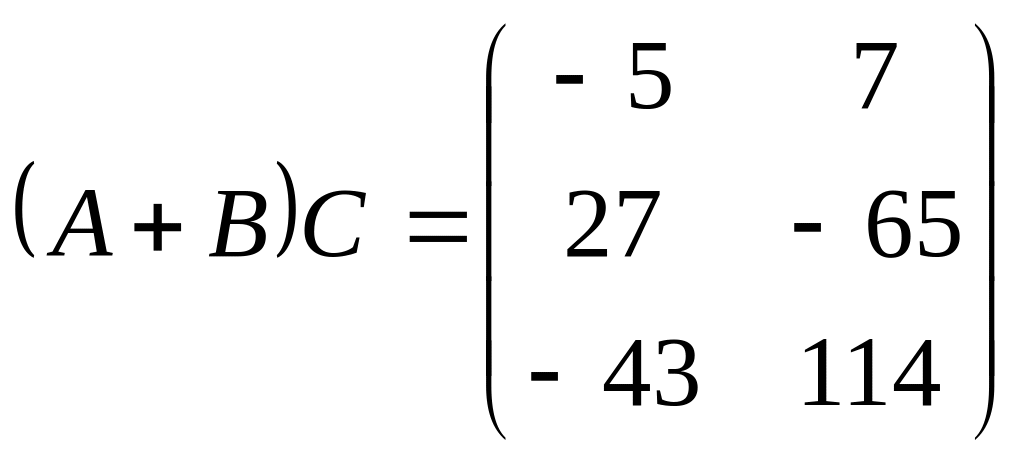 ,
,
![]() - не существует,
- не существует,
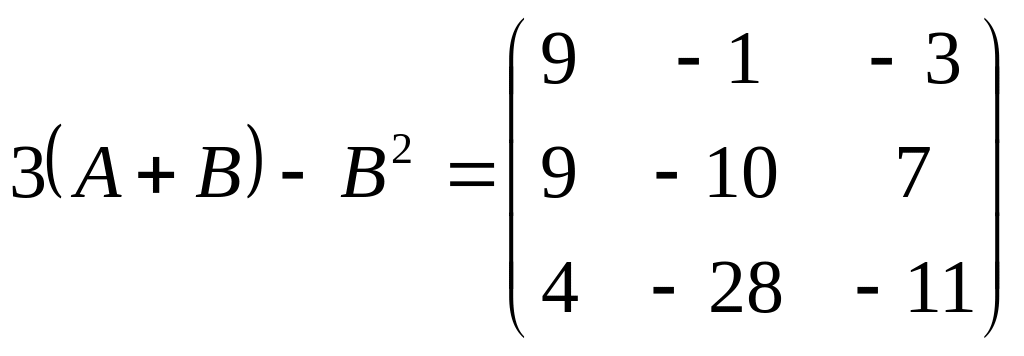 ,
,
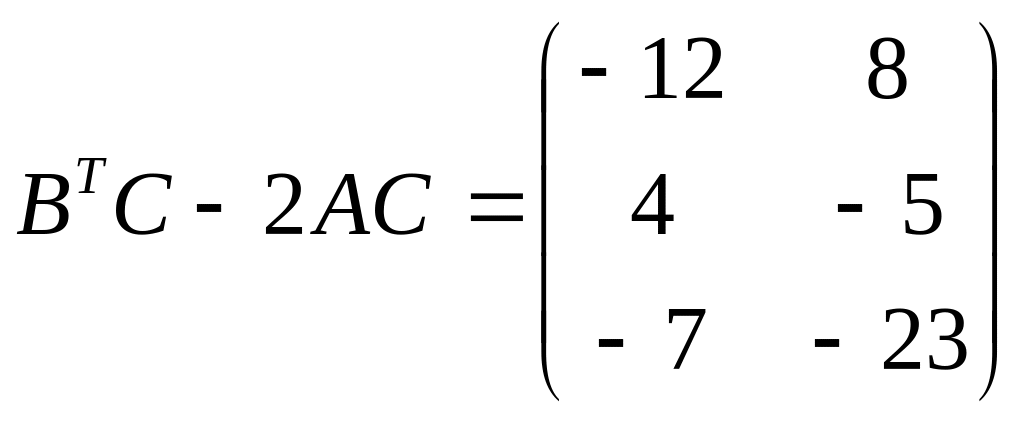 ;
;
6)
![]() ,
,
![]() - не существует,
- не существует,
![]() ,
,
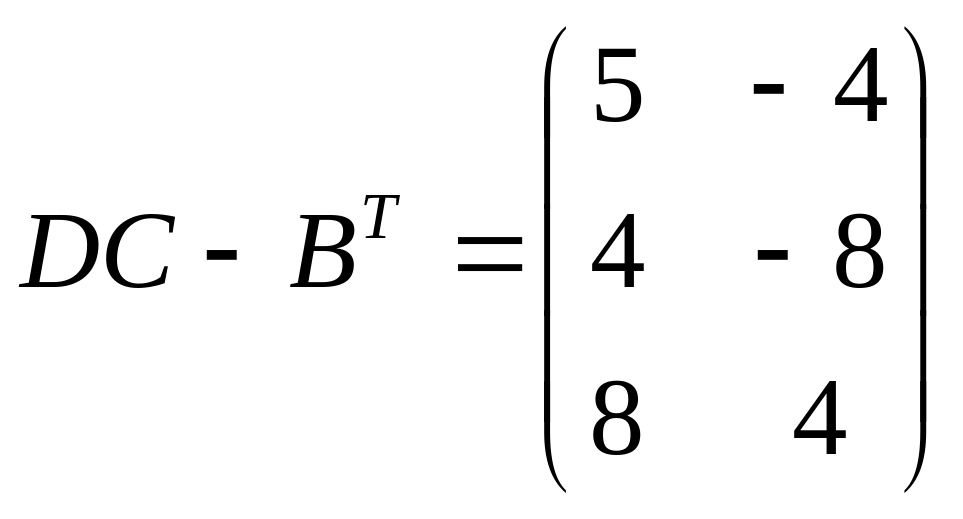 ,
,
![]() ,
,
 .
.
Домашнее задание.
Задания
7. Даны матрицы:
![]() ,
,
![]() ,
,
![]() .
.
Найти
матрицы
,
![]() ,
,
,
,
![]() ,
,
![]() ,
,
,
,
![]() ,
,
![]() если они существуют.
если они существуют.
Задания
8. Даны матрицы:
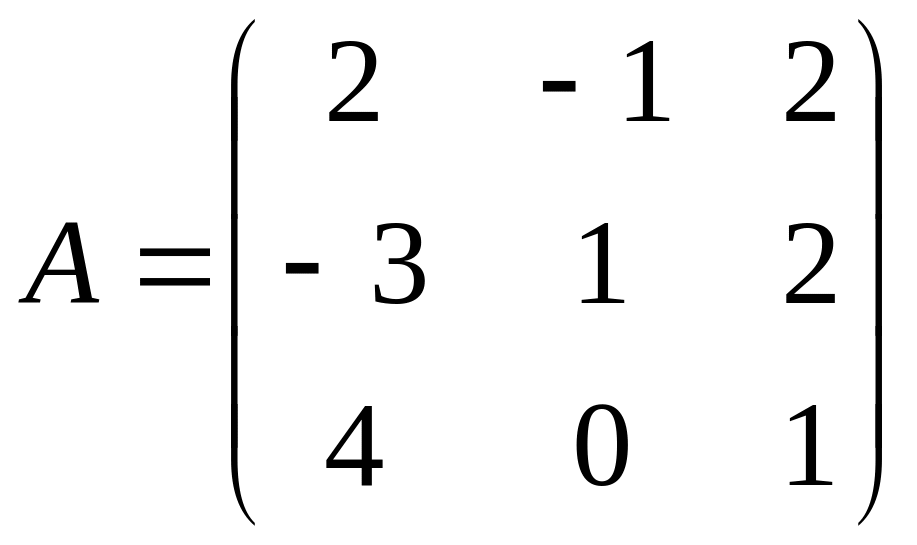 ,
,
![]() ,
,
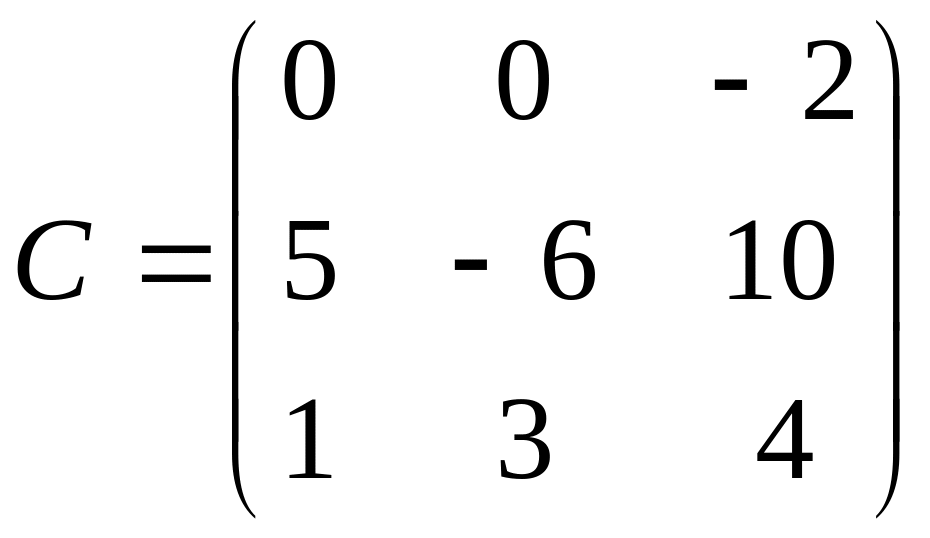
Найти матрицы, если они существуют |
1)
|
4)
|
|
2)
|
5)
|
|
3)
|
6)
|
Ответы:
7)
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
не существует,
-
не существует,
![]() ,
- не существует,
,
- не существует,
![]() ,
,
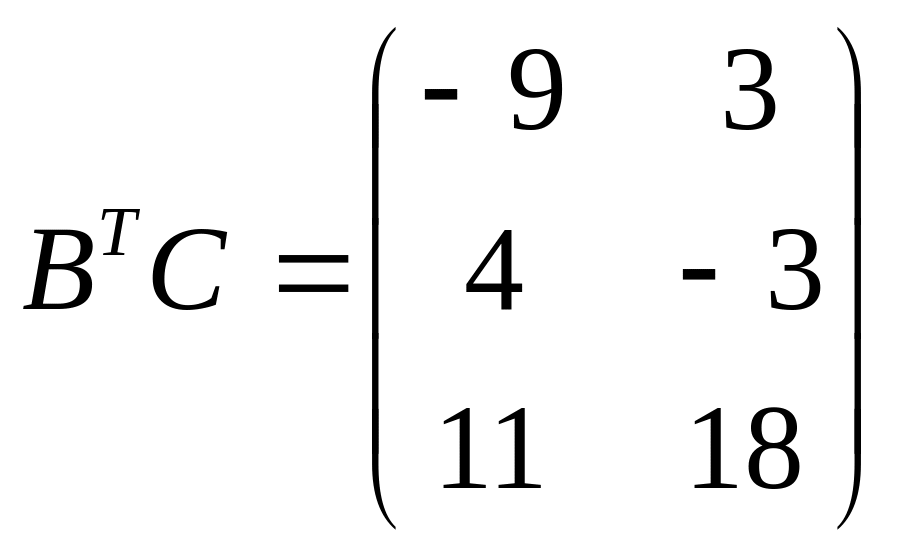 ;
;
8)
![]() ,
,
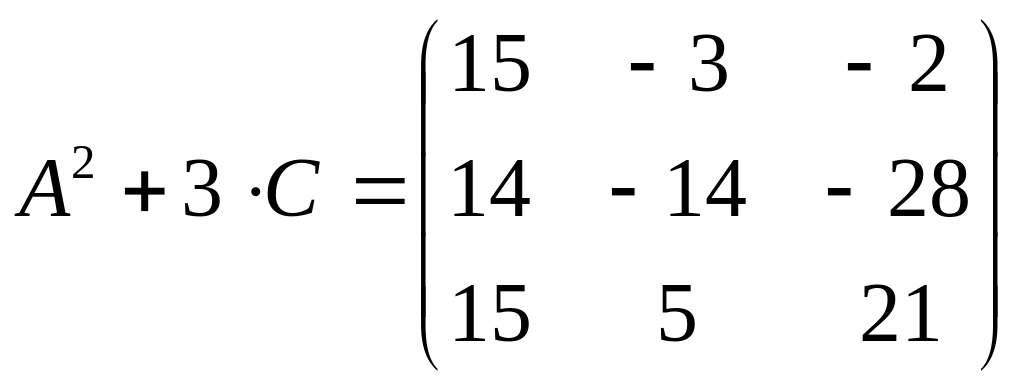 ,
,
![]() ,
,
![]() ,
,
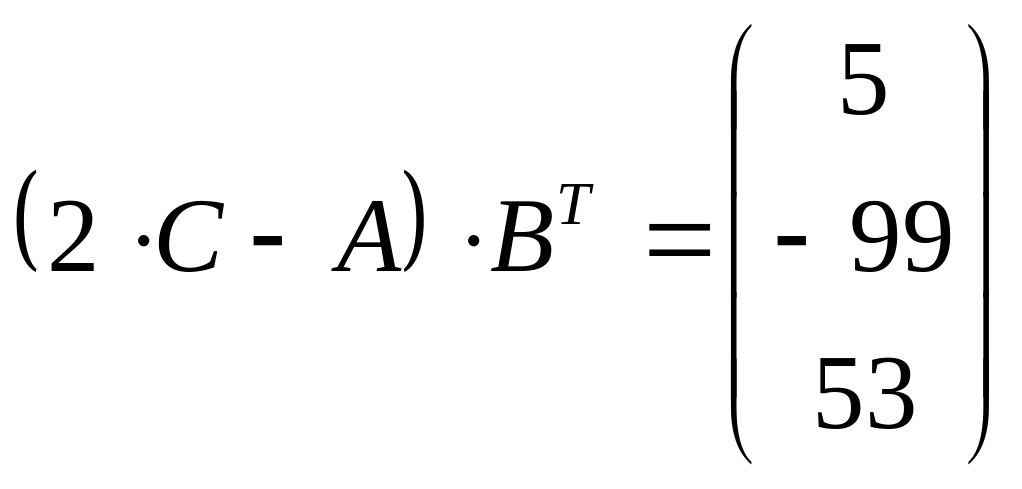 ,
,
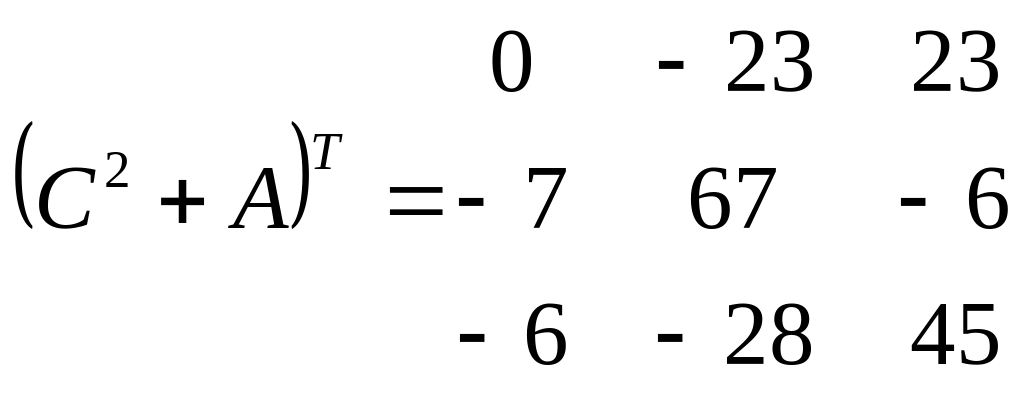 .
.
Определители. Формулы Крамера. Краткие теоретические сведения.
Определителем
квадратной матрицы первого порядка
![]() называется число
называется число
![]() .
(1)
.
(1)
Определителем
квадратной матрицы второго порядка
![]() называется число
называется число
![]() . (2)
. (2)
Определителем
квадратной матрицы третьего порядка
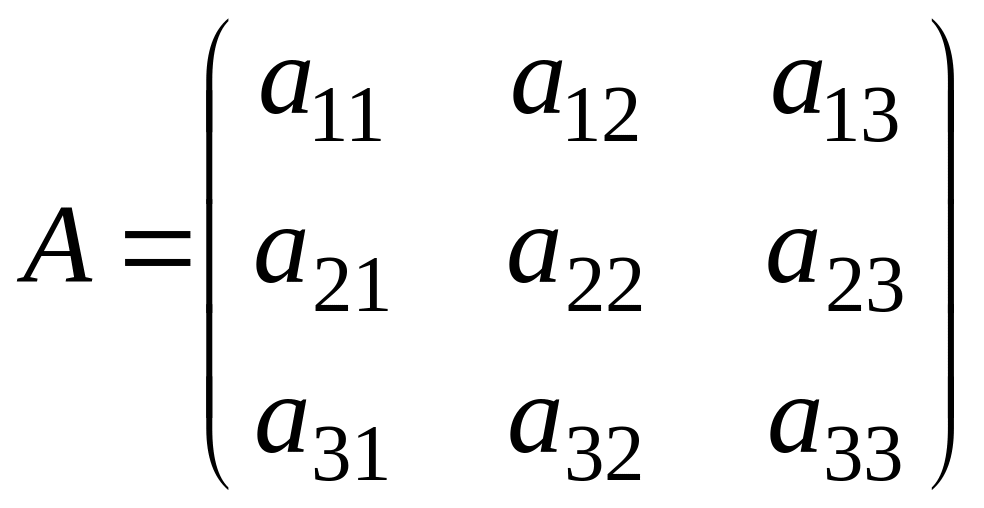 называется число
называется число
![]() (3)
(3)
Схема вычисления определителя третьего порядка
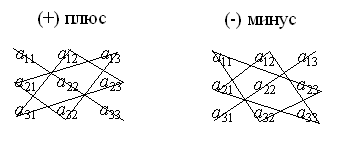
Некоторые свойства определителей.
1) Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен 0.
2)
![]()
3) Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.
4)
![]() .
.
Рассмотрим систему п линейных уравнений с п неизвестным
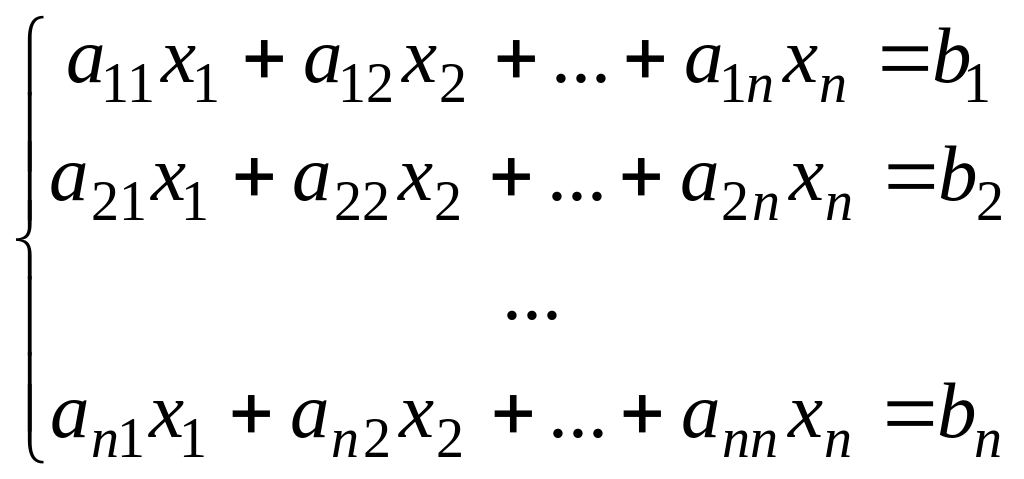 (4)
(4)
Определителем системы (4) называется определитель, составленный из коэффициентов при неизвестных:
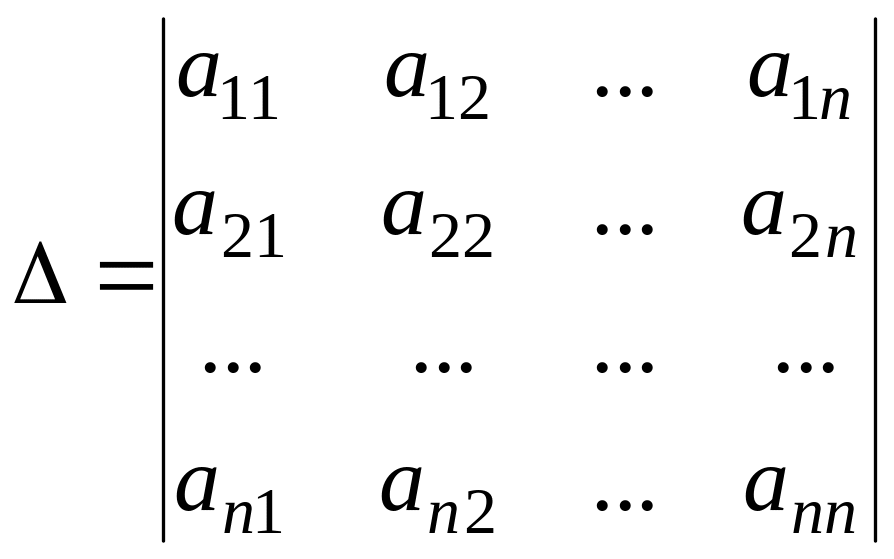 .
.
Обозначим
![]() - определитель, получающийся из
- определитель, получающийся из
![]() заменой k-го
столбца столбцом свободных членов
системы (4).
заменой k-го
столбца столбцом свободных членов
системы (4).
Теорема
Крамера.
Если
![]() ,
то система (4) имеет единственное решение,
определяемое по формулам:
,
то система (4) имеет единственное решение,
определяемое по формулам:
![]() (5)
(5)
Формулы (2) получили название формул Крамера.
Решение типовых заданий.
Задание 1. Вычислить определитель матрицы:
а)
![]() ,
б)
,
б)
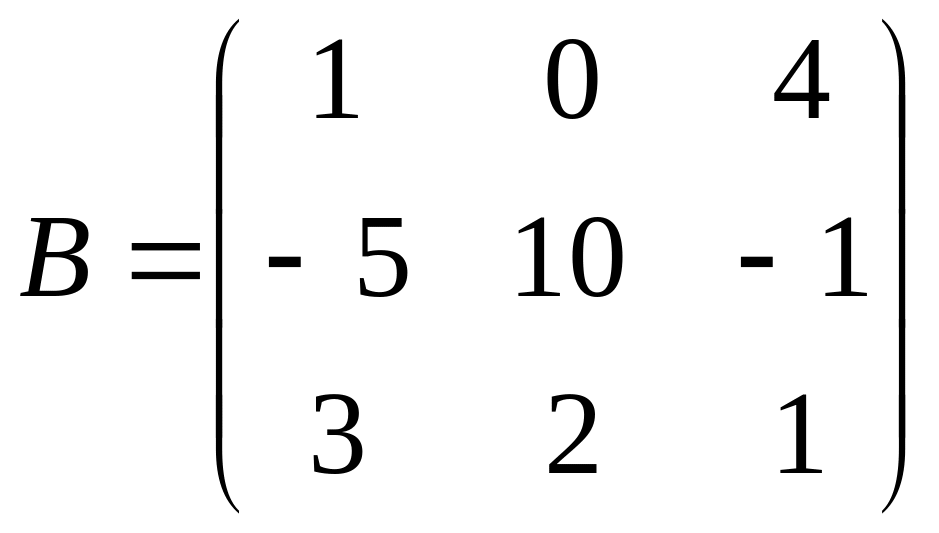 ,
в)
,
в)
![]() ,
г)
,
г)
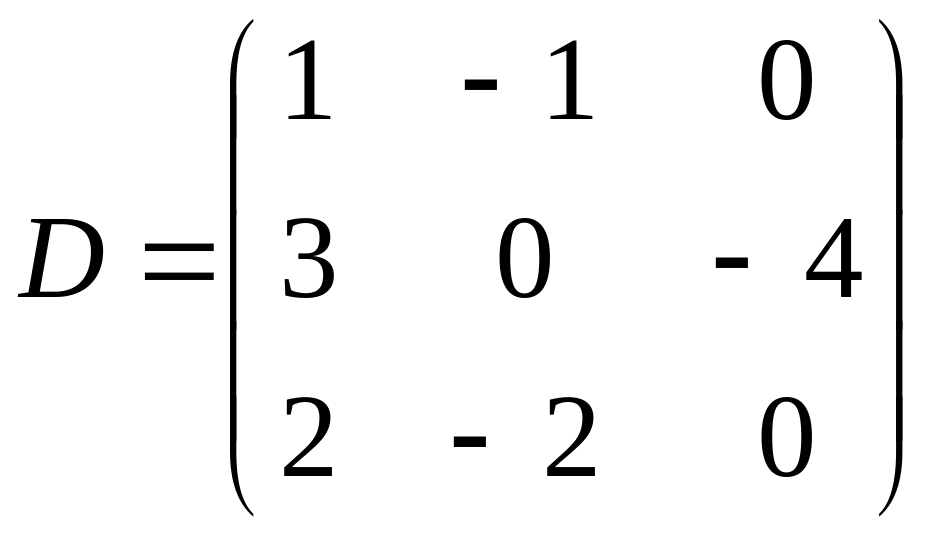 .
.
Решение:
а) Матрица A второго порядка, поэтому определитель находим по формуле (2):
![]() .
.
б) Матрица B третьего порядка, поэтому определитель находим по формуле (3):

в)
Матрица C
содержит столбец, состоящий из нулей,
поэтому по свойству 1):
![]() .
.
г)
Матрица D
содержит 2 строки (1-я и 3-я) с пропорциональными
элементами, поэтому по свойству 3):
![]() .
.
Задание 2. Решить систему уравнений по формулам Крамера:
![]() .
.
Решение:
Шаг 1: найти определитель системы
![]() .
.
Т.к. , то по теореме Крамера система имеет единственное решение
Шаг
2:
вычислить определители
![]() :
:
![]() .
.
![]() .
.
Шаг 3: по формулам Крамера (5) найти решение системы
![]() ,
, ![]() .
.
Шаг 4: сделать проверку, подставив полученные значения переменных в систему уравнений:
![]() ,
, ![]() .
.
