Решение типовых задач.
Задание
1. Упростите выражение:
.
Решение:
Шаг 1. Разложим знаменатель дробей на множители и приведем дроби к общему знаменателю.
.
Шаг 2. Раскроем скобки и приведем подобные.
.
Сократим числитель
и знаменатель на выражение
.
Получим
.
Ответ:
.
Задание 2. Найдите значение числового выражения:
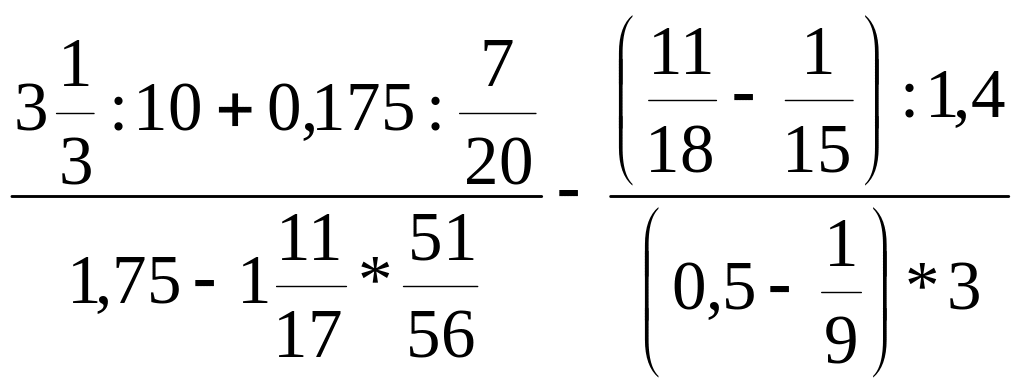
Решение:
Шаг 1. Определим порядок действий.
Шаг 2. Выполним действия:
1)
7)
2)
8)
3)
9)
4)
10)
5)
11)
6)
12)
Ответ: 3
Задания для самостоятельного решения.
Задание 3. Найдите значение числового выражения:
.
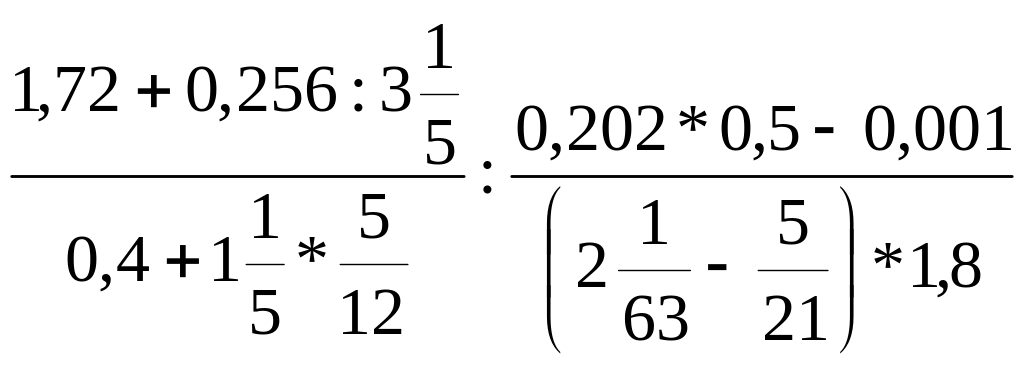Задание
4. Вычислите:
.
Задание
5. Упростите выражение:
.
Задание
6. Упростите выражение:
.
Задание
7. Упростите выражение и найдите его
значение при
.
.
Задание 8. Упростите алгебраическое выражение:
.
Задание
9. Упростите алгебраическое выражение:
.
Задание 10. Упростите алгебраическое выражение.
.
Ответы: 3) 64; 4) 1; 5)
;
6) 1; 7) 8; 8) 1; 9)
;
10)
.
Домашнее задание.
Задание
11. Найдите значение числового выражения:
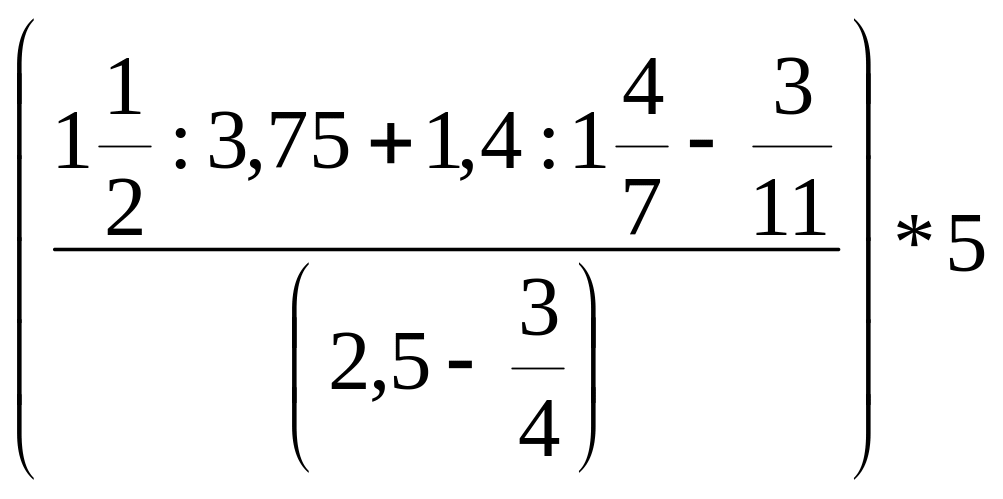
Задание
12. Вычислить:
.
Задание
13. Упростите:
.
Задание
14. Упростите выражение и найдите его
значение при
:
.
Задание
15. Упростите:
.
Задание
16. Упростите:
.
Ответы: 11) 40; 12)
8,1; 13)
;
14) 3; 15) 1; 16) 3.
Рациональные уравнения. Разложение на множители. Замена неизвестной.
Краткие теоретические сведения.
Уравнение вида
,
где
и
- многочлены, называется рациональным.
Пример 1:
.
При решении рациональных уравнений необходимо:
Обязательно учесть область определения уравнения.
Дробь превращается в ноль, когда числитель равен нулю
Решение типового задания.
Задание 1.
Решите уравнение
.
Решение:
Шаг 1. Найдем область определения уравнения.
Знаменатели дробей не равны нулю.
О.Д.З.:
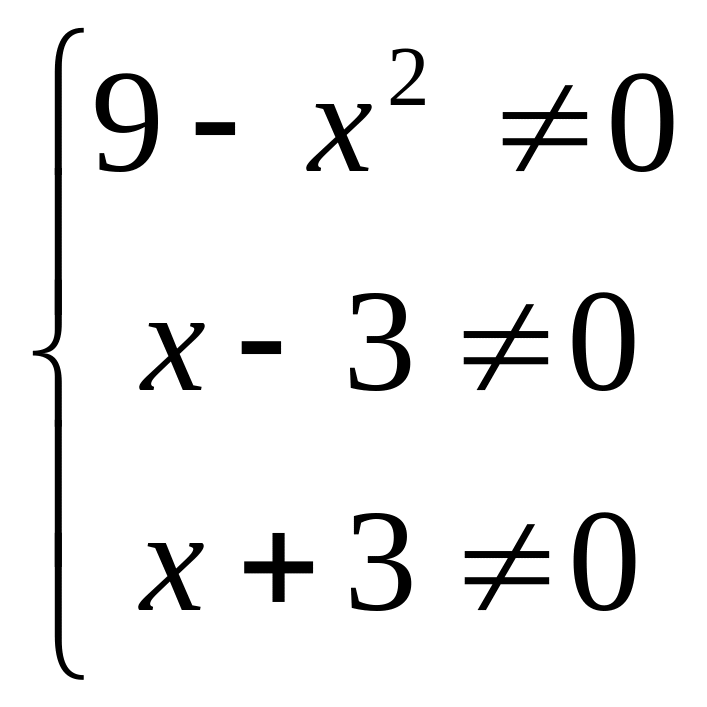
Шаг 2. Перенесем все дроби в левую часть равенства. Приведем дроби к общему знаменателю
.
Приведем подобные в числителе
.
.
.
или
- не входит в О.Д.З.
Ответ: .
Тождественное преобразование, приводящее к произведению нескольких множителей – многочленов или двучленов, называют разложением многочлена на множители.
Наиболее распространенные приемы разложение на множители:
Вынесение общего множителя за скобки.
Пример
2. Разложить на множители
.
Применение формул сокращенного умножения.
Пример
3. Разложить на множители многочлен
.
Решение: Используя формулы сокращенного умножения, получаем цепочку равенств
.
Применение выделение полного квадрата.
Суть этого приема состоит в выделении полного квадрата и последующего применения формулы разности квадратов.
Пример
4. Разложить на множители многочлен
.
Решение:
.
Способ группировки.
Суть этого приема состоит, в том, что все слагаемые многочлена группируются различными способами таким образом, чтобы в каждой группе после вынесения общего множителя за скобки, образовалось бы одно и тоже выражение. Это выражение также можно вынести за скобки как общий для всех групп множитель. Т.о. исходный многочлен окажется представленным в виде произведения.
Пример
5. Разложите на множители многочлен
Решение:
В первой группе
вынесем за скобки общий множитель
,
а во второй -
.
Получим
.
Теперь общий
множитель
также можно вынести за скобки
.
При решении уравнений можно использовать замену переменных, которая состоит в введении нового неизвестного. При его введении уравнение принимает более простой вид.
Пример 5:
Решите уравнение
.
Решение:
Введем новую
неизвестную
.
Тогда уравнение примет более простой
вид
.
Раскроем скобки
и решим квадратное уравнение относительно
переменной
.
или
.
Вернемся к неизвестной х.
или
или
или
.
корней нет.
Ответ:
,
.