Вычисление значений арифметических выражений. Краткие теоретические сведения.

Арифметическим (числовым) выражением называют математическое выражение, составленное из чисел, знаков арифметических действий и скобок.

Пример 1: 1) - числовое выражение.

2) - не числовое выражение, а бессмысленный набор символов.

Значением арифметического выражения называют число, которое получается при выполнении всех указанных в этом выражении действий, если их можно выполнить.

Если при нахождении значения арифметического выражения встречается деление на ноль, то говорят, что выражение не имеет смысла.

Пример 2. Вычислить значение числового выражения: .

Решение: Определяем порядок выполнения операций. Если нет скобок, то в первую очередь выполняются операции умножения и деления слева направо, а затем сложение и вычитание. Если есть скобки, то в первую очередь выполняются действия в скобках.

Выполняем операции с целыми числами в порядке действий:

1. 23-48=25

2. -25 : 5= - 5

3. -5 - 27=- - 32

4. -32 : (-8) = 4

5. 4 + (-16) = -12.

Ответ: Значение числового выражения -12.

Пример 3. Вычислить значение числового выражения:

((58-76):9+(-43)):(-5)+(-39)

Решение:

1. 58-76 = - 18

2. – 18 : 9 = - 2

3. – 2 + (- 43) = - 45

4. – 45 : (- 5) = 9

5. 9 +(- 39) = - 30

Ответ: - 30.

Пример 4. Найти значение: .

Решение:

1)

2)

3)

4)

Ответ: .

Задания для самостоятельного решения.

Задание 1. Вычислите .

Задание 2. Найдите значение выражения .

Задание 3. Вычислите .

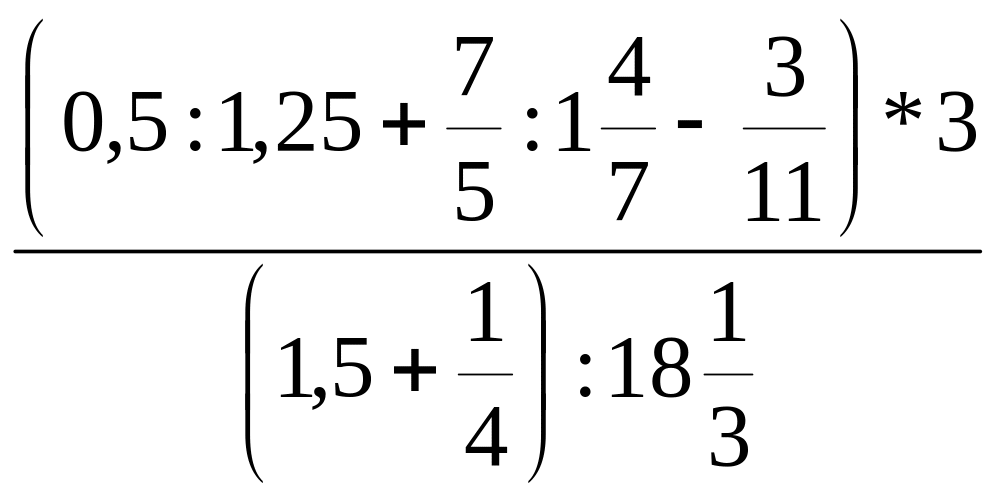Задание 4. Найдите х из пропорции: .

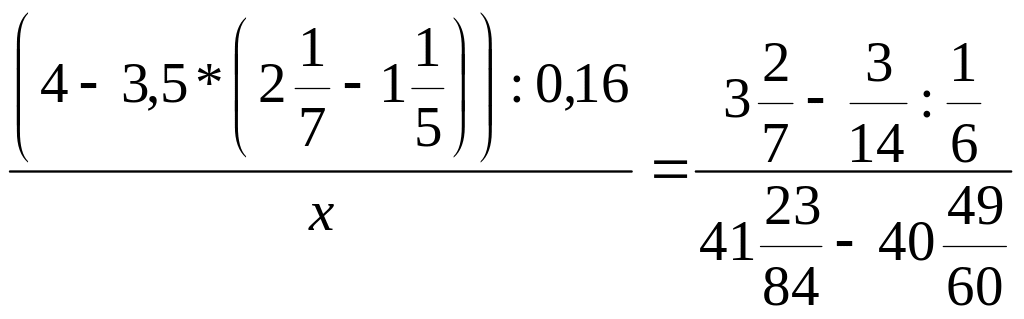Задание 5. Найдите х из пропорции: .

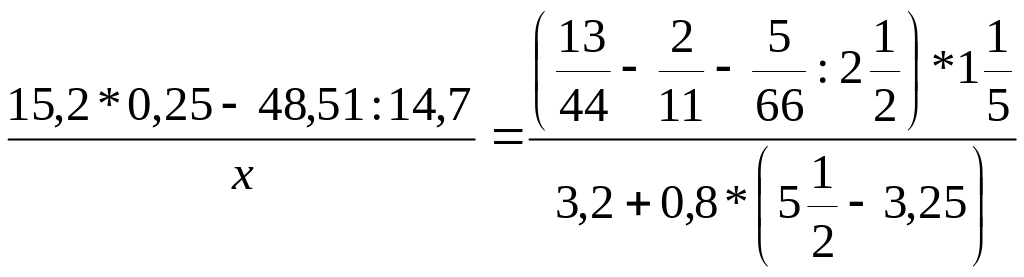Ответы: 1) 3; 2) 5; 3) 32.

Домашнее задание.

Задание 6. Вычислите: .

Задание 7. Вычислите: .

Задание 8. Вычислите: .

Задание 9. Вычислите: .

Ответы: 6) 1; 7) 3; 8) 2,5; 9) .

Линейные и квадратные уравнения и неравенства. Краткие теоретические сведения.

Линейное уравнение – это уравнение, содержащее неизвестные в первой степени и числа. Общий вид линейного уравнения с одной переменно: , где a и b – некоторые числа.

Решить уравнение – это значит найти все его корни или доказать, что корней нет. Сколько корней имеет линейное уравнение с одной переменной?

Если , то уравнение имеет единственный корень.

Пример 1.

.

Ответ: .

Если и , то уравнение имеет бесконечное множество корней.

Пример 2.

Ответ: x – любое число.

Если и , то уравнение не имеет корней.

Пример 3.

Ответ: корней нет.

Решение типовых задач.

Задание 1. Решите уравнение: .

Решение:

Шаг 1. Приведем дроби к общему знаменателю.

Общий знаменатель – 70.

Найдем дополнительные множители.

Шаг 2. Приравняем числители и раскроем скобки.

.

Шаг 3. Перенесем слагаемые, содержащие переменную x в левую часть равенства, а числа в правую.

Шаг 4. Приведем подобные и вычислим.

Ответ: .

Задания для самостоятельного решения.

Задание 2. Решить уравнение:

Задание 3. Решить уравнение:

Задание 4. Решить уравнение:

Ответы: 2) 3; 3) 1; 4) -0,25.

Уравнение вида , где х – переменная, a, b и с – некоторые действительные числа, причем , называется квадратным уравнением.

Для нахождения корней квадратного уравнения следует вычислить дискриминант .

Возможны три случая:

1. Если , то квадратное уравнение не имеет действительных корней.

2. Если , то корни совпадают и уравнение имеет единственное решение .

3. Если , то квадратное уравнение имеет два корня:

и .

Пример 1. Решить уравнение: .

Вычисляем дискриминант этого уравнения.

.

По формуле корней найдем два корня:

и .

Ответ: , .

Пример 2. Решить уравнение: .

Вычислим дискриминант.

.

Уравнение имеет единственное решение .

Ответ: .

Пример 3. Решить уравнение: .

Найдем дискриминант .

.

Ответ: корней нет.

Если один из коэффициентов b или c равен нулю, то квадратное уравнение называется неполным. В этом случае можно не вычислять дискриминант.

Если , а , то .

Пример 4. Решить уравнение

и .

Ответ: , .

Если , уравнение примет вид .

Пример 5. Решить уравнение

или .

Ответ: , .

Иногда бывает удобно воспользоваться теоремой Виета, которая утверждает, что если у квадратного уравнения есть корни и , то выполняются соотношения

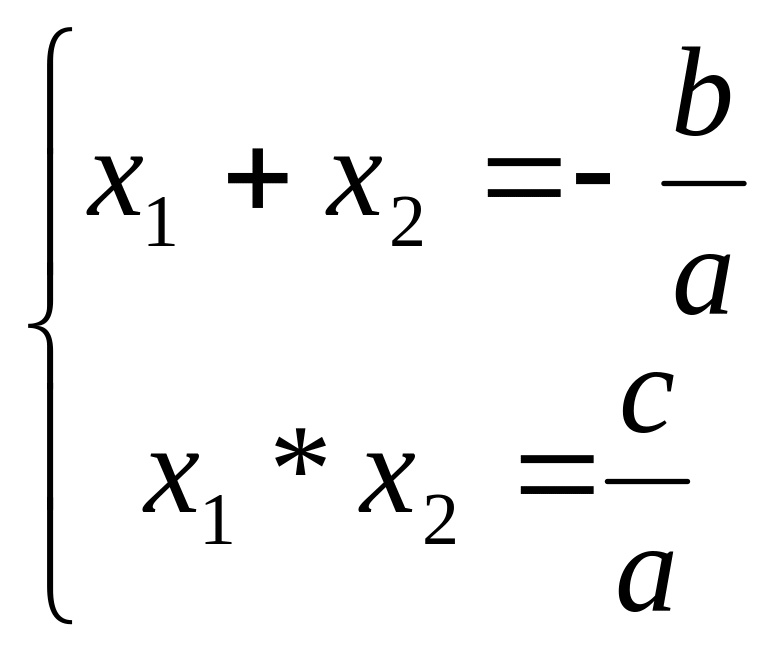
Пример 6. Решить уравнение .

Ответ: , .