Домашнее задание

Найдите значение производной в заданной точке.

24.19. , 24.20. , .

Вычислите производную функции.

24.21. 24.22.

24.23. 24.24.

Ответы

24.1. 2,5. 24.2. 24.3. 24.4. 24.5. 24.6. 24.7. 24.8.

24.9. 24.10. 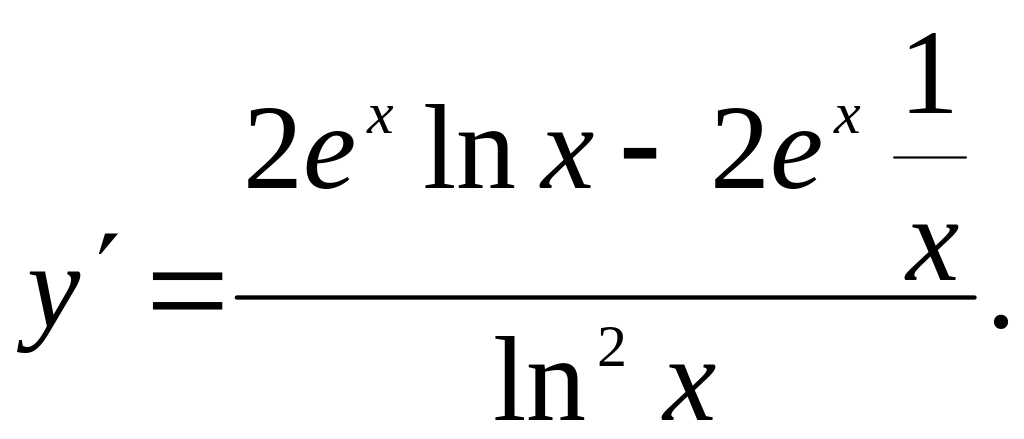24.11. 24.12. 24.13. 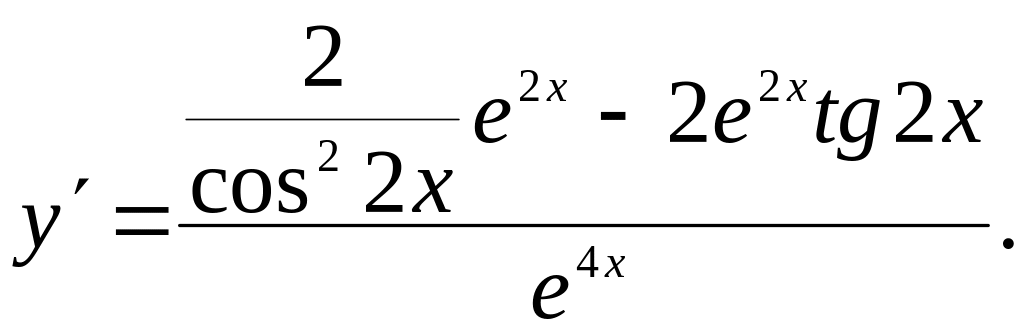24.14. 24.15 .

24.16.

24.17.

24.18. 24.19. 20. 24.20. 5. 24.21. 24.22. 24.23. 24.24.

25. Производная сложной функции Краткие теоретические сведения

Пусть y – сложная функция, т.е. , , или Если и – дифференцируемые функции своих аргументов соответственно в точках x и , то сложная функция также дифференцируема в точке x и ее производная находится по формуле .

Примеры решения типовых задач

Пример 1. Найдите производную функции .

Решение.

Находим производную заданной функции, применяя правила дифференцирования сложной функции, суммы и вынесения числового множителя за знак производной.

Шаг 1. Это сложная функция поэтому вначале находим производную от где : .

Шаг 2. Далее находим производную от подкоренной функции, которая представляет собой сумму двух слагаемых, при этом учитывая, что второе слагаемое также сложная функция: .

Шаг 3. Перемножаем полученные выражения и преобразовываем.

.

Итак, запись решения может выглядеть следующим образом:

Ответ:

Задания для самостоятельной работы

Найдите значение производной в заданной точке.

25.1. , . 25.2. ,

Найдите производные функций.

25.3. 25.4.

25.5. 25.6.

25.7. 25.8.

25.9. 25.10.

25.11. 25.12.

25.13. 25.14.

25.15. 25.16.

25.17. 25.18.

25.19. 25.20.

Домашнее задание

Найдите производные функций.

25.21. 25.22.

25.23. 25.24.

25.25. 25.26.

25.27. 25.28.

Ответ

25.1. 25.2. 25.3. 25.4. 25.5. 25.6. 25.7. 25.8. 25.9.

25.10. 25.11.

25.12. 25.13.

25.14. 25.15.

25.16.

25.17.

25.18. 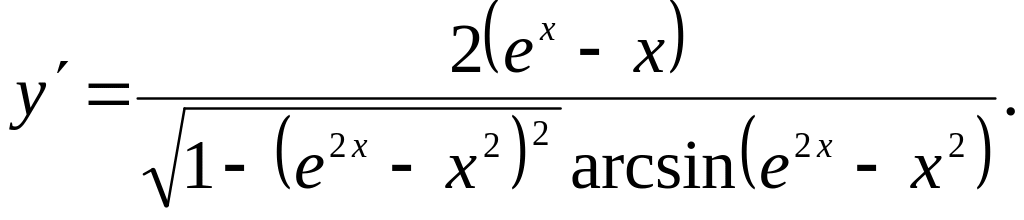25.19.

25.20. 25.21.

25.22. 25.23. 25.24.

25.25. 25.26.

25.27.

25.28.

26. Монотонность и экстремумы функции

Краткие теоретические сведения

Монотонной называется возрастающая или убывающая функция.

Теорема 1 (достаточное условие монотонности). Если функция дифференцируема на промежутке и ( ) для всех , то возрастает (убывает) на промежутке .

Точка называется точкой максимума (минимума) функции , если существует такая -окрестность точки , что для всех из этой окрестности выполняется неравенство ( ).

Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции.

Теорема 2 (необходимое условие экстремума). Если дифференцируема функция имеет экстремум в точке , то ее производная в этой точке равна нулю .

Точки, в которых производная дифференцируемой функции равна нулю, называются стационарными точками.

Точки, в которых производная дифференцируемой функции равна нулю или не существует, называются критическими точками.

Теорема 3 (достаточное условие экстремума). Если непрерывная функция дифференцируема в некоторой -окрестности критической точки и при переходе через нее (слева направо) производная меняет знак с плюса на минус, то – точка максимума функции; а если с минуса на плюс, то – точка минимума.

Если в некоторой проколотой окрестности точки производная имеет постоянный знак, то не является точкой экстремума.