Задания для самостоятельной работы
20.1. Какие из данных матриц могут иметь обратные?
,
,
,
.
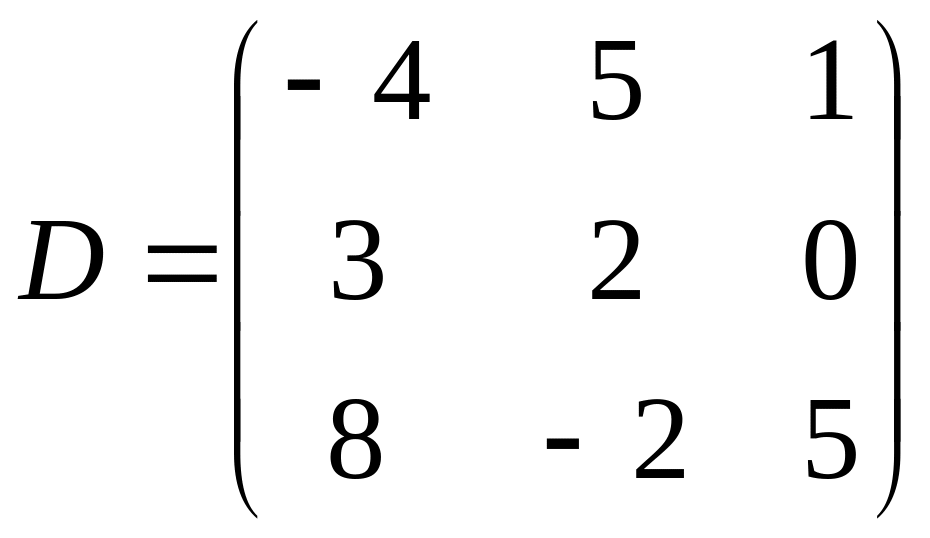20.2. При
каком значении
матрица
не имеет обратную матрицу?
20.3.
Найдите
алгебраические дополнения всех элементов
матрицы
.
20.4. Найдите
матрицу, обратную данной
.
Запишите алгоритм решения.
20.5. Найдите
матрицу, обратную данной
.
Сделайте проверку. Запишите алгоритм
решения.
20.6. Найдите
алгебраические дополнения элементов
первой строки матрицы
20.7. Найдите
матрицу, обратную данной
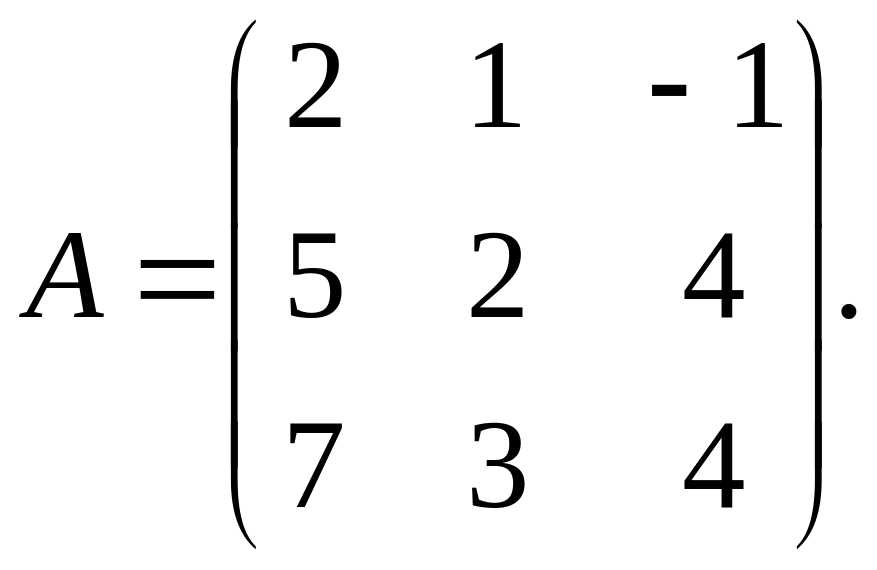Запишите алгоритм решения.
20.8. Найдите
матрицу, обратную данной
.
Сделайте проверку. Запишите алгоритм
решения.
20.9. Найдите
матрицу, обратную данной
.
Сделайте проверку. Запишите алгоритм
решения.
Домашнее задание
20.10. Найдите
матрицу, обратную данной
.
Сделайте проверку.
20.11. Найдите
матрицу, обратную данной
Сделайте проверку.
20.12. Найдите
матрицу, обратную данной
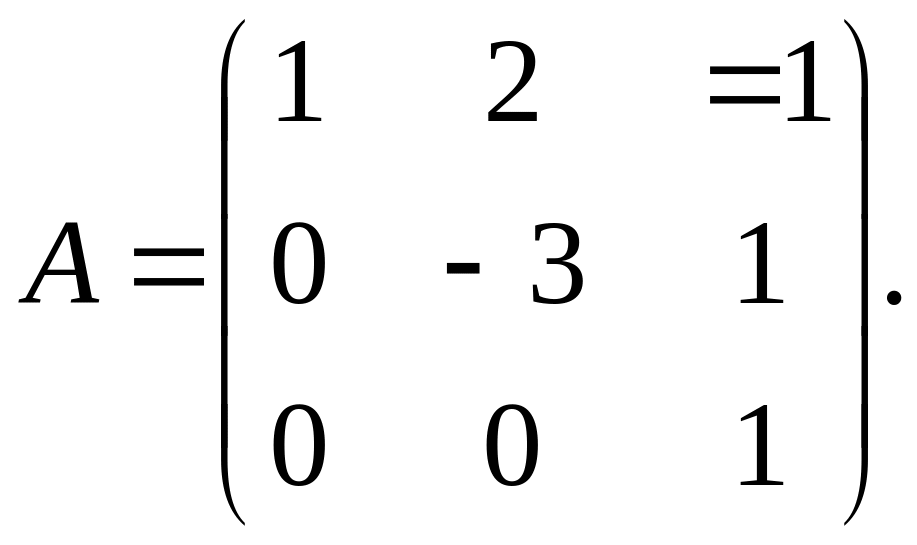Сделайте проверку.
Ответы
20.1. B,
D.
20.2.
20.3.
,
,
,
.
20.4.
20.5.
20.6.
,
,
.
20.7.
20.8.
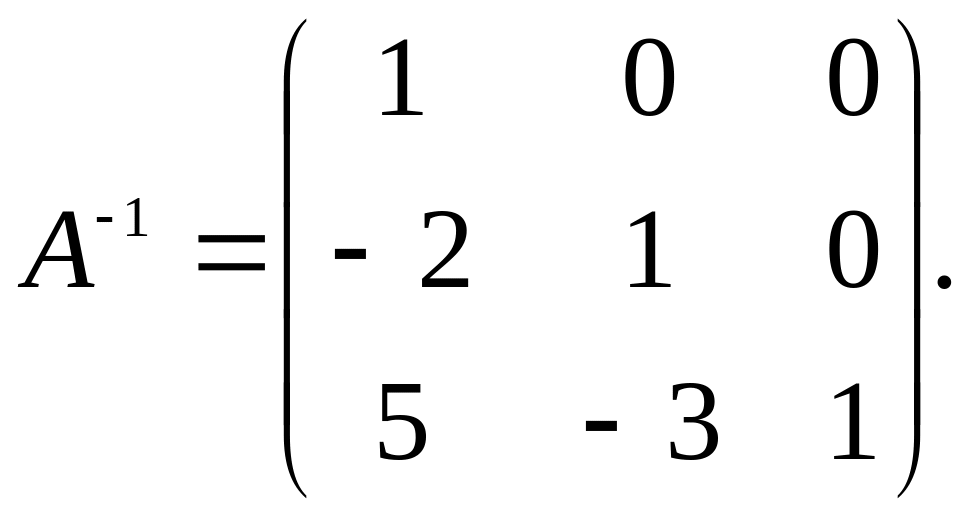
20.9.
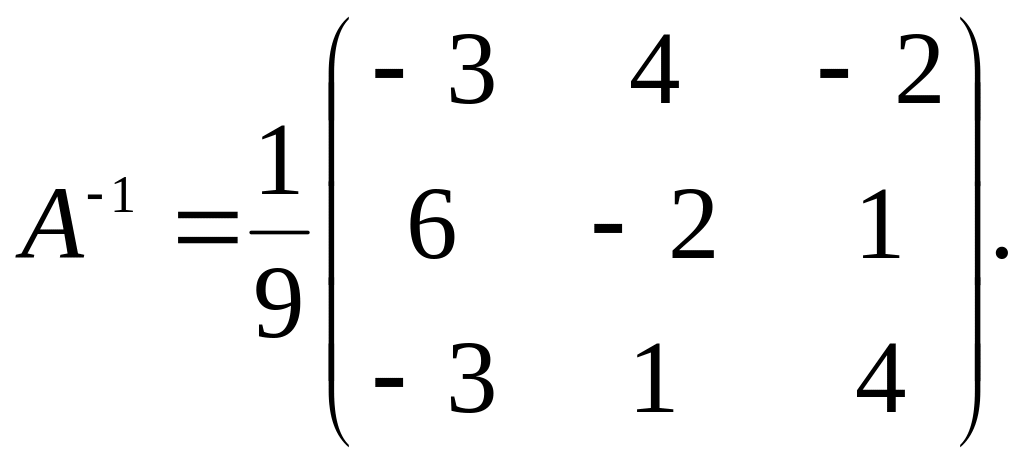20.10.
20.11.
20.12.
21. Системы линейных уравнений. Правило Крамера
Краткие теоретические сведения
Пусть дана система трех линейных уравнений с тремя неизвестными:
где
-
это неизвестные,
коэффициенты при неизвестных,
- свободные члены.
Матрица
,
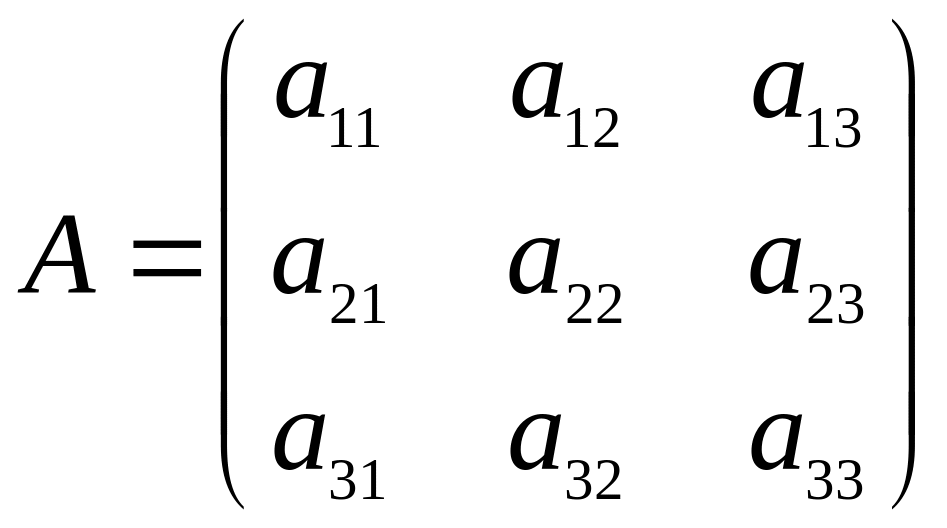состоящая из коэффициентов при
неизвестных, называется основной
матрицей системы, а определитель
называется определителем системы. Если
,
то система имеет единственное решение,
которое находят по формулам Крамера:
,
,
,
где
,
,
.
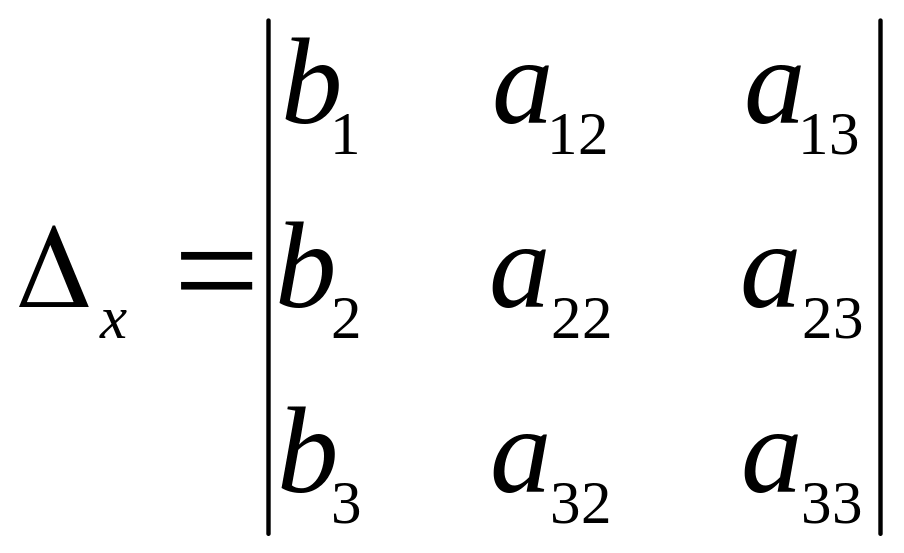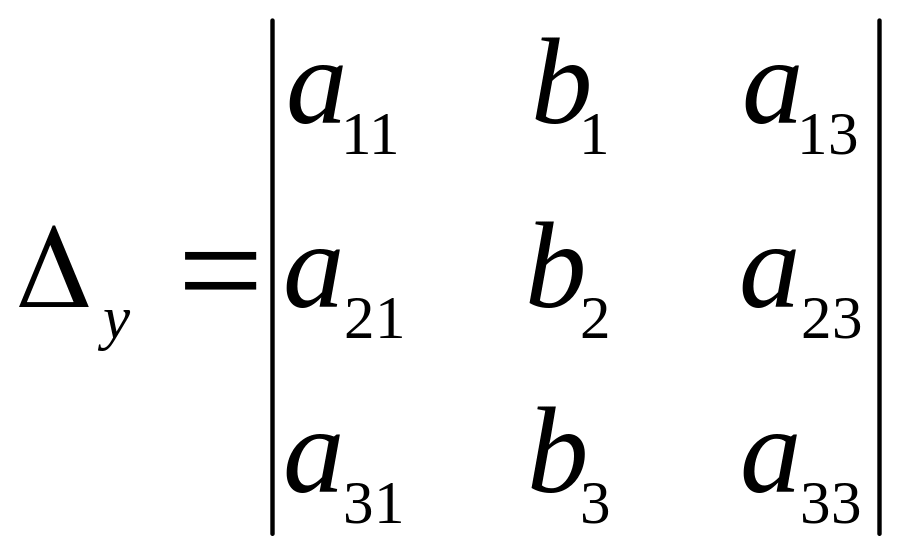Если
,
то правило Крамера не применимо, система
либо не имеет решений, либо имеет
бесконечное множество решений.
Если
система состоит из двух уравнений с
двумя неизвестными
,
то
,
,
.
Решение системы находим по формулам
Крамера:
,
.
Примеры решения типовых задач
Пример 1. Решите систему по правилу Крамера, сделайте проверку.
Решение.
Шаг 1. Вычисляем определитель , составленный из коэффициентов при неизвестных.
Этот определитель не равен нулю, значит, правило Крамера применимо и система имеет единственное решение.
Шаг 2.
Вычисляем определитель
.
Этот определитель получается из
заменой первого столбца столбцом
свободных членов, т.е. правых частей
уравнений.
Теперь можно
вычислить значение х:
.
Шаг 3.
Вычисляем определитель
.
Этот определитель получается из
заменой второго столбца столбцом правых
частей уравнений.
Вычисляем значение
y:
.
Шаг 4. Сделаем проверка. Подставим найденные значения х и у в уравнения системы.
Видим, что оба равенства верные, значит найденное решение верное.
Ответ:
,
.
Задания для самостоятельной работы
Решите систему по правилу Крамера, запишите алгоритм решения, сделайте проверку.
21.1.
21.2.
Решите систему по правилу Крамера, сделайте проверку.
21.3.
21.4.
21.5.
21.6.
21.7.
21.8.
21.9.
21.10.
Домашнее задание
Решить систему по правилу Крамера, сделать проверку.
21.11.
Решить систему по правилу Крамера.
21.12.
21.13.
Ответы
21.1.
,
21.2. Правило
Крамера применить нельзя.
21.3.
,
21.4.
,
21.5.
,
,
21.6.
,
,
21.7.
21.8.
,
21.9.
,
,
21.10.
,
21.11.
,
21.12. Правило
Крамера применить нельзя.
21.13.
,
22. Системы линейных уравнений. Метод Гаусса.
Краткие теоретические сведения
Системе линейных уравнений можно сопоставить матрицу, составленную из коэффициентов при неизвестных и правых частей уравнений:
Над такой матрицей можно выполнять три типа преобразований.
1. Менять строки местами.
2. Умножать строки на ненулевые числа.
3. Прибавлять к одной строке другую, умноженную на число.
Если в ходе преобразований получается строка, целиком состоящая из нулей, то такую строку можно вычеркнуть.
Целью преобразований является приведение матрицы к ступенчатому виду. Ступенчатой называется такая матрица, что каждая следующая строка содержит слева больше нулей, чем предыдущая.
Если в ступенчатой матрице есть строка, в которой до вертикальной черты стоят нули, а после вертикальной черты стоит ненулевое число, то система не имеет решения.
Если число строк в ступенчатой матрице равно числу неизвестных, то решение единственное. Чтобы найти это решение, нужно вычислять значения неизвестных, начиная с последнего уравнения, и подставлять найденные значения в предыдущие уравнения.
Если число строк в ступенчатой матрице меньше числа неизвестных, то решений бесконечное множество. В этом случае неизвестные нужно разделить на основные и свободные.
Затем нужно выразить основные неизвестные через свободные. Полученные таким образом выражения называются общим решением системы.
Такой метод решения систем линейных уравнений называют методом последовательного исключения неизвестных или методом Гаусса.