Примеры решения типовых задач
Пример 1.
Вычислить
интеграл
.
Решение.
Введём переменную
,
.
Тогда
.
Используем
формулу (1)
.
Ответ:
Пример 2.
Вычислить интеграл
.
Решение.
Положим
.
Тогда
.
Используя формулу (1), получим:
.
Ответ:
Пример 3.
Вычислить интеграл
.
Решение.
Положим
Тогда
и по формуле
интегрирования по частям получим:
.
Ответ.
Пример 4.
Вычислить интеграл
.
Решение.
Положим
Тогда
и по формуле
интегрирования по частям получим:
.
Ответ:
Задания для самостоятельной работы
Вычислите интегралы методом замены переменной.
31.1.
31.2.
31.3.
31.4.
31.5.
31.6.
31.7.
31.8.
Вычислите интегралы методом интегрирования по частям.
31.9.
31.10.
31.11.
31.12.
31.13.
31.14.
Домашнее задание
Вычислите интегралы методом замены переменной.
31.15.
31.16.
31.17.
Вычислите интегралы методом интегрирования по частям.
31.18.
31.19.
Ответы
31.1.
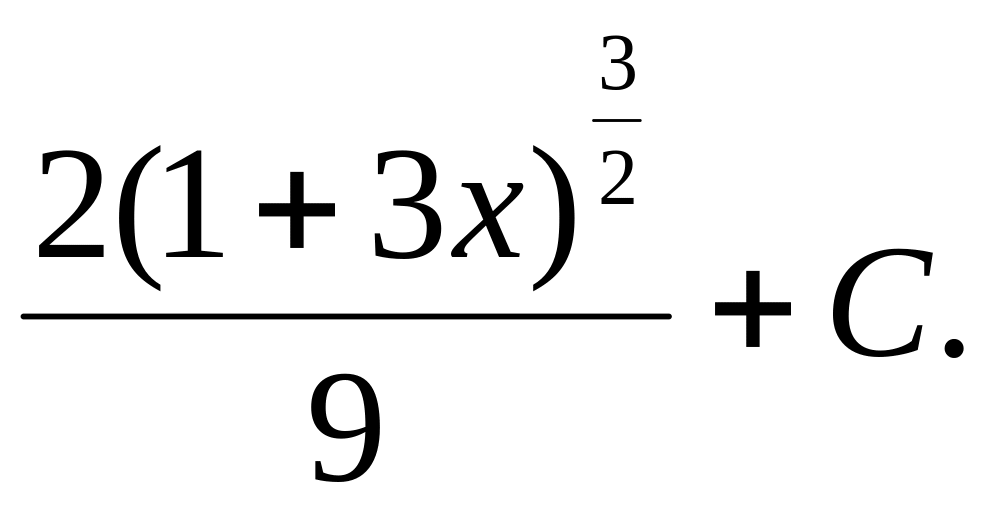31.2.
31.3.
31.4.
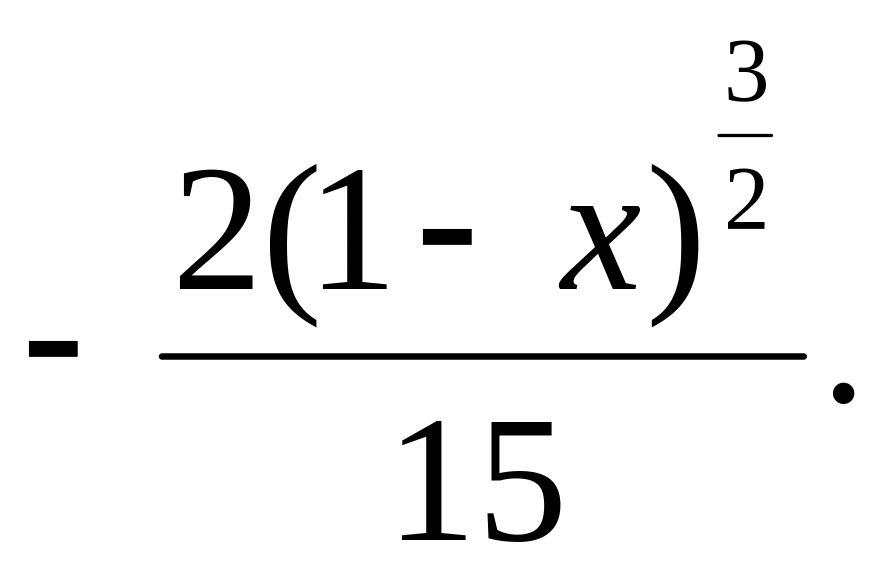31.5.
31.6.
31.7.
31.8.
31.9.
31.10.
31.11.
31.12.
31.13.
31.14.
31.15.
31.16.
31.17.
31.18.
31.19.
32. Вычисление определенных интегралов
Краткие теоретические сведения
Пусть функция интегрируема на отрезке
Теорема (Формула
Ньютона-Лейбница).
Если
– первообразная
функции
на
,
то
.
Теорема (замена переменной в определенном интеграле). Если
функция
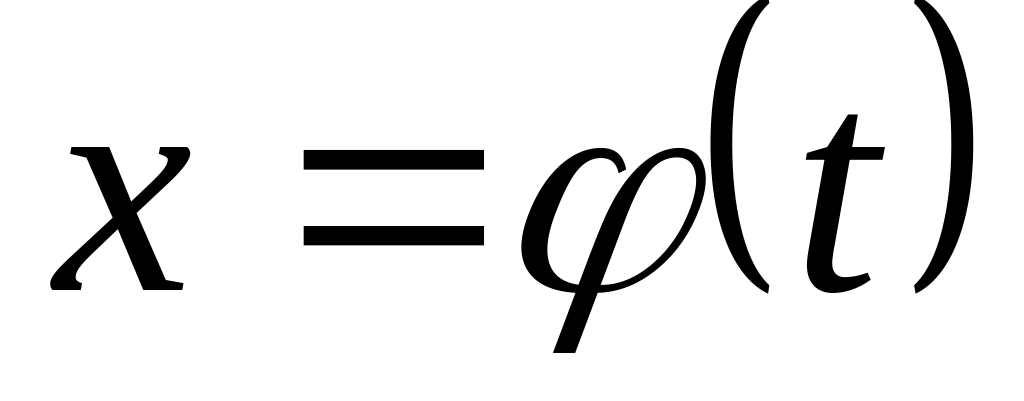и ее производная
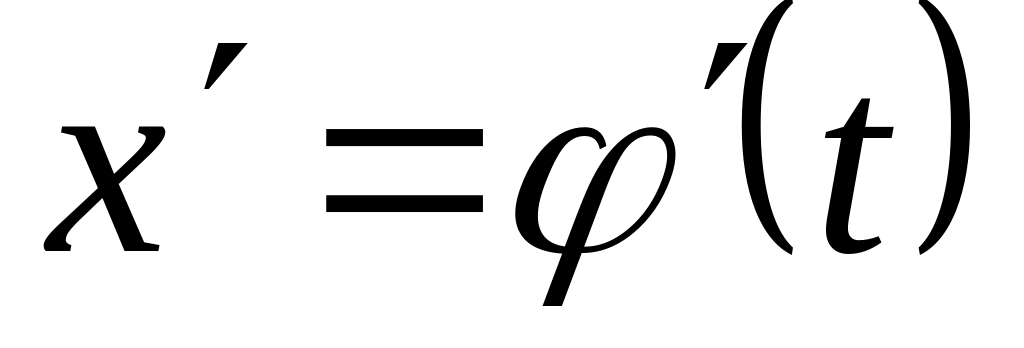непрерывны при
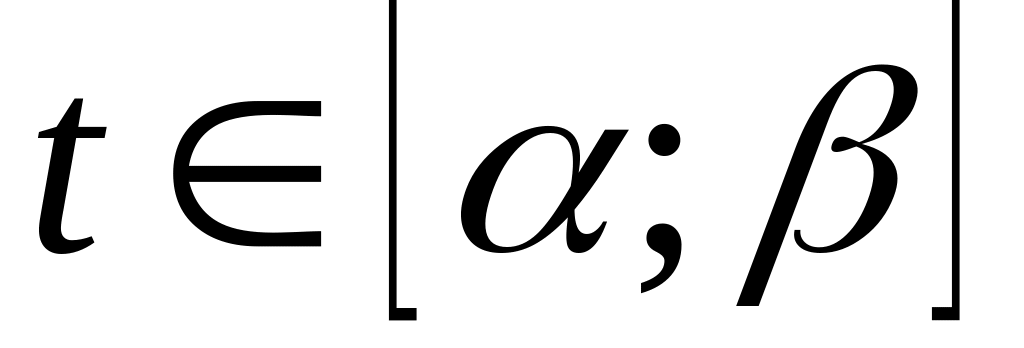;множеством значений функции при является отрезок
;
,
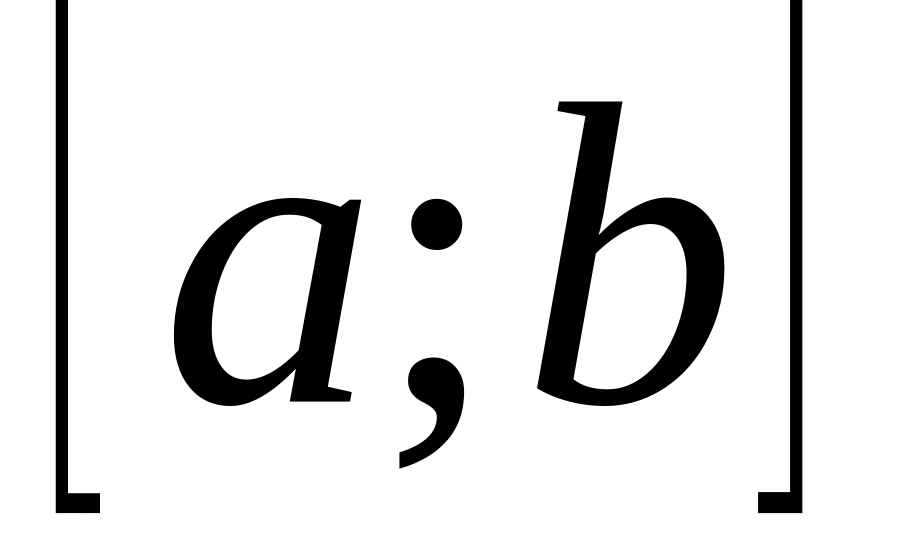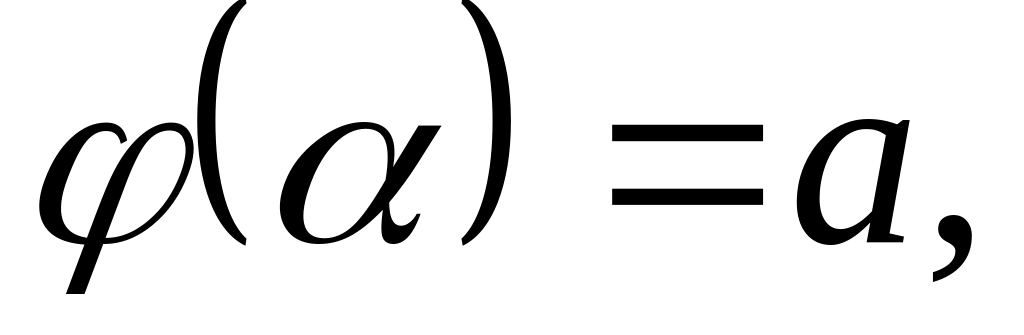
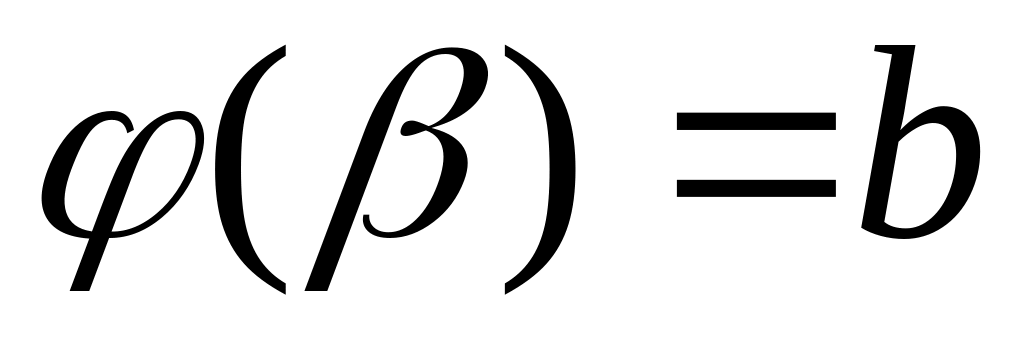то
.
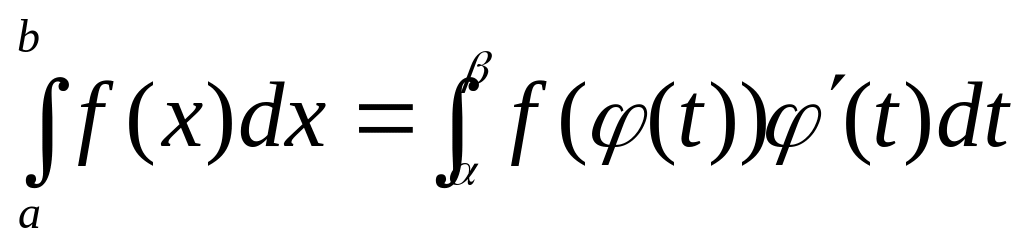Интегрирование
по частям в определенном интеграле
осуществляется с помощью формулы:
.
Некоторые свойства определенного интеграла
1.
При
перестановке пределов интегрирования
определённый интеграл меняет знак на
противоположный
.
2. Постоянный
множитель можно вынести за знак
определённого интеграла, т.е.
.
3. Определённый
интеграл от алгебраической суммы функций
равен алгебраической сумме их интегралов,
т.е.
.
Примеры решения типовых задач
Пример 1. Вычислить
определенный интеграл
.
Решение. Применяя свойство №3, разобьем интеграл на три интеграла:
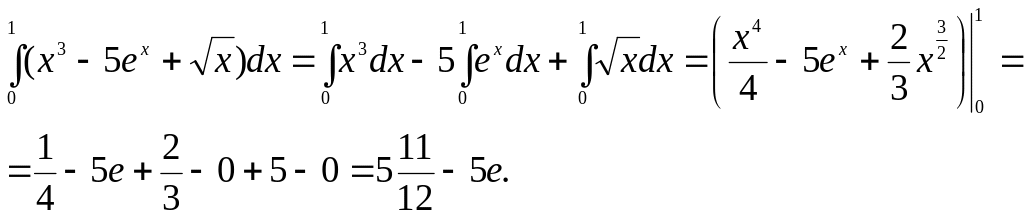
Ответ:
Пример 2.
Вычислить определенный интеграл
.
Решение. Положим
при
,
при
.
Применим подстановку
.
Ответ:
Пример 3.
Вычислить определенный интеграл
.
Решение. Применим
метод интегрирования по частям, пусть
.
Тогда
.
Ответ:
Задания для самостоятельной работы
32.1
32.2.
32.3.
32.4.
32.5.
32.6.
32.7.
32.8.
32.9.
32.10.
32.11.
32.12.
32.13.
32.14.
Домашнее задание
32.15.
32.16.
32.17.
32.18.
Ответы
32.1.
21.
32.2.
32.3. 1.
32.4.
0,21. 32.5.
0,33. 32.6.
32.7.
0,33. 32.8.
0,32.
32.9.
1,5.
32.10.
32.11.
0,57.
32.12.
4.
32.13.
0,25.
32.14.
32.15.
32.16. 0,67.
32.17.
32.18.
Список литературы
Высшая математика для экономистов: У Учебник для вузов/ Н.Ш.Кремер, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2004.
ГИА 2012. Математика: сборник заданий: 9 класс/ В.В. Кочагин, М.Н. Кочагина. – М.,2011.
ЕГЭ: 3000 задач с ответами по математике. Все задания группы В. Под ред. А.Л. Семенова, И.В. Ященко, – М., 2012.
ЕГЭ 2013. Математика. 30 вариантов типовых текстовых заданий и 800 заданий части 2 (С). Под ред. А.Л. Семенова, И.В. Ященко, – М., 2013.
Проскуряков И.В. Сборник задач по линейной алгебре. – М., 1984.