18. Определители Краткие теоретические сведения

Определитель – это некоторое число, поставленное в соответствие квадратной матрице. Пусть А – произвольная квадратная матрица порядка п. Определитель матрицы А будем обозначать .

Если п=1, то матрица А состоит из одного числа А. Положим по определению, что определитель такой матрицы равен числу А, т.е. .

Если п=2, то матрица А имеет вид . Определитель матрицы А вычисляется по формуле .

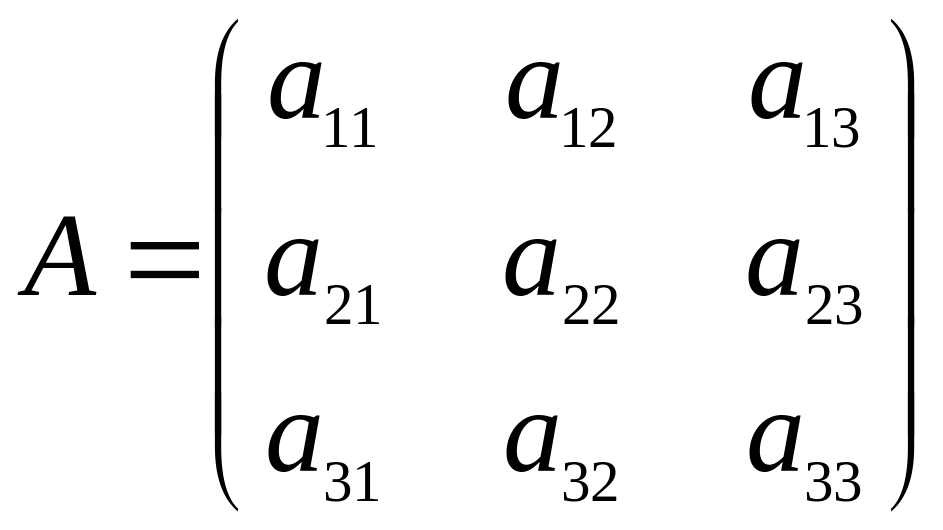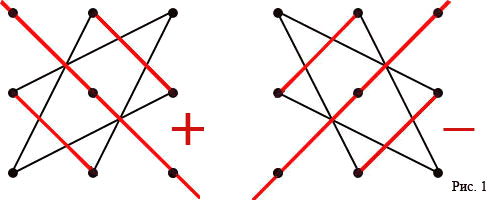
Если п=3, то матрица А имеет вид . Определитель матрицы А в этом случае вычисляется по правилу треугольников (рис. 1):

.

Теорема Лапласа: Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) матрицы на их алгебраические дополнения. Например, разложение определителя матрицы по первой строке имеет вид:

Основные свойства определителей

• Определитель не меняется при транспонировании матрицы.

• Определитель меняет знак, если поменять местами любые две строки (столбца) матрицы.

• Определитель матрицы равен нулю, если все элементы некоторой строки (столбца) равны нулю.

• Определитель матрицы равен нулю, если в этом определителе существуют две строки (два столбца), элементы которых пропорциональны, либо (в частном случае) равны.

• Определитель не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на число.

Примеры решения типовых задач

Пример 1. Вычислить определитель: .

Решение. Первый способ (по правилу треугольников): .

Второй способ (по теореме Лапласа):

Ответ: 10.

Пример 2. Вычислите определитель, приведя его к ступенчатому виду .

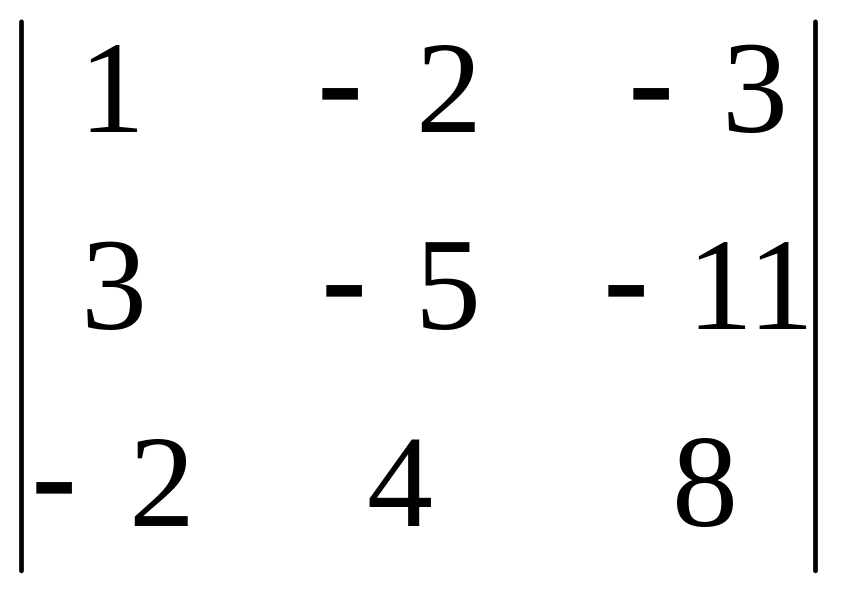Решение.

Шаг 1. Приведем определитель к ступенчатому виду.

Шаг 2. Определитель ступенчатого вида равен произведению диагональных элементов, значит определитель равен 2.

Ответ: 2.

Задания для самостоятельного решения

Вычислите определители.

18.1. 18.2.

18.3. 18.4.

Решите уравнения.

18.5. 18.6.

18.7. 18.8.

Вычислите определители по теореме Лапласа.

18.9. 18.10.

Вычислите определители, приведя их к ступенчатому виду.

18.11. 18.12.

18.13. 18.14.

Домашнее задание

Вычислите определители.

18.15. 18.16.

18.17. Решите уравнение

18.18. Вычислите определитель по теореме Лапласа

18.19. Вычислите определитель, приведя его к ступенчатому виду

Ответы

18.1. . 18.2. . 18.3. .18.4. . 18.5. 3. 18.6. 3. 18.7. 10. 18.8. 3. 18.9. 118. 18.10. 144. 18.11. 2. 18.12. 7. 18.13. 1. 18.14. 22. 18.15. 15. 18.16. 30. 18.17. 18.18. . 18.19. 3.

19. Сложение и умножение матриц

Краткие теоретические сведения

Суммой двух матриц и одинакового размера называется матрица размера такая, что (

Произведением матрицы размера на число называется матрица размера такая, что (

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением матрицы размера на матрицу размера называется матрица размера , каждый элемент которой равен сумме произведений элементов -й строки матрицы на соответствующие элементы -го столбца матрицы .