Индивидуальные задания (по бригадам)
По каждому варианту необходимо получить
аналитические выражения для
оптимального управления как функции
времени и оптимальные значения для
коэффициентов обратной связи, а также
построить графики переходных процессов
в оптимальной системе (
,
,
)
Для всех вариантов граничные значения
состояний объекта управления
.
Вариант (№ бригады) |
Объект управления |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
Приложение. Стандартные характеристические полиномы
Общая форма полиномов
(нормирование по базовой частоте
):
О динамических свойствах систем, имеющих рассматриваемые характеристические полиномы, можно судить по переходным характеристикам:
1. Биноминальные полиномы (Полиномы Ньютона)
Коэффициенты
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
2 |
1 |
2 |
1 |
|
|
|
|
|
|
3 |
1 |
3 |
3 |
1 |
|
|
|
|
|
4 |
1 |
4 |
6 |
4 |
1 |
|
|
|
|
5 |
1 |
5 |
10 |
10 |
5 |
1 |
|
|
|
6 |
1 |
6 |
15 |
20 |
15 |
6 |
1 |
|
|
7 |
1 |
7 |
21 |
35 |
35 |
21 |
7 |
1 |
|
8 |
1 |
8 |
28 |
56 |
70 |
56 |
28 |
8 |
1 |
Переходные характеристики
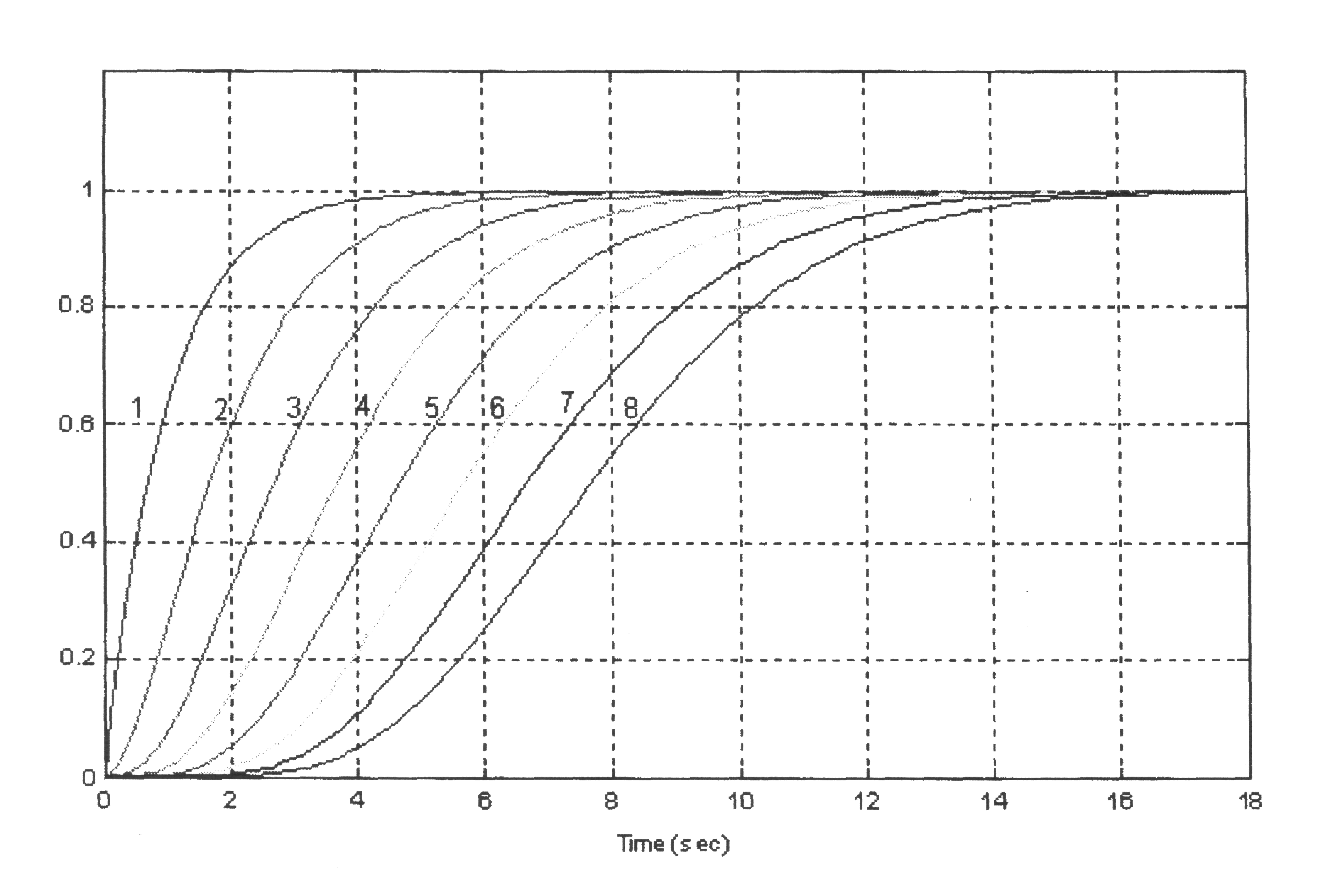
2. Полиномы Баттерворта Коэффициенты
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
2 |
1 |
1.4 |
1 |
|
|
|
|
|
|
3 |
1 |
2 |
2 |
1 |
|
|
|
|
|
4 |
1 |
2.6 |
3.4 |
2.6 |
1 |
|
|
|
|
5 |
1 |
3.24 |
5.24 |
5.24 |
3.24 |
1 |
|
|
|
6 |
1 |
3.86 |
7.46 |
9.13 |
7.46 |
3.86 |
1 |
|
|
7 |
1 |
4.5 |
10.1 |
14.6 |
14.6 |
10.1 |
4.5 |
1 |
|
8 |
1 |
5.12 |
13.14 |
21.84 |
25.69 |
21.84 |
13.14 |
5.12 |
1 |