4.4 Трассировка двумерных графиков

Для считывания значений координат точек из области графика необходимо, выделив график, нажать на кнопку панели инструментов Graph. В результате открывается окно (рис.4.5). После щелчка в области графика появляется графический курсор в виде перекрестия вертикальной и горизонтальной пунктирных линий, а в окне X-Y Trace отображаются значения координат точки, в которой находится перекрестие. Графический курсор можно свободно перемещать с помощь мыши в области графика, для перемещения курсора только вдоль линии графика должна быть установлена опция Track Data Points. Значения координат могут быть скопированы в буфер обмена (кнопки Copy X, Copy Y).

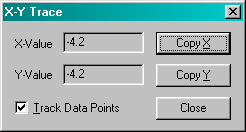
Рисунок 4.5 – Окно трассировки

Функция доступна для графиков в декартовой и полярной системах координат.

4.5 Изменение масштаба изображения

Для увеличения фрагментов графика следует, выделив его область, нажать на кнопку панели инструментов Graph. После ввода этой команды появляется окно

X-Y Zoom (рис. 4.6).

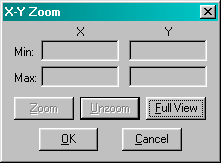
Рисунок 4.6 – Окно изменения масштаба

Фрагмент графика, который необходимо увеличить, следует выделить мышью и выбрать кнопку Zoom (Unzoom – отмена , Full View – восстановление первоначального вида графика).

4.6 Построение графиков функций двух переменных

В Mathcad возможно построение графиков функций двух переменных в прямоугольной (декартовой), сферической и цилиндрической системах координат. Рассмотрим, как в них задаются координаты точки.

В декартовой системе координат положение точки в пространстве задается тремя координатами (рис. 4.7): (x, y z). Для построения графика должна быть задана функция, описывающая закон изменения аппликаты .

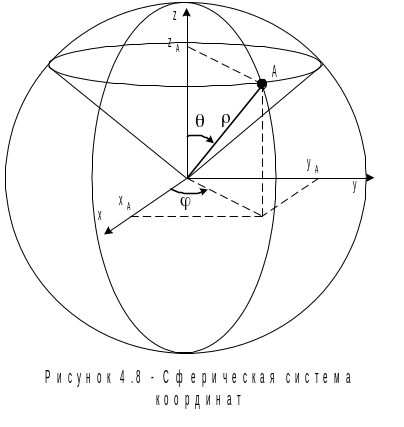
В сферической системе координат (рис. 4.8) положение точки задается радиусом , углами и . Для построения графика должна быть задана функция, описывающая закон изменения .

В цилиндрической системе координат (рис. 4.9) положение точки задается углом , радиусом и координатой . При построении графика в цилиндрической системе координат должна быть задана зависимость .

Для построения поверхности в выбранной системе координат необходимо:

1. Определить функцию двух переменных.

2. Выбрать вид графика, нажав одну из кнопок панели инструментов Graph: - в виде поверхности, образованной линиями сетки, - в виде линий уровня, - в виде прямоугольных параллелепипедов с одинаковыми основаниями, - в виде отдельных точек, принадлежащих его поверхности. Тип графика впоследствии может быть изменен на вкладке General диалогового окна 3-D Plot Format, которое вызывается командой Format/Graph/3D Plot или командой Format из контекстного меню, появляющегося при щелчке правой кнопкой мыши в области графика (или двойной щелчок мышью на области графика).

В ячейке под системой координат ввести имя функции, описывающей поверхность. По умолчанию график функции будет построен в декартовой системе координат. Для задания сферической или цилиндрической системы координат необходимо в диалоговом окне задания формата графика 3-D Plot Format задать на вкладке Quick Plot Data ( поле Coordinate System) желаемую систему координат (рис. 4.10): Cartesian (декартова), Spherical (сферичекая), Cylindrical (цилиндрическая).

Рисунок 4.10- Вкладка Quick Plot Data диалогового окна 3-D Plot Format

Например (рис. 4.11), функция в декартовой системе координат описывает плоскость, параллельную плоскости xy, в цилиндрической – цилиндр радиусом 10, в сферической – сферу радиусом 10.

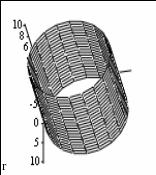
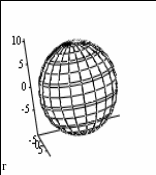
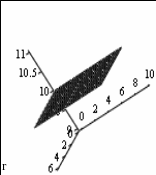
Рисунок 4.11 – Построение графика в цилиндрической, сферической и декартовой системах координат.

На рис. 4.12 приведен график функции в виде поверхности, линий уровня, отдельных точек, принадлежащих графику, прямоугольных параллелепипедов и др. Mathcad предоставляет большие возможности в области форматирования графиков (см. методические указания к лабораторным работам).

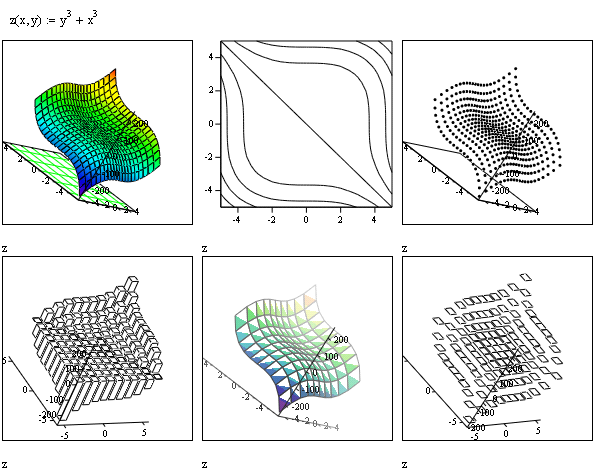
Рисунок 4.12 – Возможности форматирования графиков

Для построения графика функции двух переменных можно использовать предварительно созданную матрицу, каждый элемент которой равен аппликате поверхности. Для этого вместо имени функции следует ввести имя матрицы (рис.4.13).

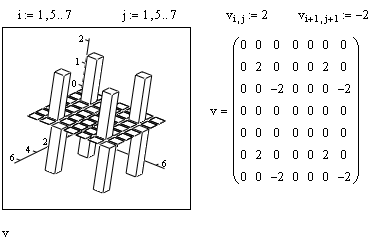
Рисунок 4.13- Использование значений элементов массива в качестве аппликат при построении трехмерного графика

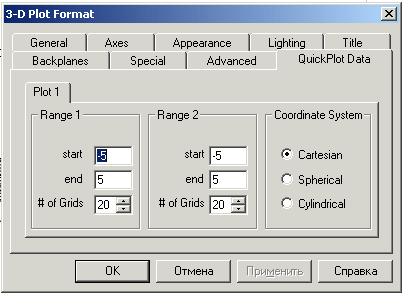
На вкладке Quick Plot Data диалогового окна 3-D Plot Format (рис. 4.10) могут быть введены начальное (start) и конечное (end) значения аргументов функции двух переменных и шаг их изменения (задается косвенно в поле # of Grids – число линий сетки). На рис. 4.14 график состоит из 8 фрагментов сферы, для каждого из которых соответствующим образом заданы начальное и конечное значение углов (Range 1) и (Range 2) (см. рис. 4.8).

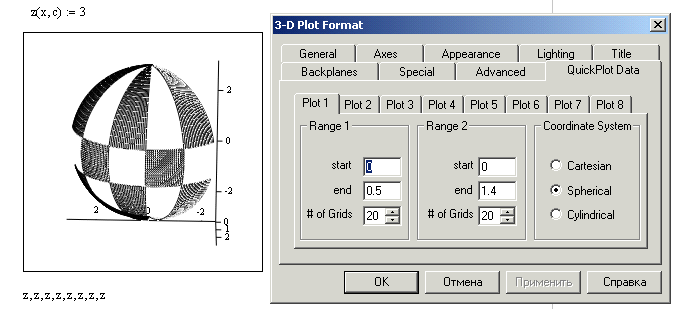
Рисунок 4.14 – Использование диалогового окна 3-D Plot Format для ввода начальных и конечных значений аргументов, выбора системы координат.

Для построения графика функции двух переменных, заданной параметрически, в ячейке под областью графика следует ввести в круглых скобках через запятую имена функций, задающих законы изменения их декартовых координат.

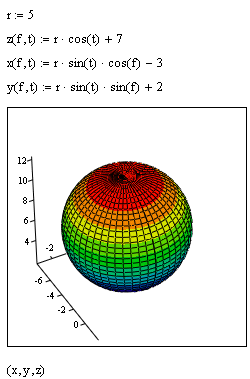
Например, как следует из рис. 4.8, параметрические уравнения сферы радиуса с центром в точке имеют вид: . Приведенные уравнения использованы при построении графика на рис. 4.15. Для поворота трехмерного графика следует переместить указатель мыши в область графика, нажать левую кнопку мыши, и, не отпуская, перемещать мышь в требуемом направлении. Поворот может быть выполнен и путем задания на вкладке General диалогового окна 3-D Plot Format углов поворота вокруг осей z (в поле Rotation) и x (в поле Tilt) или результирующего угла в поле Twist.

Рисунок 4.15 – построение графика функции, заданной параметрически.

Размер области любого графика может быть изменен. Для этого его необходимо выделить, переместить указатель мыши на черный маркер, расположенный на правой, нижней стороне рамки или в правом нижнем углу области графика, нажать левую кнопку мыши и, не отпуская, перемещать в нужном направлении.