
- •1.2 Структура документа Mathcad
- •1.3 Создание и редактирование документа Mathcad
- •2.1 Правила формирования идентификаторов
- •2.2 Управление режимом вычислений в Mathcad
- •2.3 Оператор присваивания. Локальные и глобальные переменные
- •2.4 Ввод и редактирование формул
- •2.5 Переменные, принимающие значения из заданного промежутка (ранжированные переменные)
- •2.6 Определение функций
- •Лекция 3
- •3.2 Ввод матриц
- •3.3. Панель инструментов Matrix. Действия над матрицами
- •4.2 Построение графиков в декартовой системе координат
- •4.3 Построение графиков в полярной системе координат
- •4.4 Трассировка двумерных графиков
- •4.5 Изменение масштаба изображения
- •4.6 Построение графиков функций двух переменных
- •4.7 Анимация
- •6.3 Вычисление определенного и неопределенного интеграла
- •6.4 Вычисление пределов
- •6.5 Вычисление суммы, произведения
- •7.1 Особенности выполнения символьных преобразований
- •7.2 Обзор символьных преобразований, выполняемых с помощью команд меню Symbolics
- •7.3 Панель инструментов Symbolic
- •7.4 Выполнение символьных преобразований
- •8.2 Решение алгебраических, трансцендентных уравнений с использованием команды Solve подменю Variable меню Symbolics
- •8.3 Решение неравенств
- •8.4 Применение функции root
- •8.5 Применение функции polyroots для определения корней полинома n-ной степени.
- •8.6 Использование функции lsolve для решения систем линейных уравнений
- •8.7 Использование директивы символьных преобразований solve для решения систем линейных и нелинейных уравнений
- •8.8 Применение блока решения систем линейных и нелинейных уравнений Given - Find (minerr) ( численное решение)
- •8.9 Применение блока решения для определения корней систем линейных и нелинейных уравнений в символьном виде
- •9.3 Примеры
- •Приложение а Перечень сообщений Mathcad об ошибках
- •Содержание
- •Список литературы
8.6 Использование функции lsolve для решения систем линейных уравнений
Для
решения системы линейных уравнений
вида
![]() ,
где
,
где
![]() - матрица коэффициентов,
- матрица коэффициентов,
![]() -
вектор корней,
-
вектор корней,
![]() - вектор свободных членов можно
использовать функцию lsolve:
- вектор свободных членов можно
использовать функцию lsolve:
lsolve(A, B).
Например:
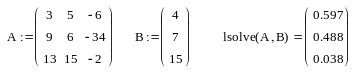
Другие способы решения системы линейных уравнений:
Путем нахождения матрицы, обратной матрице коэффициентов (
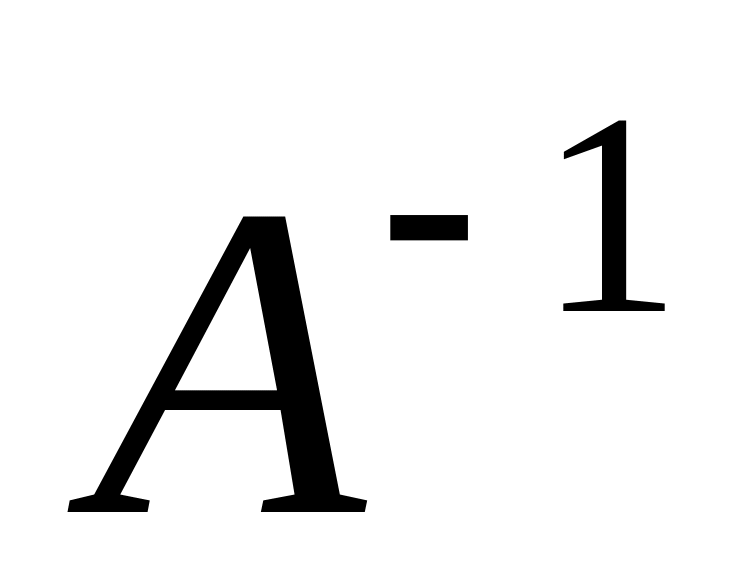 ):
):
 .
.Решение систем линейных и нелинейных уравнений в символьном виде с применением директивы символьных преобразований solve.
Использовать блок решения Given Find ( minerr) в символьном и численном виде.
8.7 Использование директивы символьных преобразований solve для решения систем линейных и нелинейных уравнений
Для получения символьного решения систем линейных или нелинейных уравнений с использованием директивы solve следует сформировать вектор, каждый элемент которого представляет собой одно из уравнений решаемой системы и применить директиву solve следующим образом:
![]()
Результат получается в виде матрицы, каждая строка которой представляет собой решение системы уравнений. Значения переменных в строках располагаются в порядке записи имен переменных за ключевым словом solve.
Пример 1. Решить систему линейных уравнений. |
|
Пример 2. Решить систему нелинейных уравнений в символьном виде |
|
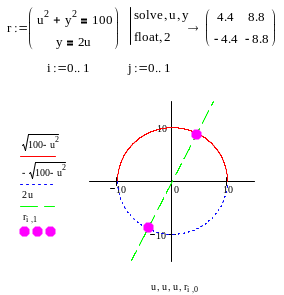
Пример 3. Решить систему нелинейных уравнений в символьном виде, результат представить в форме с плавающей точкой с двумя значащими цифрами. Проиллюстрировать найденное решение графически. |
|
8.8 Применение блока решения систем линейных и нелинейных уравнений Given - Find (minerr) ( численное решение)
Для решения уравнений или их систем можно использовать специальный вычислительный блок - блок решения.
Структура блока решения для численного определения корней:
Задание начальных приближений переменных - выполняется путем присваивания искомым переменным соответствующих значений.
<имя переменной 1>:=<значение переменной 1>
<имя переменной 2>:=<значение переменной 2>
…
<имя переменной n>:=<значение переменной n>
Начальные
приближения могут быть определены
графически, например, для системы из
двух уравнений
![]() начальными приближениями являются
координаты точек пересечения кривых
начальными приближениями являются
координаты точек пересечения кривых
![]() и
и
![]() на плоскости.
на плоскости.
Директива Given
Уравнения.
Ограничительные условия – задаются в виде неравенств (или равенств, которые должны выполняться для решений системы).
Выражение с одной из функций find, minerr в виде:
find(<имя перем. 1>,< имя перем 2>, …, < имя перем n>)
minerr(<имя перем. 1>,< имя перем 2>, …, < имя перем n>)
или в следующем виде:
<имя вектора решений>:= find(<имя перем. 1>,< имя перем 2>, …, < имя перем n>)
или
![]()
Примеры:
Решить систему линейных уравнений
с использованием блока решения. |
|
|
Дополнительно к предыдущему заданию сформировать вектор решения. |
|
|
Решить систему нелинейных уравнений
с использованием блока решения. Сформировать вектор решения. |
|
|
Блок решения может применяться и для решения одного уравнения.
|
|
|
Найти решение системы нелинейных уравнений
численными методами. Проиллюстрировать найденное решение графически. |
|
|
Найти численное решение системы уравнений ,
удовлетворяющее
дополнительному условию
|
|
|
В этом примере получаем тот же результат, применив функцию Minerr. В примере при задании исходной системы уравнений используются функции пользователя. |
|
|

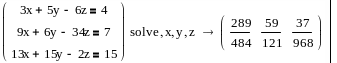




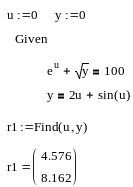
 или
или



