§7 Ряды фурье

Ортогонализация по Шмидту состоит в следующем.

Пусть дана система элементов h₁ ,h₂,…, образующих базис в евклидовом пространстве Н. Построим из этих элементах ортонормированную систему

e₁, e₂,…

Функция, принадлежащая пространству , раскладывается по системе ортогональных функций: в ряд

.

Коэффициенты Фурье вычисляются по формулам:

ЗАДАНИЕ 16

Применить процесс ортогонализации к базису пространства R³. Получить ортонормированный базис.

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

15. 

16. 

17. 

18. 

19. 

20. 

21. 

22. 

23. 

24. 

ЗАДАНИЕ 17

Разложить в ряд Фурье периодическую функцию с периодом Т= .

1) y= 2) y= 3) y=

4) y= 5) y= 6) y=

7) y= 8) y= 9) y=

10) y= 11) y= 12) y=

13) y= 14) y= 15) y=

16) y= 17) y= 18) y=

19) y= 20) y= 21) y=

22) y= 23) y= 24) y=

ЗАДАНИЕ 18

Разложить в ряд Фурье функцию.

1) 2)

3) 4)

5) 6)

7) 8)

9) 10)

11) 12)

13) 14)

15) 16)

17) 18)

19) 20)

21) 22)

23) 24)

ЗАДАНИЕ 19

Доопределяя необходимым образом заданную в промежутке функцию до периодической, получить для неё ряд Фурье

a) по косинусам; б) по синусам.

y

y 0 1 4

x

-1

2

1 -3

0 1 3 x

18.1 18.2

y y

0 1 4 х 0 1 4 х

-2

-3 -3

18.3 18.4

y y

0 1 2 4

х 1

0 3

-3 -1 1

-4 -2

18.5 18.6

y y

2

1

0 3 0 1 3

1 x -1 х

-2

18.7 18.8

y y

1 x x

0 0 2 3

-1 2 3

-2

18.9 18.10

y y

1 1

0 1 2 x 0 2 3 18.11 18.12

y y

2 2

0 2 4 х 0 2 4 х

18.13 18.14

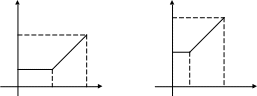y y

3 4

1 2

0 2 4 х 0 1 3 х

18.15 18.16

y y

2

0 2 4 5 х 0 1 3 4 х

-1 -1

18.17 18.18

y y

2

1

0 2 3 х 0 1 3 х

18.19 18.20

y y

2

1 1

0 1 3 x 0 2 3 x

18.21 18.22

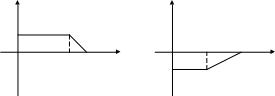y y

1

0 3 4 х 0 2 4 х

-1

18.23 18.24