Решение систем линейных уравнений.
1. Для решения систем линейных уравнений можно использовать и встроенную функцию lsolve(...).
Пусть задана система линейных уравнений:
В MathCad сначала записывается матрица коэффициентов и вектор правых часте имеют вид:
.
Затем записывается функция:
2. Матричный способ.
Система может быть представлена как A*X=B. Ищем ее решение матричным способом:
3. Решение систем линейных уравнений можно получать также при помощи блока Given ... Find(...).
Пример: решение системы линейных уравнений
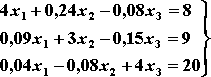
При нахождении корней полинома степени n лучше использовать функцию polyroots(v), где v – вектор длины n+1, содержащей коэффициенты полинома. Функция polyroots(v) возвращает сразу все корни полинома как вещественные, так и комплексные. Предварительно коэффициенты полинома должны быть представлены в в виде вектора (рис.6).
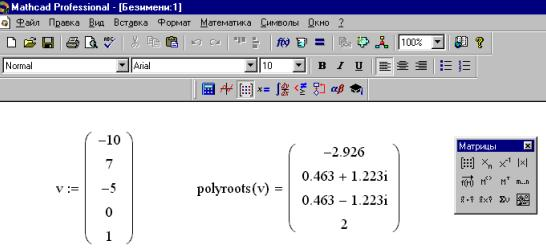
Рис. 6.
Задание 6.
Найдите решение системы линейных уравнений, соответствующей вашему варианту.
№ бригады |
Матрица коэффициентов системы |
Столбец свободных членов |
||
1 |
1.84 2.32 1.83 |
2.25 2.6 2.06 |
2.53 2.82 2.24 |
-6.09 -6.98 -5.52 |
2 |
2.18 2.17 3.15 |
2.44 2.31 3.22 |
2.49 1.49 3.17 |
-4.34 -3.91 -5.27 |
3 |
1.54 3.69 2.45 |
1.7 3.73 2.43 |
1.62 3.59 2.25 |
-1.97 -3.74 -2.26 |
4 |
1.53 2.35 3.83 |
1.61 2.31 3.73 |
1.43 2.07 3.45 |
-5.13 -3.69 -5.98 |
5 |
2.36 2.51 2.59 |
2.37 2.4 2.41 |
2.13 2.1 2.06 |
1.48 1.92 2.16 |
6 |
5 1 -3 |
0 3 2 |
1 -1 10 |
11 4 6 |
7 |
2 -1 1 |
0 3 -1 |
-1 1 4 |
-3 2 3 |
8 |
2 1 1 |
0 -3 1 |
-1 1 3 |
1 2 4 |
9 |
5 -1 1 |
1 3 -2 |
-1 1 4 |
-5 5 1 |
10 |
3 -2 1 |
1 4 1 |
-1 1 3 |
-1 5 -3 |