5 Проверка гипотезы о равенстве дисперсий. (оценка равноточности измерений)

5.1. Цель занятия

Практическое освоение правил сравнения двух дисперсий с помощью F-критерия Фишера, а также нескольких дисперсий с помощью критерия Бартлета и G-критерия Кохрена.

5.2. Сравнение двух дисперсий по критерию Фишера. Если, как это описано в примере 5.1 [1], известны объёмы выборок и их средние квадратические отклонения, то создавать электронную таблицу не надо. Сразу приступаем к процедуре сравнения дисперсий. Для этого последовательно щёлкаем левой кнопкой мыши по Compare (Сравнение) / Two Samples (Две выборки) / Hypothesis Tests (Тестирование гипотез) / OK.

В результате имеем таблицу (рис. 5.1), в которую вводим исходные данные из примера 5.1 [1] (СКО и объёмы выборок). Указываем, что сравнивать надо

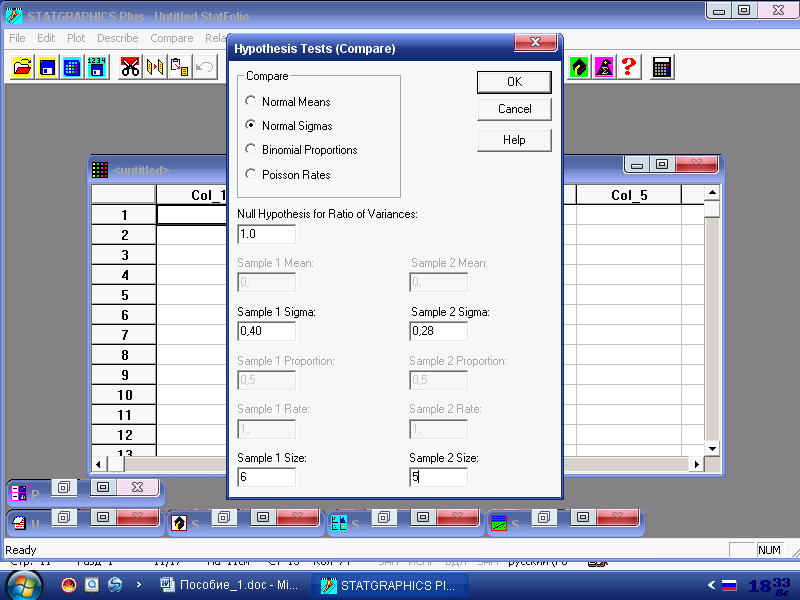
Рис. 5.1. Таблица для ввода исходных данных при сравнении равенства двух дисперсий по критерию Фишера

две дисперсии нормально распределённых совокупностей (Normal Sigmas), СКО (Sample 1 Sigma) и объём (Sample 1 Size) первой выборки, СКО (Sample 2 Sigma) и объём второй выборки (Sample 2 Size), далее ОК.

На рис. 5.2 представлены результаты тестирования.

Hypothesis Tests (Проверка гипотез)

----------------

Sample standard deviations (СКО выборок) = 0,4 and 0,28

Sample sizes (Размеры выборок) = 6 and 5

Null Hypothesis: ratio of variances = 1,0 (Нулевая гипотеза: отношение дисперсий равно 1)

Alternative (альтернативная гипотеза): not equal (дисперсии не равны)

Computed F statistic (Эмпирическое значение критерия Фишера) = 2,04082

P-Value (Вероятность принятия нулевой гипотезы)= 0,509247

Do not reject the null hypothesis for alpha = 0,05 (Нулевая гипотеза принимается для уровня значимости = 0,05).

Рис. 5.2. Результаты тестирования гипотезы о равенстве двух дисперсий по критерию Фишера

По результатам тестирования (последняя строка на рис.5.2) принимается нулевая гипотеза, правда, для близкого к критическому уровню значимости.

5.3. Сравнение нескольких дисперсий по критерию Бартлетта

и Кохрена

В тех вариантах примеров (5.2 и 5.3), как они представлены в [1], проверить гипотезы о равенстве дисперсий с помощью критериев Бартлетта и Кохрена в системе STATGRAPHICS Plus for Windows невозможно, так как в [1] в примерах представлены не выборки, между которыми необходимо проверить равноточность, а параметры этих выборок. Поэтому для решения этих задач в системе STATGRAPHICS Plus for Windows необходимо сначала создать электронную таблицу с тестируемыми выборками, а затем приступать к проверке равноточности измерений. Поскольку за давностью лет выборки из примеров 5.2 и 5.3 [1] были благополучно утеряны, то для иллюстрации применения критериев Бартлетта и Кохрена были смоделированы выборки с числом измерений, точно соответствующим примерам 5.2 и 5.3 [1] и с близкими к ним СКО.

RAND1 RAND2 RAND3 RAND4

10,0778 10,7624 14,3144 7,34189

9,37736 9,82844 11,6418 8,96278

9,95333 5,31757 27,0367 13,0175

9,77898 8,83633 1,17656 8,93481

11,6279 9,43949 0,82541 9,70829

6,96694 12,7772 8,99278 10,922

10,3927 11,8059 5,45325

9,95524 9,17322

9,1794 14,2146

Рис. 5.3. Модельные выборки «Бар» для проверки равенства дисперсий