2 Проверка годности первичных результатов измерений

2.1. Цель занятия

Практическое освоение правил оценки анормальности отдельных результатов измерений (промахов) и исключения их из выборки.

2.2. В настоящее время в специальной литературе по прикладной статистике описаны многочисленные приёмы проверки анормальности отдельных результатов измерений в выборке. В каждом конкретном случае использование того или иного критерия проверки определяется квалификацией и привычками оператора, моделью распределения случайных величин в выборке, объёмом выборки, используемым уровнем значимости и другими факторами. В практической метрологии наиболее часто используют правило или критерий «трёх сигм», смысл которого достаточно прозрачен и прост.

Если есть основания предполагать, что случайные величины (или их погрешности) в выборке распределены по нормальному закону, то вероятность попадания отдельных результатов за границы (x±3S) весьма мала, практически менее 0,002. Для технических измерений в металлофизике это очень маленькая величина, учитывая относительную погрешность технических измерений, обычно превосходящую 0,05. В случае генеральной совокупности это условие выглядит как (μ±3σ) откуда и вошел в практическую метрология термин «трёхсигмовый» интервал или «трёхсигмовый» критерий.

Таким образом, если «подозрительный» результат выходит за границы (x±3S), то его можно удалить из выборки и параметры выборки вновь определить по оставшимся значениям результатов измерений. Эту процедуру целесообразно проводить при удалении не более трети объёма выборки, в противном случае необходимо разобраться в причинах большого рассеяния результатов измерений. Причиной этого могут быть не только очевидные источники погрешностей (СИ, оператор, ошибки ввода данных и так далее), но и структурная (фазовая, химическая) неоднородность объекта измерений, что значительно интересней, так как дисперсия свойств в этом случае может служить инструментом исследования структурной (химической, фазовой) неоднородности объекта измерений.

В качестве примера рассмотрим результаты статистического анализа в предыдущем задании. Границы «трёх сигмового» интервала составят 422,06 и 478,52. Видно, что ни один исходный результат измерений (рис.1.1) не выходит за эти границы и, следовательно, можно считать, что аномальные результаты (промахи) в выборке отсутствуют. Этот вывод совпадает с результатом тестирования в примере 2.1 [1], хотя там использовался иной, непараметрический критерий проверки.

Система STATGRAPHICS Plus for Windows предоставляет, кроме того, исключительно простую и, главное, наглядную процедуру проверки анормальности результатов в выборке с помощью графиков Box-Whiskers («ящик с усами», рис. 1.3, правый нижний график). Правда, при этом предполагается, что результаты измерений распределены по нормальному закону.

Идея проверки анормальности заключается в следующем. Предполагается, что внутри «ящика» содержится 50 % данных. Вертикальная линия, разделяющая бокс на две части, соответствует медиане выборки. Остальные 50 % объёма выборки располагаются внутри усов. (Предполагается, что эти 100 % результатов распределены по нормальному закону с параметрами, оценки которых сделаны по выборке). Всё, что находится за границами усов, рассматривается как аномальный результат и может быть удалено из выборки. Количество таких точек характеризует степень «засорённости» выборки, которая отражает в определённой степени качество контролируемого процесса.

На рис. 2.1 представлены результаты анализа выборки (рис. 1.1), искусственно «засорённой» значением 350, которое находится за границами «усов».

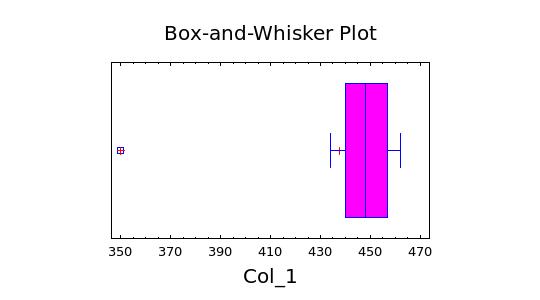
Рис.2.1. График Box-Whiskers для выборки (рис. 1.1), искусственно «засорённой» анормальным значением 350.

Это значение следует отбросить и повторить статистический анализ. Рис. 2.1 «перетащили» из системы STATGRAPHICS Plus for Windows , как это описано в конце предыдущего раздела.