8 Регрессионный анализ результатов совместных измерений для случая линейной модели
8.1. Цель занятия
Практическое освоение получения уравнения регрессии методом наименьших квадратов (МНК); оценки погрешностей параметров уравнения регрессии; проверки адекватности экспериментальных данных линейной модели; сравнения параметров двух уравнений регрессии.
8.2. Создание электронной таблицы с данными для статистического анализа.
Исходное положение: Рабочее окно системы STATGRAPHICS Plus for Windows. Для проведения регрессионного анализа результатов совместных измерений заполняем, как это описано в работе 1, две колонки (рис.8.1), (пример 8.1 [1]).
Рис. 8.1. Рабочее окно системы, подготовленное для регрессионного анализа
8.3. Статистический анализ
Статистическому анализу результатов совместных измерений обязательно предшествует графический анализ, то есть построение графика, в данном случае, ρ=f(T). Для этого последовательно щёлкаем левой кнопкой мыши на Plot (График ) / Scatterplots (Графики результатов измерений)/ X-Y Plot (График в координатах Y-X). В выпадающей таблице отмечаем, какие переменные откладываем по оси Y (в данном случае Сопротивление) и какие по оси X (Температура) и далее нажимаем кнопку OK.
Справа появляется вполне приличный график зависимости электросопротивления от температуры, который можно:
- растянуть на весь экран, щелкнув два раза левой кнопкой мыши;
- отредактировать, для чего щёлкнуть правой кнопкой мыши на поле графика и в выпавшем меню раскрыть Graphics Options (Операции с графиками);
- сохранить (записать) график (Save Graph) и затем вставить его при необходимости в отчёт (рис.8.2).
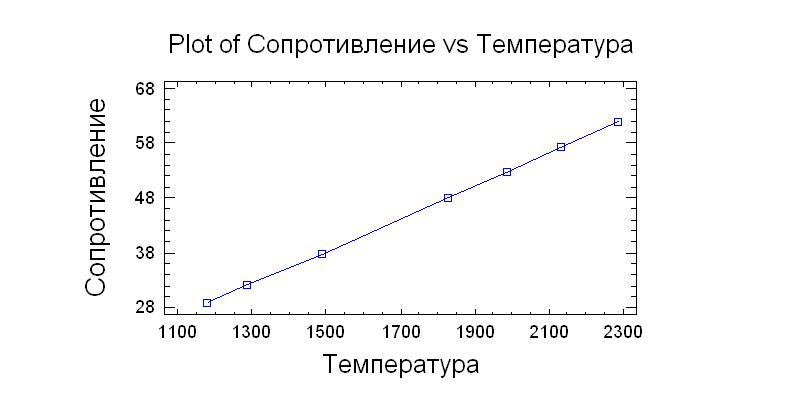
Рис. 8.2. Зависимость электросопротивления от температуры по данным рис.8.1
Видно, что зависимость ρ=f(T) близка к линейной, что в первом приближении позволяет оценить параметры линейной модели методом наименьших квадратов.
Для этого закрываем окно с графиком и последовательно щёлкаем левой кнопкой мыши по Relate (В данном контексте это выяснение отношений между зависимыми и независимыми переменными)/ Simple Regression (Простая регрессия). В данном случае речь идёт об однофакторной модели, которая может быть как линейной, так и более сложной. В выпадающей таблице отмечаем, какие переменные откладываем по оси Y (в данном случае Сопротивление) и какие по оси X (Температура) и далее нажимаем кнопку OK.
Слева появляется таблица с результатами регрессионного анализа и справа график зависимости ρ=f(T). Этот график отличается от ранее построенного (рис.8.2) тем, что вокруг линии регрессии нанесены границы доверительных интервалов ΔYi для Yi, вычисленные по уравнению 8.17 [1] для двух доверительных вероятностей 0,9 и 0,95. Поскольку они очень узкие, то они практически сливаются с линией регрессии и график здесь не приводится.
Теперь займёмся извлечением нужной информации из таблиц регрессионного анализа (Regression Analysis: - Linear model Y=a+b*X), для чего раскроем таблицу во весь экран двумя щелчками левой кнопкой мыши на поле таблицы (рис.8.3).Ниже названия таблицы раскрываются имена зависимой переменной Y (Dependent variable– Сопротивление) и независимой переменной – X (Independent variable – Температура). Латинские буквы a и b в уравнении регрессии на рис.8.3 соответствуют обозначениям коэффициентов регрессии b0 и b1 , принятым в ПЗ 8 [1].
В первом столбике
таблицы приведены определённые параметры
уравнения регрессии: b0–Intercept
(Пересечение) и b1
- Slope(Наклон);
во втором столбике их оценки (Estimate
b0
= - 6,31725 и
b1
= 0,0297636); в
третьем столбике корни
квадратные
из выборочных дисперсий
и
(формулы 8.7 и 8.8 в ПЗ 8 [1]) коэффициентов
регрессии b0
и b1
(Standard
Error
Sbo=0,393116
и Sb1=0,000220031;
в четвёртом столбике эмпирические
значения критерия Стьюдента (T-Statistic),
по значениям которых оценивают значимость
коэффициен -
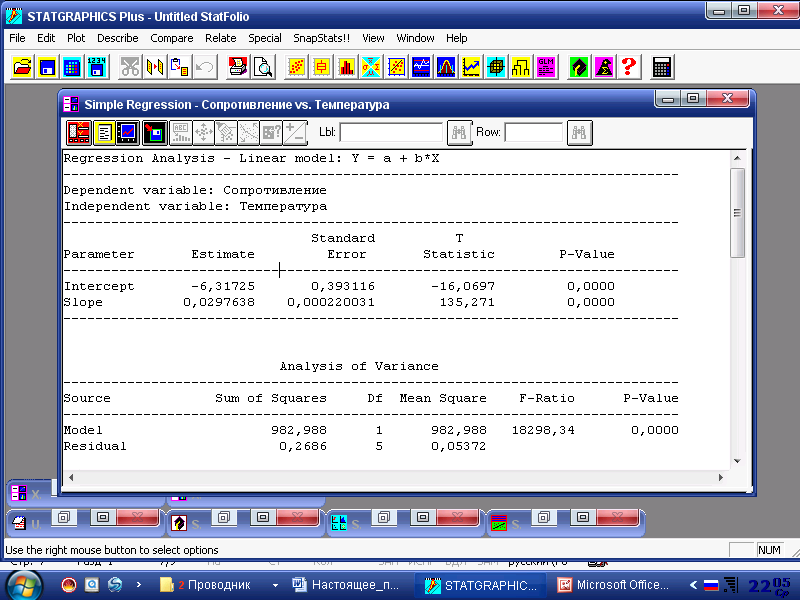
Рис. 8.3. Таблица с результатами регрессионного анализа зависимости ρ=f(T).
тов регрессии b0 и b1. Они существенно превосходят критическое значение критерия Стьюдента (t0,05;5=2,571), что свидетельствует о значимом отличие коэффициентов регрессии от нуля. Стоит также обратить внимание на цифры в пятом столбике P-Value (0,0000 и 0,0000), которые свидетельствуют о нулевой вероятности отсутствия связи между переменными (о значимости коэффициентов регрессии). Если какая-то из этих величин будет более 0,05, то это сигнал о незначимости соответствующего коэффициента регрессии.
Далее, зная значения Sbo=0,393116 и Sb1=0,000220031, оцениваем погрешности коэффициентов регрессии, как это описано в ПЗ 8 [1].
Собственно на этом заканчивается решение примера 8.1 из ПЗ 8 [1]: коэффициенты регрессии определены, их значимость доказана, погрешности коэффициентов регрессии также определены. Но таблица с результатами регрессионного анализа зависимости ρ=f(T) (рис. 8.3) содержит ещё много дополнительной информации, овладение которой требует более углублённого освоения регрессионного анализа [4].
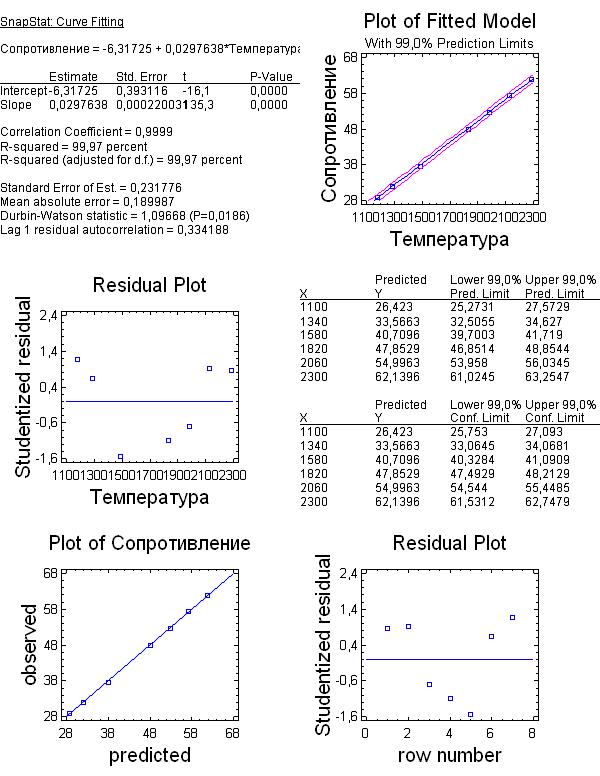
Рис. 8.4. Обобщённые данные регрессионного анализа модели ρ=f(T)
По мере освоения регрессионного анализа все вышеописанные шаги можно значительно сократить, получив при этом дополнительную информацию, в частности, о поведении остатков [4], что может служить графической проверкой адекватности линейной модели.
Для этого после создания электронной таблицы в системе STATGRAPHICS Plus for Windows (рис. 8.1) последовательно щёлкаем левой кнопкой мыши на SnapStats (Статистика)/ Curve Fitting (Эмпирическая кривая регрессии, положение которой определяется коэффициентами регрессии), в результате чего получаем обобщённую картину результатов регрессионного анализа (рис. 8.4.).