2.4.Методы измерений

Одну и ту же физическую величину можно измерить, используя совершенно разные методы измерения - приемы или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерений. Выбор конкретных методов измерения определяется решаемой измерительной задачей, заключающейся в определении физической величины с требуемой точностью в данных условиях измерений. Выбранный метод измерения, кроме того, должен учитывать ожидаемый размер измеряемой физической величины (очевидно, что измерить длину порядка 1 мм и 10⁸ км не одно и то же), быстроту процесса измерения (измерение температуры в нагревательной печи стационарной термопарой и измерение температуры движущейся по конвейеру заготовки контактной термопарой), возможное воздействие объекта измерений на результат измерения (охлаждение образца при образовании контакта с термопарой за счет теплоотвода через термоэлектроды). Естественно, что в ряде случаев на выбор метода измерений влияют и чисто финансовые соображения, объём предполагаемых измерений, квалификация исполнителей, потребность автоматизации процесса измерения.

Таблица 2.1. Метрологические характеристики средств измерений температур*

Средство измерений	Рабочий диапазон измерений, 0С	Допускаемая погрешность, 0C
1 Контактные термометры 1.1.Термометры расширения - стеклянный жидкостный термометр с несмачивающей жидкостью (ртуть) 1.2.Термоэлектрические термометры (термопары) - хромель - алюмель - платина-платина+10 % родия 1.3.Термометры сопротивления - платиновый термометр сопротивления	от - 60 до + 650 от - 270 до + 1300 от 0 до + 1600 от - 260 до + 1100	от 0,03 до 10 от 1,5 до 2,5 от 1,0 до 1,5 от 0,15 до 1,5
2.Пирометры излучения 2.1.Энергетические пирометры - яркостный квазимонохромати -ческий пирометр 2.2.Пирометры спектрального распределения (цветовые) - пирометр спектрального отношения	от 700 до 3000 от 800 до 2500	от 3,5 до 30 от 10 до 40
3.Специальные методы 3.1.Термочувствительные краски 3.2.Жидкие кристаллы	от 40 до 1350 от 30 до 250	от 2 до 65 -

*Примечание: В таблице приведены некоторые метрологические характеристики групп средств измерений, а не конкретных приборов.

В случае прямых измерений наиболее широко используются следующие основные методы: непосредственной оценки, сравнение с мерой, замещения, нулевой и дифференциальный (в порядке возрастания точности и чувствительности).

Метод непосредственной оценки является наиболее простым методом измерений и заключается в определении размера искомой физической величины непосредственно по отсчетному устройству измерительного прибора прямого действия. Например, измерение электросопротивления с помощью омметра, массы на циферблатных весах, измерение длины образца с помощью микрометра, измерение твёрдости методом Роквелла, силы электрического тока амперметром.

Наиболее многочисленной группой средств измерений, использующих этот метод, являются показывающие, в том числе и стрелочные приборы (амперметры, вольтметры, расходомеры). Этот же метод измерений реализуется в самопишущих приборах для измерения и контроля температуры, давления, концентраций. Измерения с помощью этого метода проводятся очень быстро, не требуют высокой квалификации операторов, но точность измерений чаще всего оказывается невысокой по сравнению с другими методами измерений.

Метод сравнения с мерой и его модификации обеспечивает более высокую точность и заключается в измерении искомой величины путем сравнения с величиной, воспроизводимой мерой. За результат измерения принимают значение равное значению меры. Например, измерение массы на рычажных весах с уравновешиванием гирями - мерами массы с известными значениями.

Метод замещения основан на сравнении с мерой, при котором измеряемую величину замещают известной величиной, воспроизводимой мерой. Метод замещения является разновидностью метода сравнения с мерой и широко используется, например, при точных измерениях электрического сопротивления в процессе нагрева (охлаждения) образца или при изучении фазовых превращений. В подобных случаях возникают затруднения, обусловленные необходимостью одновременно измерять ток и напряжение при одной и той же температуре (или одном и том же состоянии образца).

Если измерены значения тока I и падения напряжения U_R, то можно оценить величину электросопротивления образца по закону Ома R=U_R/I. Поскольку, измерения I и U_R занимают по меньшей мере несколько секунд, то и температура за это время изменится, а, следовательно, изменится сопротивление образца и ток в цепи. В конечном итоге, это приведет к появлению погрешностей в измерении R и неопределенности в оценке зависимости электросопротивления от температуры. Чтобы это устранить можно использовать метод замещения, электрическая схема которого приведена на рис.2.4.

Процесс измерения протекает следующим образом. Ключ К₂ находится в положении 1. При этом измеряют падение напряжения U на образце R_x (U=I_*R_x). С этой целью регулируют потенциометр до тех пор, пока гальванометр Г не установится на нуль. Эта процедура производится достаточно быстро, что позволяет одновременно измерить величину температуры T_I. Затем ключ К₂ переключают в положение 2 и снова устанавливают гальванометр на нуль, но на этот раз изменяя сопротивление R_N, в качестве которого используется калиброванный магазин сопротивлений. (Эту процедуру уже можно делать не спеша). Величина R_N в последнем случае равна сопротивлению R_x испытуемого образца при температуре T_I, т.к. в обоих случаях установка потенциометра соответствует одному и тому же напряжению U. При измерении падения напряжения на сопротивлении R_N, которое замещает неизвестное значение R_x, изменение R_x в условиях, например, переменных температур уже не играет никакой роли, т.к. оно в процессе настройки исключено из измерительной цепи и его значение не влияет на ток в цепи.

Рис.2.4. Схема измерения электросопротивления методом замещения.

Погрешность измерения R определяется в основном погрешностью потенциометра, точность которого обычно очень высока, и чувствительностью гальванометра, величиной тоже очень высокой, что в итоге дает малое значение R. Недостатком метода замещения является необходимость применения соответствующих многозначных мер (магазинов сопротивлений, емкостей, наборов гирь).

Нулевой метод является разновидностью метода сравнения с мерой, в котором результирующий эффект воздействия величин на прибор сравнения доводят до нуля.

Исторически нулевой метод является одним из первых в технике точных измерений. Взвешивание грузов на рычажных весах как равноплечих, так и неравноплечих, является наглядным и самым древним примером использования нулевого метода измерений. Классическим примером использования нулевого метода является измерение очень малых значений (<<1 Ом) электросопротивления с помощью двойного моста (рис.2.5).

Все сопротивления, участвующие в процессе измерения искомого значения Rx образуют три параллельные ветви: ABF; CDE и ACEF. Процесс измерения сводится к регулировке переменных сопротивлений R₁ и R₂ таким образом, чтобы гальванометр Г установился на ноль. Мост в этом случае уравновешен и тока между точками B и D не будет, а по ветви ABF пойдет ток равный току на линии CDE. Значения Rx тогда определяют как

R_x = R_N ( R₁/R₃),

где R₁ и R₂ >> R_N и R_x~R_N. При этих условиях неизвестное сопротивление R_x измеряют быстро и с очень высокой точностью (относительная погрешность может не превышать 0,05 %).

Другим примером использования нулевого метода является оптическая пирометрия - один из способов измерения высоких температур расплавов, газов или твердых тел.

Действие оптического пирометра заключается в следующем. Внутри зрительной трубы помещается электрическая лампа, нить накаливания которой находится в поле зрения оператора. Трубу наводят на объект измерения таким образом, чтобы все поле зрения было освещено объектом. Регулируя накал нити лампы, добиваются того, что яркость нити станет равной яркости объекта измерения. В этом случае нить сольется с фоном, как бы исчезнет (рис.2.6 а), температуры нити лампы и объекта измерения совпали. Накал нити регулируют силой тока, а амперметр градуируют в градусах температурной шкалы Цельсия.

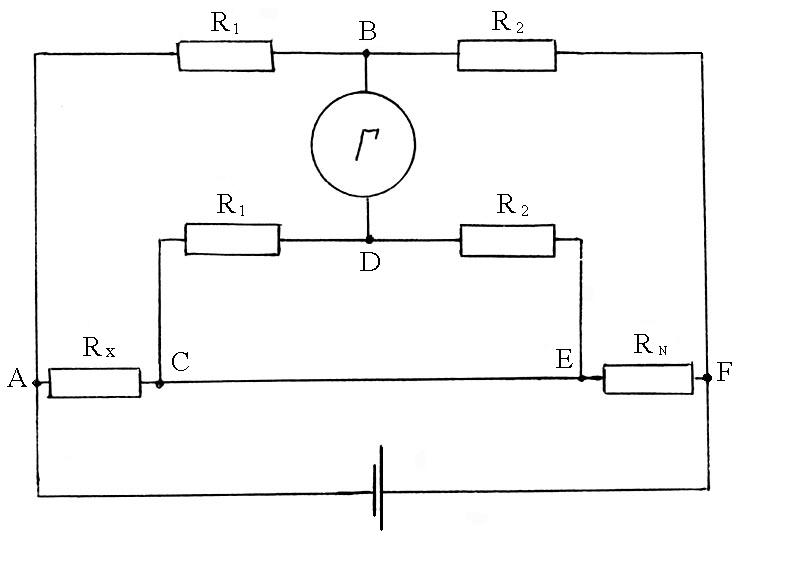
Рис. 2.5. Схема измерительного двойного моста.

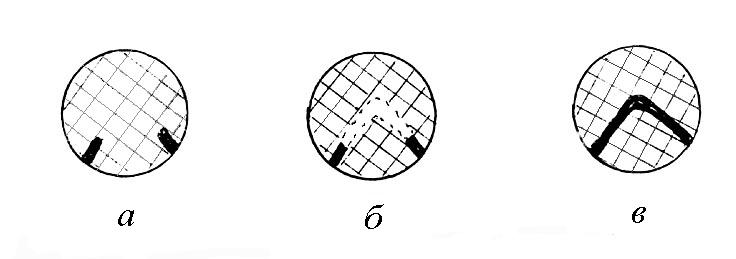
Рис. 2.6. Поле зрения оптического пирометра.

Если температура нити меньше температуры объекта, то она выглядит темнее фона (рис.2.6в), если же температура нити выше, то нить выглядит ярче фона (рис.2.6 б).

Дифференциальный (разностный) метод заключается в измерении разности между значениями измеряемой и известной (воспроизводимой мерой) величинами. Этот метод может быть использован, естественно, только тогда, когда просто и точно реализуется операция вычитания физических величин (длины, перемещения, электрические напряжения, ЭДС). Метод позволяет получить результаты измерений с высокой точностью даже при применении относительно грубых средств измерения для измерения разности. Осуществление метода возможно только при условии воспроизведения с большой точностью известной величины, значение которой близко к значению измеряемой. Это во многих случаях оказывается легче, чем изготовить средство измерения высокой точности для измерения физической величины, например, методом непосредственной оценки.

Рис. 2.7. Схема измерения длины дифференциальным методом.

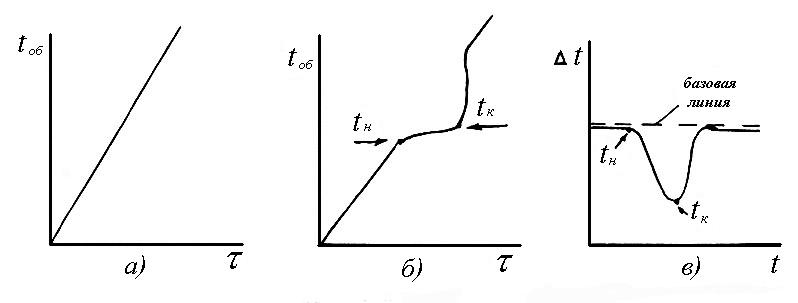
Рис. 2.8. Кривые нагрева при термическом (а и б) и дифференциальном (в) анализе.

На рис.2.7 показана схема измерения длины l_x дифференциальным методом. Рядом с объектом измерения помещена мера длины. Размер l меры известен с высокой точностью. Если измерить небольшую разность между длинами этих двух тел, то можно узнать длину объекта измерения l_x=l+a. (Здесь мы забежим несколько вперед и займемся оценкой относительной погрешности измерения l_x и a. Поскольку это понятие еще не рассматривалось, то к данному примеру следует вернуться после изучения раздела 2.6 Погрешности измерений).

Пусть погрешность измерения размера a не превышает некоторую величину a. Тогда результат измерения можно записать в виде a  a или а(1  a/a), где a/a - относительная погрешность измерения размера а.

Аналогичным способом оценим относительную погрешность измерения величины l_x. Результат измерения запишем как l_x=(l+a)a или l_x=(l+a)·(1+ a)/(l+a), где a/(l+a) - относительная погрешность измерения l_x. Здесь имеется в виду, что погрешность размера l (погрешность меры) много меньше, чем погрешность измерения размера a.

Так как l значительно больше a , то относительная погрешность измерения l_x значительно меньше относительной погрешности измерения a, т.е. (a/(l+a))a/a

Если, например, l=100 мм; a=1 мм и a/a=0,01 (или 1 %), то a/(l+a)~0,0001 (или 0,01 %), другими словами относительная погрешность измерения размера а на два порядка (!) меньше относительной погрешности измерения размера l_x. В этом примере значение l было определено с еще меньшей (чем 0,01%) погрешностью, что в принципе возможно при использовании в качестве меры плоскопараллельных концевых мер длины соответствующих классов точности.

Особенно просто дифференциальный метод может быть реализован в тех случаях, когда измеряемая разность физических величин (перемещения, температуры и т.д.) преобразуется в электрический сигнал.

Исключительно плодотворным является использование дифференциального метода измерений в физическом металловедении, в частности, он используется в дифференциальном термическом анализе и дифференциальной дилатометрии. Термический анализ и дилатометрия имеют такие большие заслуги перед материаловедением, что на них следует остановиться несколько подробнее.

Термический анализ и дифференциальный термический анализ. Термический анализ заключается в измерении температуры образца в функции времени при нагреве или охлаждении, расшифровке и интерпретации полученных кривых нагрева (охлаждения). В качестве измерительного преобразователя (см. раздел 2.5.3) при термическом анализе используется термопара, схема включения которой показана на рис.2.3.

Образец нагревается (охлаждается) с постоянной скоростью и температура образца регистрируется в функции времени (рис.2.8 а, б). Если в материале образца при нагреве (охлаждении) не происходит никаких превращений, связанных с изменением фазового состава или структуры, то температура образца возрастает по линейному закону (рис.2.8 а). При фазовых превращениях происходит выделение или поглощение скрытой теплоты превращения, а также наблюдаются изменения в теплоемкости материала. Поэтому при нагреве (охлаждении) с постоянной скоростью на кривой зависимости t=f(τ) могут появляться остановки, скачки или отклонения от линейной зависимости (рис.2.8 б). Температура t_н, при которой начинается отклонение, называется температурой начала превращения. Заканчивается превращение при температуре t_к. Таким образом, термический анализ предназначен главным образом для обнаружения и локализации по температурной шкале тепловых эффектов.

Основателем метода считают француза Ле-Шателье (H. Le Chatelier), опубликовавшего в 1887 году работу, в которой описал использование термопары для изучения термических свойств глины и минералов. Однако этот метод оказался мало чувствительным к небольшим тепловым эффектам, кривые нагрева сильно искажались при изменении скорости нагревания и зависели от параметров регистрирующего устройства. В 1899 году англичанин Робертс-Остен (W.C.Roberts-Austen) предложил использовать двухтермопарный метод, который с точки зрения метрологии является дифференциальным методом измерения, известным сейчас как дифференциальный термический анализ (ДТА).

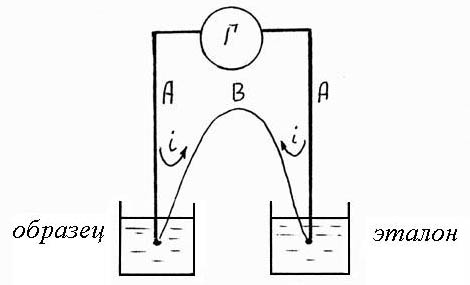
Рис.2.9. Схема включения дифференциальной термопары.

Схема включения термопар при ДТА показана на рис.2.9. Одна термопара размещается в образце, а другая в эталоне, термически инертном веществе, в котором в исследуемом температурном интервале не происходит никаких превращений. Регистрируемым параметром служит разность температур t образца t_об и эталона t_э (t = t_об - t_э). (Строго говоря, регистрируется не разность температур, а разность термо-ЭДС двух термопар включенных таким образом, что результирующая ЭДС в цепи является их разностью). Таким образом, ДТА действительно является разностным методом, т.к. фактически измеряется разность t температуры образца и температуры эталона, которая может быть представлена в виде функции температуры образца, эталона или нагревателя (рис.2.8 в).

Соединение термопар навстречу друг другу уже при незначительной разнице между t_о и t_эт приводит к появлению разности потенциалов, которая после усиления сигнала может быть легко зарегистрирована (рис.2.8 в). Повышенная чувствительность ДTA, характерная для дифференциальных методов вообще, позволяет исследовать образцы с малой маccой (вплоть до нескольких миллиграммов) или исключительно малые тепловые эффекты, например, взаимодействие примесей с дислокациями в металлах, радиационные повреждения полимерных материалов, теплота фазовых превращений и т.д.

Дифференциальная дилатометрия. Физический метод исследования, называемый дилатометрией (от лат. dilato - расширяю и греч. metreo - измеряю) состоит в измерении длины или объема образца в зависимости от температуры. Классическая дилатометрия обычно применяется в физическом металловедении для обнаружения изменения длины, вызванного различного рода фазовыми превращениями, а также для измерения термического коэффициента линейного расширения (ТКЛР) материалов. ТКЛР, как физическая величина, имеет огромное значение при инженерных расчетах точных (прецизионных) конструкций в машиностроении и приборостроении.

Измерительная аппаратура, применяемая в дилатометрии (так называемые дилатометры), относительно проста. Изменение длины l образца измеряется с помощью механического, оптического или электрического измерительного преобразователя и регистрируется в функции температуры при постоянной скорости нагрева (охлаждения). Регистрируемые кривые удлинения l=f(t) по крайней мере внешне напоминают кривые нагрева при термическом анализе (рис. 2.8 а, б). Площадки или отклонения от плавной кривой обусловлены изменением удельного объема при фазовых превращениях.

При дифференциальном дилатометрическом анализе рядом с образцом помещается эталон, в котором в исследуемом интервале температур не происходит никаких превращений, и измеряется разница в удлинениях образца и эталона в функции температуры.

Выбор эталонных материалов при проведении ДТА или дифференциального термического анализа определяется измерительной задачей. Если задачей измерения является измерение характеристик физических свойств (ТКЛР, теплоемкости, теплоты фазовых превращений), то в качестве материала эталонов следует выбирать материалы, свойства которых достоверно известны с высокой точностью. Например, при измерении ТКЛР в качестве эталонного материала используется специальный сплав пирос (82 % Ni; 7 % Cr; 5 % W; 3 % Fe; 3 % Mn) или плавленый кварц.

Если же задачей исследования является изучение превращений в сплаве при нагреве (охлаждении), то обычно в качестве эталонного материала можно использовать материал с близкими по отношению к изучаемому свойствами. Например, при изучении фазовых превращений в закаленных сталях и алюминиевых сплавах в качестве эталонов используют те же стали и алюминиевые сплавы, но в отожженном, равновесном состоянии.

Когда дилатометрические измерения проводят в относительно узком температурном интервале, температурную зависимость измеряемой ФВ можно описать линейной моделью:

l = l₀(1 + T) (2.4)

При дифференциальных измерениях можно попытаться вообще обойтись без эталона, как физического объекта. Для этого в качестве опорного сигнала следует использовать сигнал от термопары, измеряющей температуру образца, усиленный до величины, примерно равной сигналу от измерительного преобразователя. Включенные навстречу друг другу электрические сигналы от измерительного преобразователя и усиленный сигнал от термопары дадут горизонтальную базовую линию (рис. 2.9 в). Скорость нагрева в этом случае должна быть постоянной.