2.6. Погрешности измерений

2.6.1. Классификация погрешностей

Итогом измерения является результат измерения физической величины - значение величины, полученное путем ее измерения и выраженное в форме некоторого числа принятых для нее единиц. В металлофизическом эксперименте, как, впрочем, и в любом другом, почти невозможно представить себе измерения, результаты которых являлись бы истинными значениями измеряемой величины. Истинное значение физической величины - это значение ФВ, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующую физическую величину. Истинное значение ФВ есть понятие аналогичное понятию абсолютной истины и имеет более теоретическое значение, чем прикладное. В метрологии это понятие необходимо как теоретическая основа для раскрытия понятия погрешность измерений - отклонение результата измерения (x_изм) от истинного значения измеряемой величины (x_ист) и определяемое по формуле

x_изм = x_изм - x_ист , (2.6)

где x_изм - погрешность результата измерения.

В практической метрологии вместо истинного значения используется понятие действительное значение ФВ - значение ФВ, найденное экспериментальным путем и настолько близкое к истинному значению, что для поставленной измерительной задачи может его заменить. Действительным значением, например, является твёрдость образцовой меры или показание образцового средства измерения. В технических равноточных измерениях за действительное значение ФВ обычно принимают среднее арифметическое из серии последовательных независимых измерений.

В настоящее время вокруг терминов «истинное значение» и «действительное значение» идет оживленная дискуссия метрологов – теоретиков. Не вдаваясь в детали этих споров, ещё раз подчеркнём, что в данном пособии они используются для раскрытия понятия «погрешность»

Итак, результат измерения x_изм = x_дейст + x_изм практически всегда включает некоторую погрешность x_изм, которая и является главной головной болью всех, кто имеет дело с измерениями. Погрешности результатов измерений, или, короче, погрешности измерений, можно классифицировать по разным признакам.

По форме выражения различают абсолютные и относительные погрешности. Погрешность измерений, выраженная в единицах измеряемой величины, называется абсолютной погрешностью измерения. Например, при измерении длины образца получен ряд значений 20,22 мм, 20,25 мм, 19,98 мм при известном действительном размере 20,15 мм. Погрешности

L₁ = 20,22 мм - 20,15 мм = 0,07 мм,

L₂ = 20,25 мм - 20,15 мм = 0,10 мм,

L₃ = 19,98 мм - 20,15 мм = - 0,17 мм

являются абсолютными погрешностями соответственно первого, второго и третьего измерений.

Необходимо различать термины "абсолютная погрешность" и "абсолютное значение погрешности". Абсолютная погрешность может иметь как знак плюс, так и минус. Абсолютная погрешность по модулю, без учета знака, соответствует абсолютному значению погрешности. Абсолютная погрешность более информативна, т.к. содержит сведения не только о численном значении погрешности, но и о её знаке. Если, например, известен результат измерения x_изм и его абсолютная погрешность x_изм, то по (2.6) можно вычислить действительное значение ФВ x_действ. Абсолютное значение погрешности такой возможности не предоставляет.

Относительная погрешность выражается отношением абсолютного значения погрешности к действительному значению измеренной физической величины:

 = x_изм / x_действ .

На практике относительные погрешности чаще всего выражают в процентах ( = (x_изм / x_действ )100 %), иногда в промилле (от лат. pro mille - на тысячу), обозначаемых ‰. 1 ‰ = 0,001=0,1 %, т.е. 1 промилле в десять раз меньше процента.

Выражение погрешности в абсолютных или в относительных единицах зависит от контекста (от лат. contextus - соединение, связь), т.е. от описываемой измерительной ситуации. Абсолютные погрешности чаще используют при выражении и анализе близких по размеру физических величин, а относительные - при сравнении точности средств измерений, многозначных мер и т.д. Например, сравнивать точность методов измерения диаметра вала (d=50 мм; d=0,05 мм) и расстояния от Луны до Земли (l=380000 км; l=10 м), очевидно удобнее в относительных единицах.

По свойствам различают случайные погрешности, систематические погрешности и промахи. Деление погрешностей на случайные и систематические является наиболее важным классификационным признаком, т.к. их поведение и проявление различно, а методы обнаружения и их оценки требуют разного подхода.

Случайная погрешность изменяется случайным образом по знаку и значению в серии многократных измерений, проведенных с одинаковой тщательностью одного и того же размера физической величины. В появлении случайной погрешности не наблюдается каких-либо закономерностей. В качестве примера рассмотрим серию последовательных измерений некоторой ФВ, действительное значение которой известно и равно x_действ = 45. В результате измерений были получены следующие значения:46, 40, 49, 40, 42, 45, 48, 50, 40, 49, 41, 47. Абсолютные погрешности тогда выразятся рядом:1, -5, 4, -5, -3, 0, 3, 5, -3, 4, -4, 2. Построим зависимости значений средних, рассчитанных по 2,3,4...12 последовательным результатам измерений, и значений абсолютных погрешностей x_изм от номера измерений (рис. 2.13).

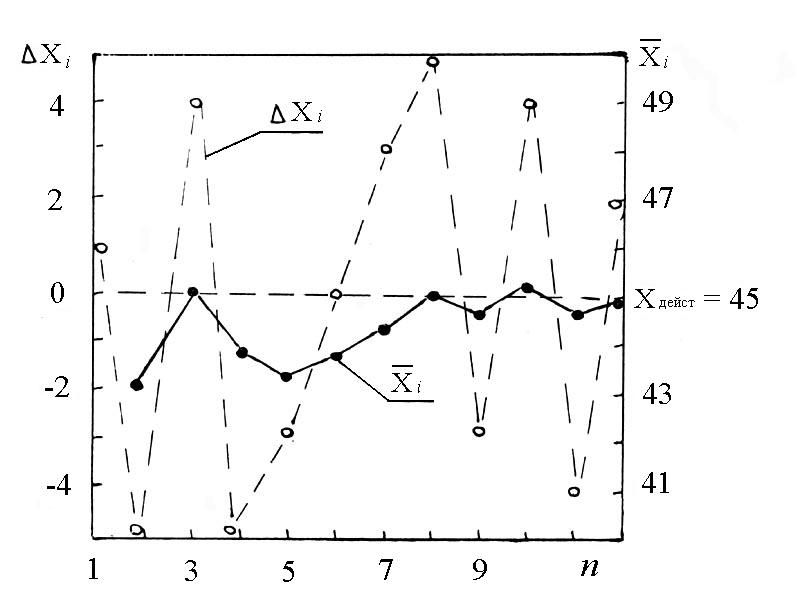
Рис. 2.13 График абсолютных погрешностей (∆x_i) последовательных измерений ФВ и средних значений (x_i) для двух, трех и так далее результатов измерений.

Из рисунка следует очень интересное и важное следствие: при увеличении числа измерений (в пределе n) среднее значение стремится к действительному значению, несмотря на возможное относительно большое рассеяние единичных результатов измерений относительно действительного значения ФВ. Но этот вывод справедлив только в том случае, если в появлении погрешностей не наблюдается какой-либо закономерности, т.е. все они действительно случайны. Если это так, то среднее значение при достаточно больших n может быть оценкой действительного значения ФВ.

Н аконец, обратим внимание на то, что отклонения последовательных средних в сериях измерений от действительного значения x_действ (см. рис. 2.13) значительно меньше, чем абсолютные погрешности отдельных результатов измерений. Пока запомним это обстоятельство.

П огрешности в любой сфере человеческой деятельности являются событиями неприятными. Но из всех погрешностей измерений случайные погрешности являются самыми безобидными, т.к. их относительно легко учесть методами математической статистики (см. главу 3).

Если погрешность результата измерения остается постоянной или закономерно изменяется при повторных измерениях одной и той же физической величины, то такую погрешность принято называть систематической погрешностью. Среднее значение последовательных отсчетов в этом случае отклоняется от известного действительного значения и продолжает отклоняться независимо от числа измерений, даже при n (рис. 2.14). Следует обратить внимание на то, что рассеяние единичных результатов измерений относительно среднего значения невелико, но разница между x_действ и средними в сериях остается постоянной (рис. 2.14,б). Средний результат измерения оказывается всё время_i смещенным относительно действительного значения измеряемой величины х_действ. В математической статистике (глава 3) оценки (статистики) - приближенные значения некоторых величин, полученные на основании результатов измерений или теоретических вычислений - содержащие систематические погрешности так и называются: смещенными оценками. При отсутствии систематической погрешности оценки называются несмещенными.

В метрологии результат измерения, содержащий систематические погрешности, называется неисправленным результатом, а сама систематическая погрешность - неисключенной. Неисправленные результаты или смещенные оценки результатов измерений имеют относительно низкую ценность, а иногда являются источником дезинформации. Поэтому проблема обнаружения и анализа систематических погрешностей является одной из главных задач метрологии.

Если известно действительное значение ФВ, то обнаружить систематическую погрешность не представляет труда, просто сравнивая х_действ и х_i. В металлофизическом эксперименте х_действ не известно практически никогда. Поэтому проблема обнаружения систематических погрешностей представляется исключительно сложной.

В главе 4 будут рассмотрены некоторые приемы обнаружения и исключения систематических погрешностей. Чтобы не заканчивать описание систематических погрешностей на пессимистической ноте, укажем на очень простой и достаточно эффективный способ обнаружения систематических погрешностей, который, к сожалению, ленятся применять почему-то даже экспериментаторы со стажем. Приём этот прост и с бородой - это графическое представление результатов измерений. При наличии прогрессивно возрастающей систематической погрешности (рис. 2.14,а), постоянной (рис. 2.14,6) или более сложной они достаточно ярко выявляются на графике последовательных измерений, правда, при этом надо правильно подобрать масштаб построения графика.

Промахи - измеренные значения ФВ, резко отличающиеся от общей совокупности данных. Источником этого типа погрешностей чаще всего является оператор, его невнимательность, усталость, неопытность. Например, при измерении угла вместо 35⁰32'20'' записано 45⁰32'20''. Очевидно, что при повторных измерениях оператор будет обращать больше внимания на отсчеты минут и секунд, оставляя неверными градусы.

Рис. 2.14 График результатов последовательных измерений ФВ, отягощенных