Прежде всего, изобразим все действующие в системе внешние силы и моменты, предполагая, что перемещение системы происходит в направлении действия силы f.
1. Рассчитаем перемещения всех тел системы, когда груз 6 переместится на ∆s6.
Очевидно, перемещение блока 1 также будет равно этой величине (нити нерастяжимы), т.е.
δs1 = δs6, (1)
а угол его поворота определяется соотношением
.
(2)
Угол поворота блока 4 вычисляется:
,
(3)
а угол поворота блока 3 аналогично определяется как
.
(4)
Угол поворота катка 2 (как подвижного блока) равен
(5)
а перемещение центра катка 2, равное перемещению груза 5 и деформации пружины,
(6)
2. Для решения задачи воспользуемся теоремой об изменении кинетической энергии системы материальных тел:
,
(7)
причем, поскольку
по условиям задачи движение системы
начинается из состояния покоя,
.
Вычислим вначале работу всех сил, действующих в системе.
Работа силы F, зависящей от перемещения, вычисляется:
.
(8)
Работа силы веса груза 6 равна
(9)
а работа силы трения этого груза
(10)
Работы сил веса катка 1 и блоков 3 и 4 не совершают работы, т.к. каток 1 перемещается по горизонтальной плоскости, а центры масс блоков 3 и 4 неподвижны. Работа момента М, приложенного к блоку 3, определяется:
(11)
Работа силы веса катка 2 равна
,
(12)
работа силы веса груза 5
,
(13)
а работа силы трения этого груза
.
(14)
Работа упругой силы пружины вычисляется по формуле
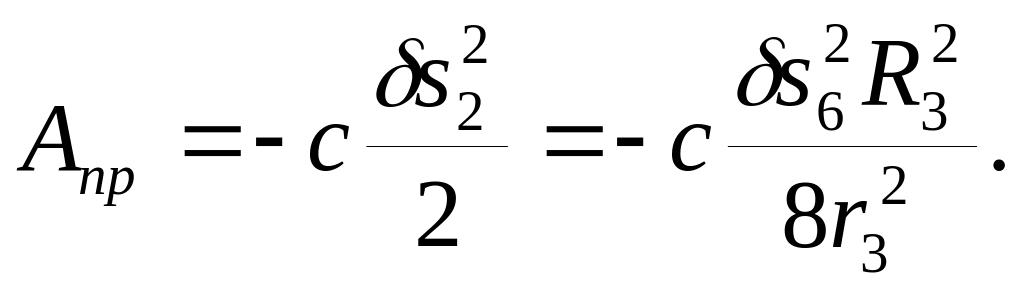(15)
Таким образом, сумма работ всех сил, действующих в системе, с учетом равенства δs6 = s1, в соответствии с (8)…(15) записывается:
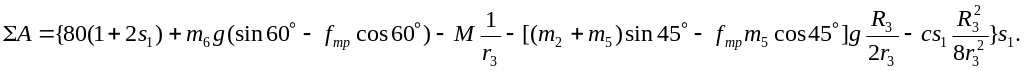(16)
Подставляя в (16) числовые данные задачи, получим
(17)
3. Для расчета кинетической энергии движущейся системы, выраженной через искомую скорость Vc2, выразим через эту скорость скорости перемещения (угловые скорости вращения) всех остальных тел согласно формулам (1)…(6).
(18)
Запишем теперь выражения для расчета кинетической энергии каждого из движущихся тел системы.
Каток 1 совершает плоско-параллельное движения, и в соответствии с теоремой Кенига его кинетическая энергия равна сумме энергий поступательного и вращательного движения катка:
(19)
где I1
– момент инерции катка, который для
однородного цилиндра равен
;
таким образом, в соответствии с (19), (18)
получаем:
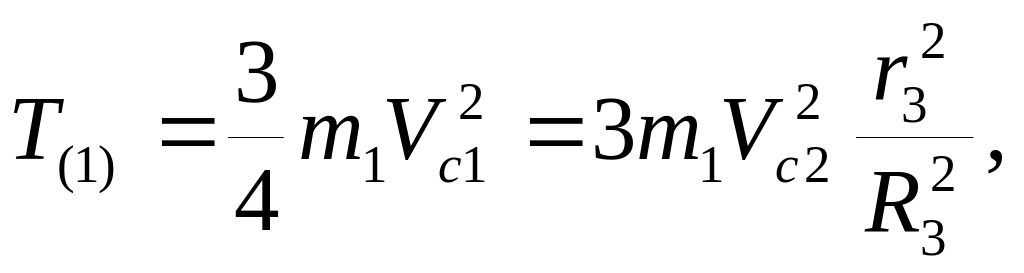(20)
причем не заданная
величина
в выражении для I1
(19) сокращается в силу (18).
Аналогично для катка 2 получаем:
(21)
Для ступенчатого
шкива 3 задан радиус инерции ρ,
поэтому момент инерции шкива вычисляется
по формуле
,
и для кинетической энергии этого тела,
совершающего вращательное движение, с
учетом (18) получаем формулу
(22)
У блока 4 масса
равномерно распределена по ободу,
поэтому
;
соотношение для вычисления кинетической
энергии этого блока принимает вид:
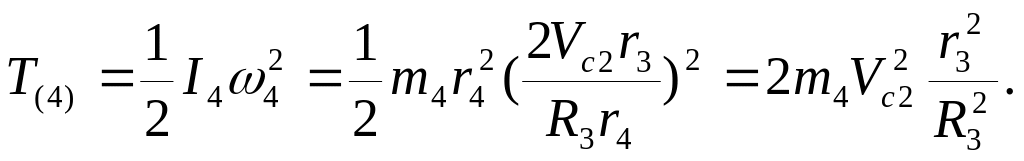(23)
Груз 5 совершает поступательное движение, его кинетическая энергия равна
(24)
Для груза 6 аналогично получаем
(25)
Значение суммарной кинетической энергии системы, входящее в выражение (7) , на основании (20)…(25) подсчитывается:
.
(26)
Подставляя в (25)
числовые данные задачи, получим
(27)
Подставляя (17) и (27) в (7), вычисляем искомую величину Vc2:
(28)
Задача Д- 3.
Механическая система (рис.1) состоит из однородных ступенчатых шкивов 1 (P1=15H) и 2 (P2=40H), грузов 3 (P3=50H), 4 (P4=10H), 5 (P5=30H), однородного катка 6 (P6=20H), а также невесомого блока 7. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М2 = 14Нм, приложенной к шкиву 2. Радиусы ступеней шкивов: R1 = 0,2м, r1 = 0,1м и R2 = 0,4м, r2 = 0,2м, их радиусы инерции 1 = 0,15м,2 = 0,3м.
Пренебрегая силами трения в системе, определить ускорение а3 груза 3.
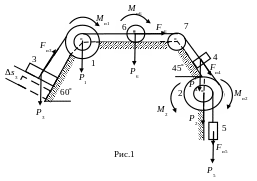
Решение.
Ускорение движения какого-либо тела, входящего в механическую систему, для которой известны действующие силы, удобно находить из общего уравнения динамики, т.к. именно в это уравнение непосредственно входят силы инерции, выражающиеся через ускорения тел.
Для того, чтобы воспользоваться общим уравнением динамики, прежде всего, изобразим все действующие в системе активные силы и моменты и силы инерции и моменты сил инерции (рис. 1).
Предположим, что перемещение системы происходит в направлении действия силы веса Р3.
1. Обозначим это перемещение δs3 и выразим перемещения всех остальных тел системы через эту величину, считая нити, связывающие тела, нерастяжимыми.
Очевидно, угол поворота шкива 1 определяется соотношением
.
(1)
Перемещение катка 6 вычисляется как
(2)
а угол поворота катка составит:
(3)
Перемещение груза 4, очевидно, равно перемещению катка 6
(4)
Угол поворота шкива 2 равен
(5)
а перемещение груза 5 определится по формуле
(6)
Зная перемещения и углы поворота всех тел, входящих в рассматриваемую систему, запишем для нее общее уравнение динамики:
(7)
Величины сил инерции и моментов сил инерции вычисляются следующим образом:
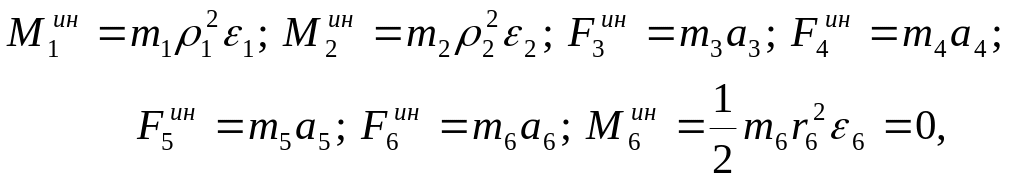(8)
где аi - линейные ускорения перемещения, а εi - угловые ускорения вращения i- тела, i = 1,2…6.
При вычислении
ускорений тел, входящих в систему,
заметим, что соотношения между их
линейными ускорениями аi,
угловыми ускорениями вращения εi
и линейным ускорением а3 груза
3 будут такими же, как соотношения (1)…(6)
между поступательными перемещениями
и углами поворота
тел системы и перемещением
груза 3, т.е.
,
(9)
Таким образом, общее уравнение динамики с учетом (1)…(6), (8) и (9) принимает вид:
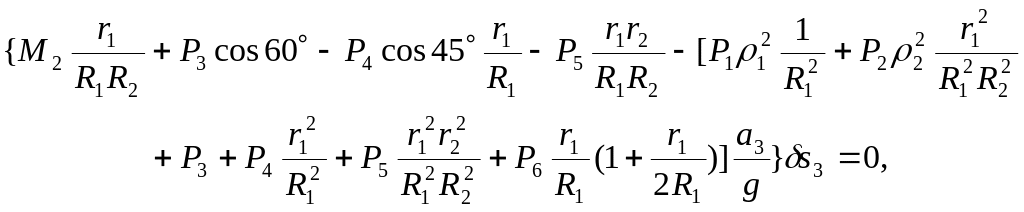(10)
откуда, после сокращения на получаем формулу для вычисления искомого ускорения груза 3
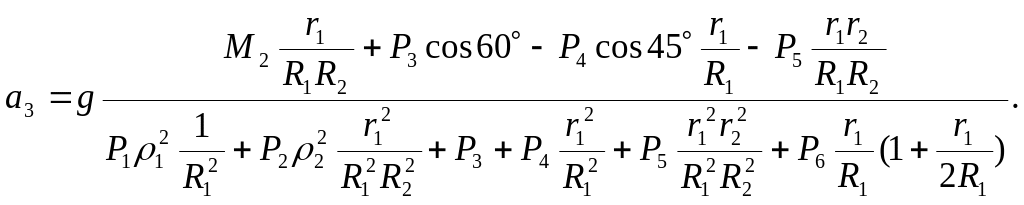(11)
Подстановка числовых данных задачи дает величину
а3 = 3,304м/с2.