Раздел 3. Динамика.

В разделе динамики предлагаются для решения три типовые задачи:

- задача Д-1 - на определение закона движения точки, совершающей вынужденные колебания при наличии сопротивления;

- задача Д-2 – на определение скорости движения тел с использованием теоремы об изменении кинетической энергии системы;

- задача Д-3 - на определение ускорения движения тел с использованием общего уравнения динамики или уравнения Лагранжа второго рода.

Задача Д-1.

Груз 1 массой m = 0,8 кг укреплён на пружинной подвеске в лифте 2 (жесткости пружин С₁ = 80 Н/м, С₂ = 120 Н/м, С₃ = 160 Н/м). Лифт движется вертикально по закону

z = a₁t² + a₂sint, (1)

где z направлена по вертикали вверх; величина z выражена в метрах, t – в секундах; а₁ = 9,81 м/с², а₂ = 0,2 м,  = 10 ¹/с.

На груз действует сила сопротивления среды R = v, где v – скорость груза по отношению к лифту, коэффициент сопротивления среды  = 8Нс/м. Вначале грузу сообщается скорость v₀ = 2м/с при нулевом начальном отклонении от положения статического равновесия груза.

Вес соединительной планки между пружинами и пружин не учитывается.

Найти закон движения груза по отношению к лифту.

Р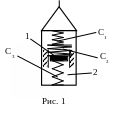 ешение.

Предложенная задача относится к задачам на составление и решение уравнения движения исследуемого тела. При этом по условию задачи требуется найти решения этого уравнения в движущейся системе координат, связанной с лифтом; закон движения лифта относительно неподвижной системы координат известен.

1. Решение задачи должно начинаться с замены заданной системы пружин одной эквивалентной пружиной.

Вначале заменим пружины 1 и 2 одной эквивалентной пружиной Э₁. Если вес груза, подвешенного к двум последовательно соединенным пружинам, равен mg, то под действием этой силы, одинаково действующей на обе пружины, пружины растянутся на длину

, , (2)

т.е. суммарное удлинение составит (3)

Эквивалентной пружиной Э₁, очевидно, считается такая, удлинение которой равно удлинению заменяемой системы при той же нагрузке. Таким образом,

, откуда , т.е.

. (4)

Заменяя теперь эквивалентной пружиной Э пружины Э₁ и 3, заметим, что удлинение пружины Э₁, очевидно, по величине равно укорочению пружины 3 и равно удлинению эквивалентной пружины Э, т.е.

,

причем, очевидно, , или , т.е.

,

и окончательно

. (5)

В данной задаче Н/м.

Отметим, что здесь рассмотрены два варианта комбинаций двух пружин – последовательное и встречное соединение. Для третьей возможной комбинации – параллельного соединения пружин С₁ и С₂ по аналогии легко получить формулу .

2. Получив новую схему задачи, изобразим ее на рис. 2. Выберем следующие оси координат Ось неподвижную z, которая входит в закон движения лифта (1), направим вертикально вверх. Закон движения груза ищется по отношению к лифту. Поэтому выберем связанную с лифтом ось х таким образом, чтобы ее начало находилось в положении статического равновесия груза, а направление совпадало бы с направлением действия силы веса этого груза.

В ыбор направления осей и начала отсчета на осях может быть произвольным, но предложенные здесь оси позволяют несколько упростить запись уравнений движения, что будет видно из хода решения задачи.

Изобразим на рис. 2 также действующие на груз силы.

Величина силы упругости пружины F_пр = С_э|∆l|. Направлена эта сила в сторону, противоположную отклонению ∆l. В данном случае ∆l = λ_СТ + х, причем, очевидно, С_э ∆l_СТ = mg.

Таким образом, проекция упругой силы на ось х равна

F_прх = - С_э (λ_СТ + х)= - (mg +C_э х). (6)

Величина силы сопротивления движению груза по условиям задачи определяется соотношением R = v, где v – скорость движения груза в данный момент времени, т.е. производная по времени от перемещения; . Направление силы сопротивления противоположно направлению скорости груза. Полагая в произвольный момент времени скорость, как и перемещение положительными, получаем, что проекция этой силы на ось х равна

(7)

Поскольку ищется уравнение относительного движения, в правую часть к действующим силам mg, F_пр, R необходимо добавить силу инерции переносного движения F_ин, полученную согласно закона движения лифта (1): и, следовательно, . С учетом противоположного направления оси х по отношению к оси z, получаем нужную нам проекцию:

. (8)

Уравнение движения груза в проекции на ось х записывается, с учетом (6)…(8):

(9)

при начальных условиях х(0)=0,

3. Для решения уравнения (9) представим его в канонической форме:

(10)

где . В данной задаче 2n = 8/0,8 = 10 1/c; k² = 208/0,8 = 260 1/с².

Решение неоднородного дифференциального уравнения (10) ищем в виде

,

где х_общ – общее решение однородного уравнения, соответствующего уравнению (10).

Решение однородного уравнения ищем способом подстановки Эйлера:

, т.е. ,

После сокращения на получаем характеристическое уравнение

.

В нашем случае корнями уравнения являются комплексные числа . Таким образом, общее решение однородного уравнения может быть представлено в виде

, (11)

где произвольные константы будут найдены в конце решения задачи из заданных начальных условий.

4. Частное решение уравнения (10) представляется в виде суммы двух решений: решения уравнения

(12)

и решения уравнения

. (13)

Для уравнения (12) решение очевидно:

, т.е. м . (14)

Решение уравнения (13) ищем в виде, соответствующем виду правой части:

(15)

Из (15) получаем:

(16)

Подставляя (15) и (16) в (13), получим, после раскрытия скобок в (14) и приведения подобных:

(17)

Для тождественного выполнения равенства (17) в любой момент времени необходимо и достаточно, чтобы множители при в левой и правой частях (17) были бы равны между собой, и также были бы равны между собой множители при в левой и правой частях. Таким образом получается система алгебраических уравнений для определения величин Р и β в выражении (15):

(18)

Система (18) легко решается:

; . (19)

Подставляя в (19) числовые данные задачи, получим Р = -0,106м, β = -0,559рад = -32°, т.е.

(20)

Окончательно решение уравнения (11) принимает вид

(21)

5. Для определения воспользуемся начальными условиями х(0) = 0,

Из (21) получаем

т.е. (22)

Дифференцируя (21) по времени и подставляя t = 0, получаем

или, с учетом (22), Аcosα = 0,1623. (23)

Из (22), (23) находим А = 0,1877, α = - 0,524рад = -30°.

Таким образом, искомое уравнение движения груза относительно лифта имеет вид:

. (24)

График x(t) представлен на рис. 3.

Задача Д- 2.

Механическая система (рис.1) состоит из сплошных однородных катков 1 (m₁=7кг) и 2 (m₂=4кг), ступенчатого шкива 3 (m₃=6кг) с радиусами ступеней R₃ = 0,3м, r₃ = 0,1м и радиусом инерции ₃ = 0,2м, блока 4 с массой m₄=5кг, равномерно распределённой по ободу, и грузов 5 (m₅=3кг) и 6 (m₆=8кг).

Коэффициент трения грузов о плоскости f_тр = 0,1. Тела соединены нитями, перекинутыми через блоки и намотанными на шкив 3; участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жёсткости с=80Н/м.

Система приходит в движение из состояния покоя под действием силы F = 120(1+4s), [s]=м, [F]=Н, зависящей от перемещения точки её приложения; s₀ = 0, в момент начала движения деформация пружины равна нулю. При движении на шкив 3 действует постоянный момент сил сопротивления М=1,2Нм.

Определить значение V_c2 в тот момент времени, когда перемещение s станет равным s₁ = 0,2м.

Р ешение.